
Översikt över pq-formeln
För att lösa givna uppgifter används pq-formeln för andragradsekvationer:

Denna formel används för att lösa en andragradsekvation av följande typ:
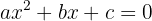 där
där 
Tillämpningen av denna metod är mycket enkel eftersom vi bara behöver sätta ekvationen lika med noll och sätta in värdena för a, b, c i pq-formeln.
Vid lösning av en andragradsekvation kan 3 saker inträffa:
- Det finns 2 värden för variabeln x som uppfyller ekvationen.
- Det finns en enda lösning.
- Lösningen tillhör inte mängden reella tal.
Övningsuppgifter för andragradsekvationer

1 Vi bestämmer värdena för a, b och c

2 Vi sätter in i abc-formeln och löser





3 Ekvationen har två olika reella lösningar


1 Vi bestämmer värdena för a, b och c

2 Vi sätter in i abc-formeln och löser





3 Ekvationen har två olika reella lösningar


1 Vi bestämmer värdena för a, b och c

2 Vi sätter in i abc-formeln och löser





3 Ekvationen har två olika reella lösningar

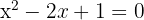
1 Vi bestämmer värdena för a, b och c

2 Vi sätter in i abc-formeln och löser


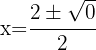


3 Ekvationen har endast en reell lösning


1 Vi bestämmer värdena för a, b och c

2 Vi sätter in i abc-formeln och löser




3 Ekvationen har ingen reell lösning.

1 Vi bestämmer värdena för a, b och c

2 Vi sätter in i abc-formeln och löser





3 Ekvationen har endast en reell lösning


1 Vi för över alla termer till ena sidan av ekvationen för att få följande form


2 Vi bestämmer värdena för a, b och c

3 Vi sätter in i abc-formeln och löser





4 Ekvationen har endast en reell lösning.


1 Vi utvecklar kvadraten av binomen

2 Vi för över alla termer till ena sidan och ordnar dem för att framställa ekvationen i följande form


3 Vi bestämmer värdena för a, b och c

4 Vi sätter in i abc-formeln och löser
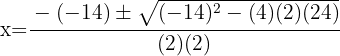




5 Ekvationen har två olika reella lösningar.


1 I detta fall kan vi förenkla genom att dividera båda sidor av ekvationen med 7

2 Vi bestämmer värdena för a, b och c

3 Vi sätter in i abc-formeln och löser





4 Ekvationen har två olika reella lösningar


1 Vi multiplicerar båda sidor med -1 för att få en ekvation med a > 0


2 Ekvationen har inga reella lösningar

1 Vi tillämpar distributiva lagen för att lösa upp parentesen och får:

2 Vi för över alla termer till vänstra sidan av ekvationen

3 Vi bestämmer värdena för a, b och c

4 Vi sätter in i abc-formeln och löser





5 Ekvationen har två reella lösningar.


1 Vi bestämmer värdena för a, b och c

2 Vi sätter in i abc-formeln och löser





3 Ekvationen har två olika reella lösningar
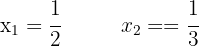

1 Vi utvecklar kvadraten av binomen

2 Vi för över alla termer till ena sidan och ordnar dem för att framställa ekvationen enligt följande


3 Vi dividerar båda sidor med 2 för förenkling

4 Vi bestämmer värdena för a, b och c

5 Vi sätter in i abc-formeln och löser





6 Ekvationen har två reella lösningar


1 Vi bestämmer värdena för a, b och c

2 Vi sätter in i abc-formeln och löser





3 Ekvationen har två olika reella lösningar


1 Vi bestämmer värdena för a, b och c

2 Vi sätter in i abc-formeln och löser





3 Ekvationen har två olika reella lösningar


1 Vi multiplicerar vänstra sidan av ekvationen med 6 och högra sidan av ekvationen med 2 för att eliminera nämnaren (6) och får därmed:

2 Vi bestämmer värdena för a, b och c

3 Vi sätter in i abc-formeln och löser





4 Ekvationen har två reella lösningar

Sammanfatta med AI:












