Kapitel

Första och andra binomiska formeln
Med den första och andra binomiska formeln beräknar man ett binom i kvadrat. Detta är lika med kvadraten av det första elementet, plus 2 gånger produkten av det första och andra elementet, plus kvadraten av det andra elementet.
När binomet i kvadrat innehåller en addition, är det dubbla av det första plus det andra elementet positivt.
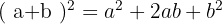
När binomet i kvadrat innehåller en subtraktion, är det dubbla av det första plus det andra elementet negativt.
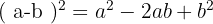
Räkneexempel: första och andra binomiska formeln
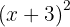
För att lösa denna ekvation använder vi den första formeln: Där sätter vi in 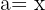 och
och  . Detta ger:
. Detta ger:
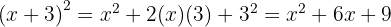
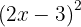
För att lösa denna ekvation använder vi den första formeln: Där sätter vi in 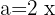 och
och  . Detta ger:
. Detta ger:


För att lösa denna ekvation använder vi den första formeln: Där sätter vi in 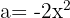 och
och  . Detta ger:
. Detta ger:
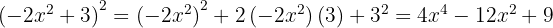
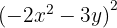
För att lösa denna ekvation använder vi den första formeln: Där sätter vi in 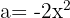 och
och  . Detta ger:
. Detta ger:
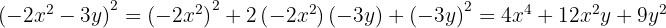

1 Det handlar om ett binom i kvadrat
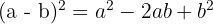
2 Hitta termerna för de enskilda elementen
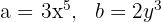
3 Sätt in dessa i motsvarande binomiska formel

4 Förenkla ekvationen
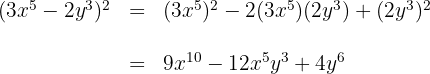
Tredje binomiska formeln
Produkten av en summa och en differens av två binomer är lika med differensen av respektive element i kvadrat. Denna beräknas med hjälp av den tredje binomiska formeln.

Räkneexempel: tredje binomiska formeln

Genom att använda formeln sätter vi in 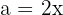 och
och 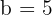 . Efter insättningen får vi:
. Efter insättningen får vi:
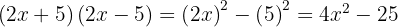 .
.

Genom att tillämpa formeln sätter vi in 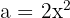 och
och 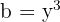 . Efter insättningen får vi:
. Efter insättningen får vi:
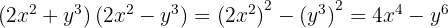 .
.
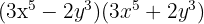
1 Det handlar om en produkt av en summa och en differens, som kan skrivas som differensen av de enskilda elementen i kvadrat.
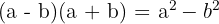
2 Hitta termerna för de enskilda elementen
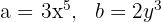
3 Sätt in dessa i den tredje binomiska formeln

4 Förenkla ekvationen
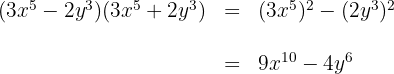
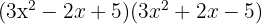
1 Det handlar om en produkt av en summa och en differens. För att kunna lösa denna delar vi upp de båda faktorerna

2 Tillämpa den tredje binomiska formeln
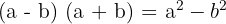
3 Hitta termerna för de enskilda elementen
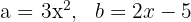
4 Sätt in dessa i den tredje binomiska formeln
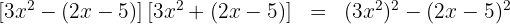
5 Lös den andra termen med hjälp av den andra binomiska formeln
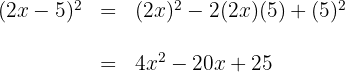
6 Sätt in resultatet i ekvationen och förenkla
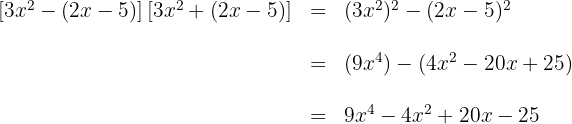
Binomiska summor och differenser av tredje graden
Ett binom av tredje graden, som består av en summa, löses med hjälp av följande formel:
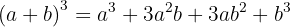
Ett binom av tredje graden, som består av en differens, löses med hjälp av följande formel:
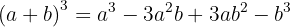
Räkneexempel: Binomiska summor och differenser av tredje graden
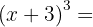
Vi sätter in  och
och  . Efter insättningen får vi:
. Efter insättningen får vi:
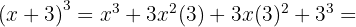
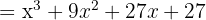 .
.


Vi sätter in 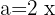 och
och 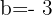 . Detta ger:
. Detta ger:
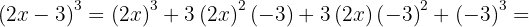
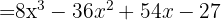
Här får man den binomiska formeln för en differens av tredje graden:
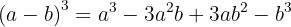

När vi tillämpar formeln för 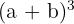 sätter vi in
sätter vi in 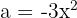 och
och 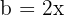 . Efter insättningen får vi:
. Efter insättningen får vi:
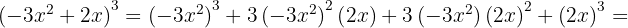
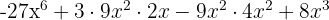
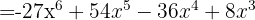
Här får man en tredje variant av formeln:
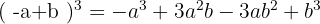
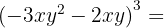
När vi tillämpar formeln för 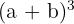 sätter vi in
sätter vi in 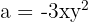 och
och 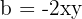 . Efter insättningen får vi:
. Efter insättningen får vi:
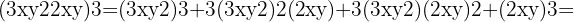
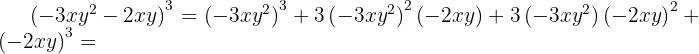
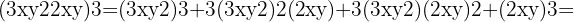
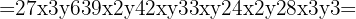
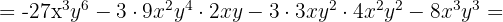
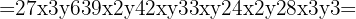
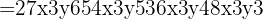
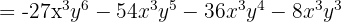
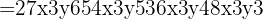
Detta ger en fjärde variant av formeln:
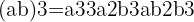
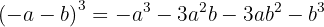
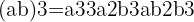
Trinom i kvadrat
Vid trinom i kvadrat skrivs de enskilda elementen om till en summa enligt följande regel: kvadraten av det första elementet plus kvadraten av det andra, plus kvadraten av det tredje, plus den dubbla produkten av det första och andra elementet, plus den dubbla produkten av det första och tredje elementet, plus den dubbla produkten av det andra och tredje elementet.

Räkneexempel: Trinom i kvadrat

För att lösa denna övning sätter vi in 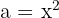 ,
, 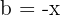 och
och  . När vi sätter in detta i formeln får vi:
. När vi sätter in detta i formeln får vi:
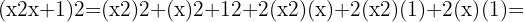
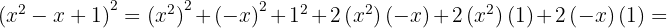
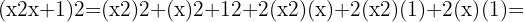
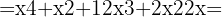
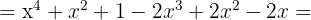
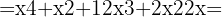
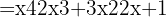
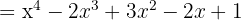
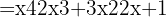
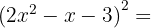
För att lösa denna övning sätter vi in 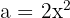 ,
, 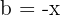 och
och 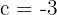 . När vi sätter in detta i formeln får vi:
. När vi sätter in detta i formeln får vi:
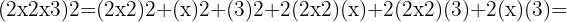
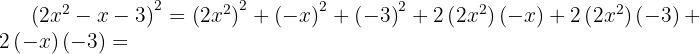
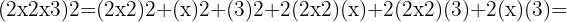
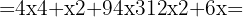
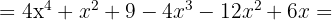
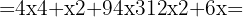
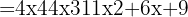
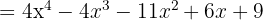
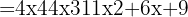

1 För att lösa trinomet i kvadrat, dela upp det i två enheter

2 Tillämpa den första binomiska formeln

3 Bestäm termerna för de enskilda elementen
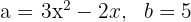
4 Sätt in dessa i den binomiska formeln
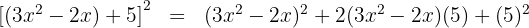
5 Lös den första termen med hjälp av den binomiska formeln
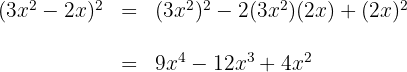
6 Sätt in resultatet i den föregående ekvationen och förenkla
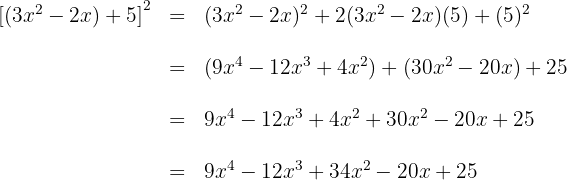
Faktorisering av binomer av tredje graden
I detta avsnitt skriver vi om ekvationerna till en produkt, det vill säga, vi faktoriserar dem.
Binomer av tredje graden faktoriseras på följande sätt:
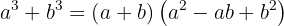
Räkneexempel: Faktorisering av binomiska summor av tredje graden
Faktorisera följande matematiska uttryck:
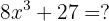
Ta först reda på hur du måste skriva om termerna så att formeln för faktorisering av binomiska summor av tredje graden kan tillämpas. I detta fall kan den skrivas om på följande sätt:
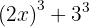
Genom att tillämpa formeln med 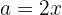 och
och  får man:
får man:
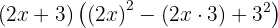
Förenkla så långt som möjligt:
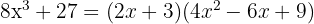
Räkneexempel: Faktorisering av binomiska differenser av tredje graden
Faktorisera följande matematiska uttryck:

Som i föregående exempel måste först bestämmas hur du måste skriva om termerna så att formeln för faktorisering av binomiska differenser av tredje graden kan tillämpas. I detta fall kan den skrivas om på följande sätt:
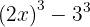
Genom att tillämpa formeln med 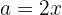 och
och  får man:
får man:
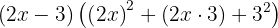
Förenkla så långt som möjligt:
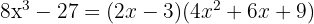
Binomprodukt med gemensam faktor
Vid en produkt av två binomer med en gemensam faktor är upplösningen möjlig på följande sätt:
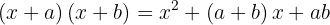
Räkneexempel: Binomprodukt med gemensam faktor
Förenkla följande ekvation:
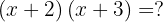
Här är användning av de binomiska formlerna inte nödvändig. Ekvationen kan lösas steg för steg med beaktande av förtecknen.
Multiplicera därför först termerna inom den första parentesen med dem i den andra:
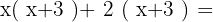
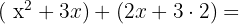
För att ekvationen ska förbli överskådlig och inget förtecken tolkas fel, är det vettigt att lösa upp parenteserna först helt i slutet. I detta fall sker ingen förändring av förtecken.
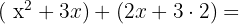
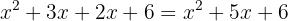
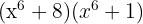
1 Här har vi återigen en binomprodukt med gemensam faktor

2 Bestäm värdena för variablerna från den binomiska formeln
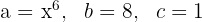 ,
,
3 Sätt in värdena i den aktuella ekvationen för binomprodukten med gemensam faktor

4 Förenkla termerna så långt som möjligt
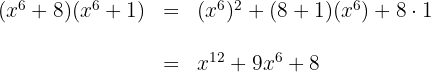
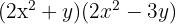
1 Här har vi återigen en binomprodukt med gemensam faktor

2 Bestäm värdena för variablerna från den binomiska formeln
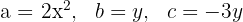
3 Sätt in värdena i den aktuella ekvationen för binomprodukten med gemensam faktor
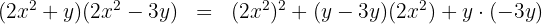
4 Förenkla termerna så långt som möjligt
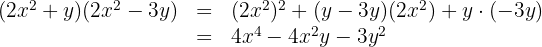
Sammanfatta med AI:












