y = 2
Framställ den konstanta funktionen:
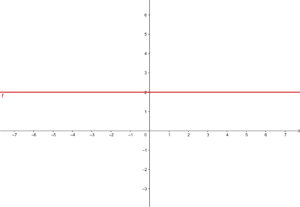
y = 2
Denna funktion avser alla punkter med koordinaterna (x,y), där y=2. Det vill säga, alla punkter (x,2), där x är en oberoende variabel som kan tilldelas ett godtyckligt värde. Till exempel (1,2) (-4,2) (5,2) etc.
y = –2
Framställ den konstanta funktionen:
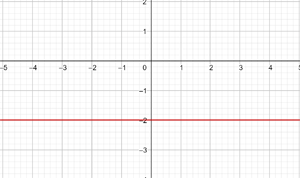
y = −2
Denna funktion avser alla punkter med koordinaterna (x,y), där y=-2. Det vill säga, alla punkter (x, -2), där x är en oberoende variabel som kan tilldelas ett godtyckligt värde. Till exempel (1,-2) (-4,-2) (5,-2) etc.
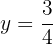
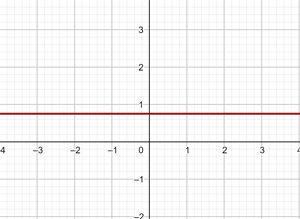
Framställ den konstanta funktionen:
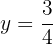
Denna funktion avser punkterna med koordinaterna (x,y), där 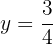 . Det vill säga, alla punkter
. Det vill säga, alla punkter 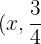 ), där x är en oberoende variabel som kan tilldelas ett godtyckligt värde. Till exempel:
), där x är en oberoende variabel som kan tilldelas ett godtyckligt värde. Till exempel:
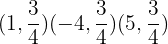
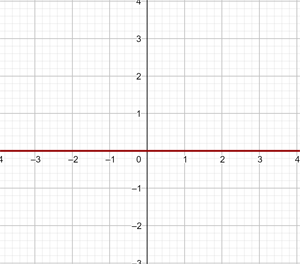
y = 0
Framställ den konstanta funktionen:
y = 0
Denna funktion avser punkterna med koordinaterna (x,y), där y=0. Det vill säga, alla punkter (x,0), där x är en oberoende variabel som kan tilldelas ett godtyckligt värde. Till exempel (1,0) (-4,0) (5,0) etc.
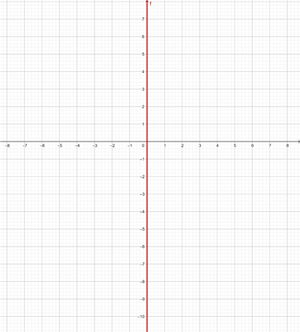
x = 0
Framställ den vertikala linjen:
x = 0
Detta är inte en funktion. Linjen avser alla punkter med koordinaterna (x,y), där x=0. Det vill säga, alla punkter (0,y), där y är en oberoende variabel som kan tilldelas ett godtyckligt värde. Till exempel (0,1) (0,-3) (0,5) etc.
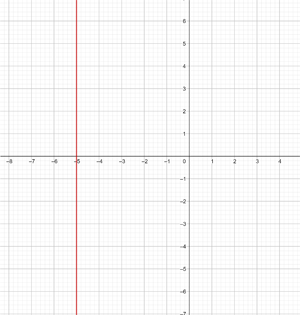
x = −5
Framställ den vertikala linjen:
x = −5
Denna funktion avser alla punkter med koordinaterna (x,y), där x=-5. Det vill säga, alla punkter (-5,y), där y är en oberoende variabel som kan tilldelas ett godtyckligt värde. Till exempel (-5,1) (-5,-3) (-5,5) etc.
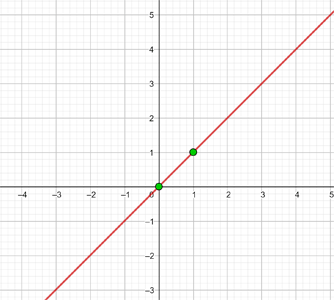
y = x
Framställ följande funktion: y=x
Denna funktion avser alla punkter med koordinaterna (x,y), där y=x. Det vill säga, alla punkter (x,y), där y=x är en oberoende variabel som kan tilldelas ett godtyckligt värde. Till exempel (1,1) (-3,-3) (5,5) etc.
För att möjliggöra en effektiv framställning skapar vi en tabell där vi på vänster sida för in värdena för x (vilket värde som helst) och på höger sida det värde som y antar efter utvärdering av x i vår funktion.

y = 2x
Framställ den linjära funktionen:
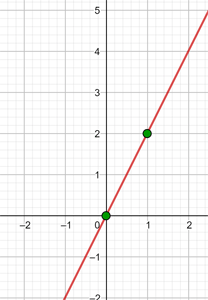
y = 2x
För att möjliggöra en effektiv framställning skapar vi en tabell där vi på vänster sida för in värdena för x (vilket värde som helst) och på höger sida det värde som y antar efter utvärdering av x i vår funktion.
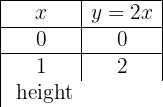
y = 2x − 1
Framställ funktionen:
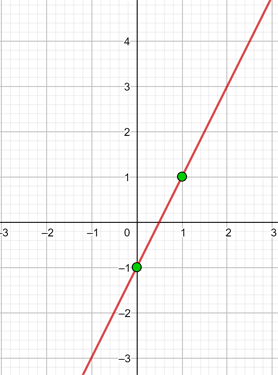
y = 2x − 1
För att möjliggöra en effektiv framställning skapar vi en tabell där vi på vänster sida för in värdena för x (vilket värde som helst) och på höger sida det värde som y antar efter utvärdering av x i vår funktion.
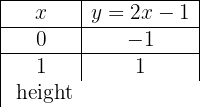
y = −2x − 1
Stelle die Funktion dar:
y = −2x − 1
Um eine effiziente Darstellung zu ermöglichen, erstellen wir eine Tabelle, in die wir auf der linken Seite die Werte von x (jeden beliebigen Wert) und auf der rechten Seite den Wert, den y nach der Auswertung des x in unserer Funktion zugewiesenen Wertes annimmt, eintragen.
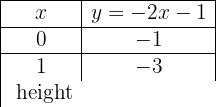
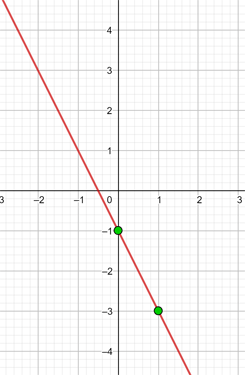
Framställ funktionen: 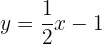
Framställ funktionen:

För att möjliggöra en effektiv framställning skapar vi en tabell där vi på vänster sida för in värdena för x (vilket värde som helst) och på höger sida det värde som y antar efter utvärdering av x i vår funktion.
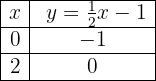
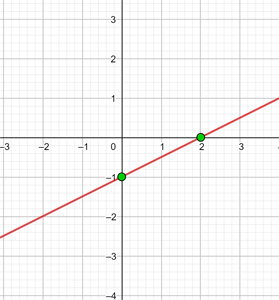
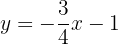
Framställ funktionen:
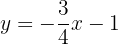
För att möjliggöra en effektiv framställning skapar vi en tabell där vi på vänster sida för in värdena för x (vilket värde som helst) och på höger sida det värde som y antar efter utvärdering av x i vår funktion.
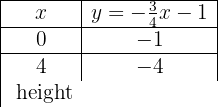
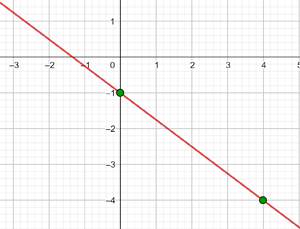
Funktionen har lutningen −3 och skär y-axeln vid −1.
Framställ följande funktion. Därvid är känt:
Funktionen har lutningen −3 och skär y-axeln vid −1.
y = -3x -1
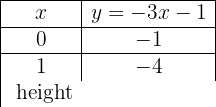
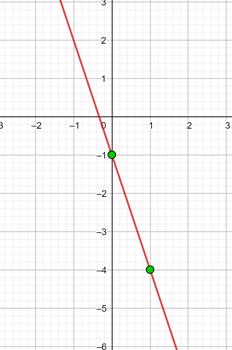
Funktionen har lutningen 4 och går genom punkten (−3, 2).
Funktionen har lutningen 4 och går genom punkten (−3, 2).
Funktionen har formen: y = mx + n
m = 4, vi sätter in värdet för m: y = 4x + n
En punkt är (−3, 2), vi sätter in värdena: 2 = 4 · (−3) + n n = 14
y = 4 x + 14

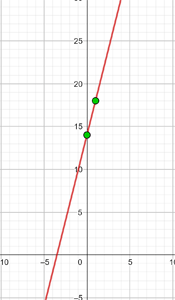
Går genom punkterna A(−1, 5) och B(3, 7).
Går genom punkterna A(−1, 5) och B(3, 7).
Funktionen har formen: y = mx + n
Går genom (−1, 5): 5 = −m + n
Går genom (3, 7) : 7 = 3m + n
Vi löser ekvationssystemet enligt följande:
−5 = m − n
7 = 3m + n
2 = 4m  m = ½ n = 11/2
m = ½ n = 11/2
Funktionen är: 

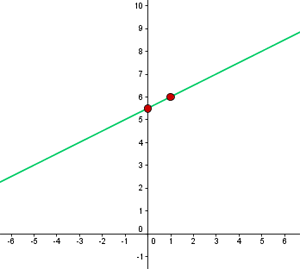
Går genom punkten P(2, −3) och är parallell med linjen med ekvationen y = −x + 7.
Går genom punkten P(2, −3) och är parallell med linjen med ekvationen y = −x + 7.
Funktionen är : y = mx + n
Två parallella linjer har samma lutning, m = –1
Går genom (2, −3):−3 = −1 · 2 + n n = − 1
Funktionen är : y = −x − 1
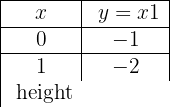
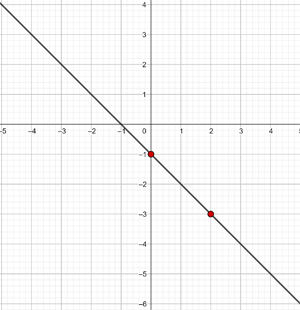
Under de första 10 veckorna av odlingen av en växt, som hade en storlek på 2 cm, konstaterades att dess tillväxt är direkt proportionell mot tiden, varvid växten var 2,5 cm stor under första veckan. Ställ upp en affin funktion som anger växtens höjd som funktion av tiden, och framställ den grafiskt.
Ursprunglig storlek = 2 cm
Veckovis tillväxt = 2,5 − 2 = 0,5
y = 0,5 x + 2
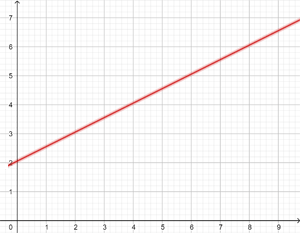
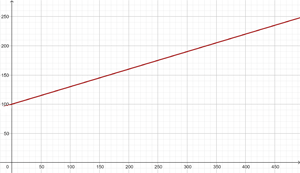
För en hyrbil debiteras dagligen 100 € plus 0,30 € per körd kilometer. Ställ upp ekvationen för linjen som förbinder de dagliga kostnaderna med antalet kilometer och framställ den grafiskt.
Om totalt 300 km körs under en dag, hur mycket måste då betalas?
y = 0,3 x + 100
y = 0,3 · 300 + 100 = 190 €
Beräkna koefficienterna för funktionen: f(x) = ax + b, om f(0) = 3 och f(1) = 4.
f(0) = 3
3 = a · 0 + b b = 3
f(1) = 4
4 = a · 1 + b a = 1
f(x) = x + 3
Sammanfatta med AI:

