Kapitel
Som vi vet kan derivator lösas på två sätt:
1. med hjälp av gränsvärdet med formeln
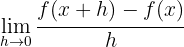
2. med hjälp av konkreta formler för varje enskilt fall. I denna artikel löser vi derivatoruppgifter genom det andra sättet.

Beräkna derivatorna av funktionerna
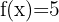
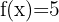
I detta fall använder vi formeln 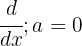 , som säger att derivatan av vilken konstant som helst är lika med noll.
, som säger att derivatan av vilken konstant som helst är lika med noll.



I det här fallet använder vi derivataregeln 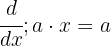 :
:
För en variabel som multipliceras med en konstant är derivatan lika med konstanten.

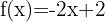
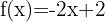
I det här fallet använder vi regeln 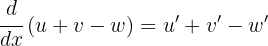 :
:
När man har en summa eller en differens av funktioner (eller algebraiska termer) är derivatan lika med summan och/eller differensen av derivatorna av varje enskild funktion (eller varje enskild algebraisk term).



I det här fallet måste varje algebraisk term deriveras.
För den första termen använder vi regeln 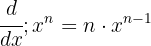 .
.



I det här fallet måste varje algebraisk term deriveras:
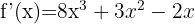
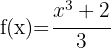
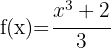
Här kan funktionen skrivas om:
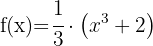
Derivatan är alltså  gånger derivatan av funktionen
gånger derivatan av funktionen 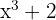
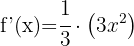

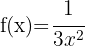
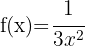
För den här typen av funktioner, där variabeln står i nämnaren, kan vi använda potensregeln:
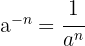
Vi kan alltså skriva om funktionen som:
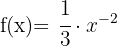
För derivatan använder vi formeln 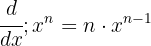
Vi får:
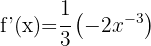



För att derivera en kvot använder vi formeln:

Derivatan blir då:
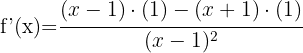

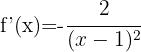


För att derivera en produkt använder vi formeln:
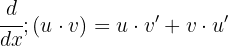
Derivatan blir då:
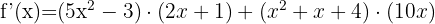
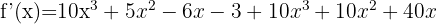
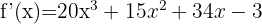
Beräkna med formeln för derivator av potenser
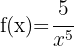
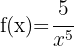
Tillämpa potensreglerna och skriv om funktionen:

Använd formeln för derivering av potenser:
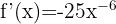
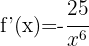
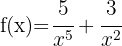
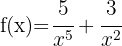
Tillämpa potensreglerna och skriv om funktionen:

Använd formeln för derivering av potenser:
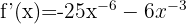



Tillämpa potensreglerna och skriv om funktionen:
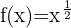
Använd formeln för derivering av potenser:


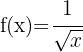
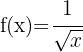
Tillämpa potensreglerna och skriv om funktionen:

Använd formeln för derivering av potenser:
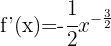
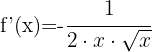


Tillämpa potensreglerna och skriv om funktionen:
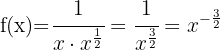
Använd formeln för derivering av potenser:
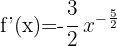
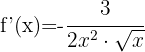
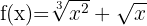
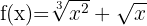
Tillämpa potensreglerna och skriv om funktionen:
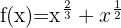
Använd formeln för derivering av potenser:
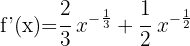
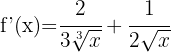
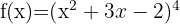
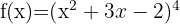
I detta exempel föreligger en funktion med en exponent. Tillämpa därför följande formel:
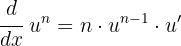

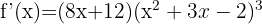
Beräkna med formeln för derivator av potenser
För att derivera funktioner som innehåller en rot kan vi först omvandla dem till potenser (som i föregående uppgift) eller använda följande formler för derivering:
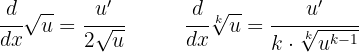


Eftersom det finns en kvadratrot kan vi använda den första formeln:
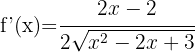
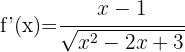


Eftersom rotexponenten är 4 använder vi den andra formeln:

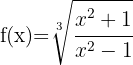
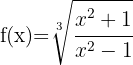
Eftersom rotexponenten är 3 använder vi den andra formeln.
Funktionen inuti roten kan deriveras med hjälp av kvotregeln:

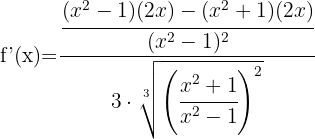
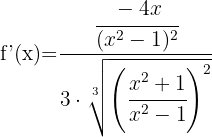
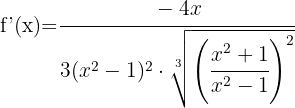
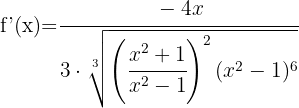
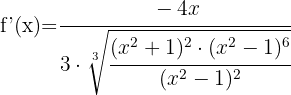
Vi förenklar uttrycket 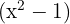 i täljare och nämnare i roten och löser på så sätt upp nämnaren. Vi får:
i täljare och nämnare i roten och löser på så sätt upp nämnaren. Vi får:
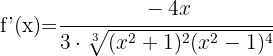

Derivera exponentialfunktionerna
I denna uppgift kommer vi att tillämpa följande formler:



Vi tillämpar den första formeln och får:
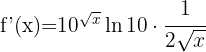
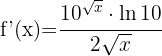
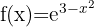
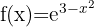
Vi tillämpar den första formeln och får:


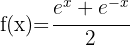
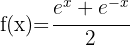
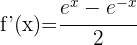
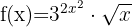
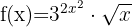
Vi tillämpar först regeln för produkter: 

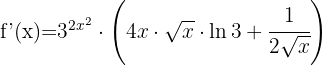
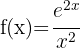
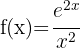
Vi tillämpar först regeln för produkter: 
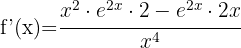
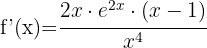

Beräkna derivatorna av logaritmfunktionerna
I denna uppgift används följande formler:
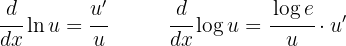
Dessutom kan vi tillämpa logaritmlagar för att få funktionen i en förenklad form och kunna derivera lättare:
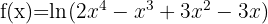
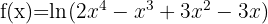
Tillämpa formeln för derivering av logaritmer:
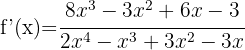


Tillämpa logaritmregeln 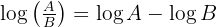 så får du:
så får du:

Derivera var och en av termerna med formeln för derivering av logaritmer:
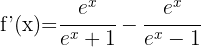
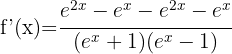
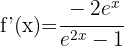


Tillämpa logaritmreglerna 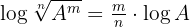 och
och 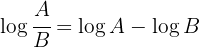 så får du:
så får du:

Tillämpa formeln för derivering av logaritmer:


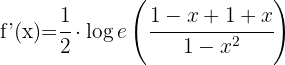
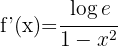
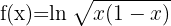
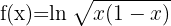
Tillämpa logaritmreglerna 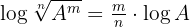 och
och 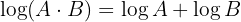 så får du:
så får du:
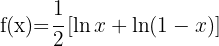
Tillämpa formeln för derivering av logaritmer:
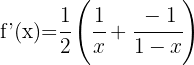
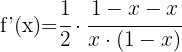
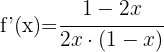
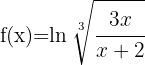
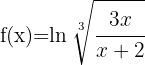
Tillämpa logaritmreglerna 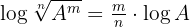 och
och 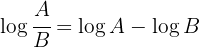 så får du:
så får du:

Tillämpa formeln för derivering av logaritmer: