Kapitel

Definition
I en exponentialfunktion tillordnas varje reellt värde av  en potens
en potens  . Därvid är
. Därvid är 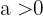 och
och  . Funktionen har formen:
. Funktionen har formen:

Talet  kallas också bas.
kallas också bas.
Grafiska framställningar av exponentialfunktioner
Hur beter sig exponentialfunktionen med avseende på sin bas?
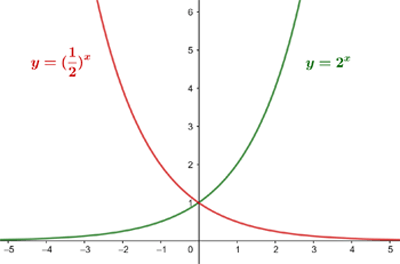
Vi skapar en värdetabell för funktionen 
| x | f(x) |
|---|---|
| -3 | 1/8 |
| -2 | 1/4 |
| -1 | 1/2 |
| 0 | 0 |
| 1 | 2 |
| 2 | 4 |
| 3 | 8 |
Vi ritar in grafen i koordinatsystemet
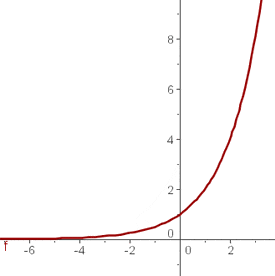
För jämförelse skapar vi en värdetabell för funktionen 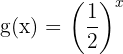
| x | g(x) |
|---|---|
| -3 | 8 |
| -2 | 4 |
| -1 | 2 |
| 0 | 0 |
| 1 | 1/2 |
| 2 | 1/4 |
| 3 | 1/8 |
Vi ritar in grafen i koordinatsystemet
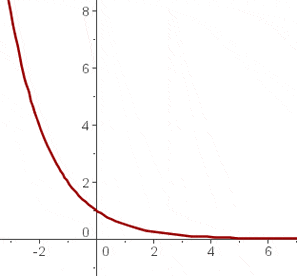
Man kan se att den första funktionen stiger konstant, medan den andra avtar konstant. Båda graferna är symmetriska med avseende på  -axeln
-axeln
Naturliga exponentialfunktionen
Den naturliga exponentialfunktionen (även kallad e-funktionen) har formen  . Därvid är
. Därvid är  fastställt genom
fastställt genom
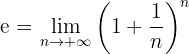 festgelegt.
festgelegt.
Denna skrivning introducerades omkring 1730 av Leonhard Euler, som forskade om talets egenskaper. Talet  är ett irrationellt tal. Dess första 10 decimaler är
är ett irrationellt tal. Dess första 10 decimaler är  .
.
Egenskaper hos e-funktionen
1 Definitionsmängd:  (reella positiva tal).
(reella positiva tal).
2 Värdemängd:  .
.
3 Funktionen är kontinuerlig.
4 Punkterna 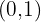 och
och 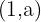 är del av grafen.
är del av grafen.
5 Funktionen är injektiv 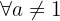 (ingen bild har mer än en urbild).
(ingen bild har mer än en urbild).
6 Funktionen är växande om 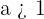 .
.
7 Funktionen är avtagande om 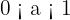 .
.
8 Funktionskurvorna  och
och 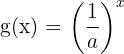 är symmetriska med avseende på
är symmetriska med avseende på  -axeln.
-axeln.
9 Exponentialfunktionen  med
med 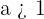 stiger snabbare än potensfunktionen
stiger snabbare än potensfunktionen  för varje värde av
för varje värde av 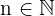 .
.
10 Exponentialfunktionen  har inversfunktionen
har inversfunktionen  . Inversfunktionen till e-funktionen är
. Inversfunktionen till e-funktionen är  .
.
Tillämpningsexempel av exponentialfunktionen
Exponentialfunktioner tillämpas inom en mängd arbetsområden, till exempel för beräkning av befolkningstillväxt och räntesatser.
Exponentiell tillväxt och avtagande
För att beskriva tillväxten av en befolkning används följande formel:

Funktionen 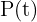 stiger exponentiellt och representerar befolkningens storlek vid tidpunkten
stiger exponentiellt och representerar befolkningens storlek vid tidpunkten  ;
;  är konstanten som anger tillväxten respektive avtagandet; om
är konstanten som anger tillväxten respektive avtagandet; om 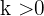 , kallas den tillväxtkonstant. Om
, kallas den tillväxtkonstant. Om 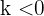 , benämner man den avtagandekonstant.
, benämner man den avtagandekonstant. 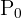 representerar den ursprungliga befolkningen vid tidpunkten för registreringens början:
representerar den ursprungliga befolkningen vid tidpunkten för registreringens början: 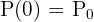 .
.
Den föregående formeln framställs med bas e-funktionen. I vissa fall kan den också uttryckas som en funktion med bas  : för detta tillämpas helt enkelt exponenternas egenskaper på
: för detta tillämpas helt enkelt exponenternas egenskaper på  och a uttrycks som
och a uttrycks som 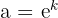 . Man får:
. Man får:
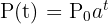
Exempel: En forskargrupp undersöker en bakteriekultur. Vid undersökningens starttidpunkt föreligger 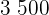 bakterier; en halvtimme senare redan
bakterier; en halvtimme senare redan 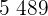 . Bestäm:
. Bestäm:
1 Antalet bakterier efter 2 timmar.
2 Antalet bakterier efter 3 timmar.
3 Den genomsnittliga ökningstakten av bakterieantalet under den andra timmen.
4 Den tid då bakterieantalet har fördubblats.
5 Den tid då bakterieantalet kommer att ligga på 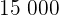 .
.
För att kunna lösa uppgifterna måste vi uttrycka tillväxtformeln  med
med 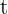 i minuter.
i minuter.
Vi känner redan till startvärdet 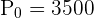 , men tillväxtkonstanten är fortfarande okänd. För att finna värdet av
, men tillväxtkonstanten är fortfarande okänd. För att finna värdet av  använder vi informationen från uppgiften
använder vi informationen från uppgiften 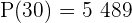 i tillväxtformeln:
i tillväxtformeln:
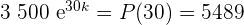
Vi dividerar båda sidorna med 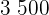 och tillämpar inversfunktionen till e-funktionen:
och tillämpar inversfunktionen till e-funktionen: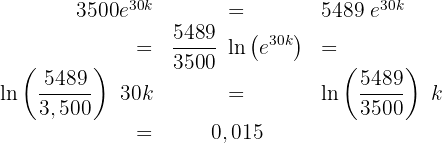
Funktionen som beskriver tillväxten av bakterieantalet är alltså:
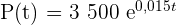
1 Antalet bakterier efter 2 timmar är:
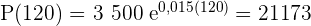
2 Antalet bakterier efter 3 timmar är:
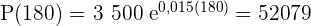
3 Den genomsnittliga ökningstakten av bakterieantalet under den andra timmen är:
Under den andra timmen av undersökningen, det vill säga mellan  och
och  , förändras bakterieantalet med
, förändras bakterieantalet med 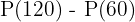 , därför är den genomsnittliga ökningen under denna tid
, därför är den genomsnittliga ökningen under denna tid
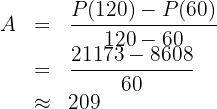
Bakterieantalet växer under den andra timmen av mätningen i genomsnitt med 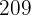 bakterier per minut.
bakterier per minut.
4 Den tid då bakterieantalet har fördubblats är:
Tillämpa följande ekvation:
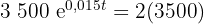
Vi dividerar båda sidorna med 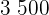 och tillämpar inversfunktionen till e-funktionen:
och tillämpar inversfunktionen till e-funktionen:
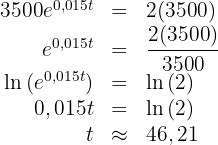
Bakterieantalet fördubblas alltså inom 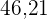 minuter.
minuter.
5 Den tid då bakterieantalet kommer att ligga på 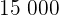 .
.
Tillämpa följande ekvation:
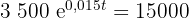
Vi dividerar båda sidorna med 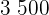 och tillämpar inversfunktionen till e-funktionen:
och tillämpar inversfunktionen till e-funktionen:
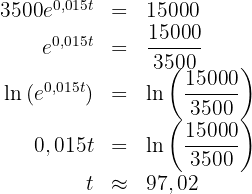
Bakterieantalet ligger efter 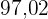 minuter på
minuter på 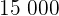 .
.
Ränta under året
Ett ursprungligt penningbelopp 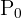 förräntas till en räntesats
förräntas till en räntesats  , som anges i decimaltal. Om räntan endast beräknas en gång, fås efter tillägg av räntan ett slutbelopp
, som anges i decimaltal. Om räntan endast beräknas en gång, fås efter tillägg av räntan ett slutbelopp  på
på
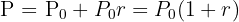
Om räntan beräknas flera gånger, beräknas utöver räntan över en viss tidsperiod ränta-på-ränta för nästa tidsperiod. Om den årliga räntesatsen är  och räntan beräknas
och räntan beräknas  gånger per år, har räntan efter
gånger per år, har räntan efter  år beräknats
år beräknats 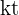 gånger och det nya slutbeloppet är
gånger och det nya slutbeloppet är

Exempel: 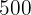 placeras till en årlig räntesats på
placeras till en årlig räntesats på 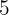 . Hur högt är tillgodohavandet efter
. Hur högt är tillgodohavandet efter  år, om räntan beräknas tre gånger årligen?
år, om räntan beräknas tre gånger årligen?
För att beräkna tillgodohavandet efter  år vid en trebonadsränta per år har vi följande värden:
år vid en trebonadsränta per år har vi följande värden: 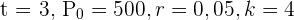 .
.
Sätt in värdena i formeln:
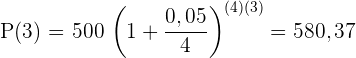
Efter  år ligger tillgodohavandet på
år ligger tillgodohavandet på 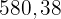
Kontinuerlig ränta
För att bestämma slutvärdet av en investering efter  år med kontinuerlig ränta, det vill säga när räntan inte ska beräknas månadsvis, dagligen eller årligen, utan kontinuerligt, använder vi följande formel:
år med kontinuerlig ränta, det vill säga när räntan inte ska beräknas månadsvis, dagligen eller årligen, utan kontinuerligt, använder vi följande formel:

Exempel: 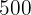 placeras till en årlig räntesats på
placeras till en årlig räntesats på 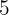 . Hur högt är tillgodohavandet efter
. Hur högt är tillgodohavandet efter  år, om räntan beräknas kontinuerligt?
år, om räntan beräknas kontinuerligt?
För att bestämma tillgodohavandet efter  år vid kontinuerlig ränta använder vi värdena
år vid kontinuerlig ränta använder vi värdena 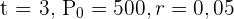 .
.
Sätt in värdena i formeln:
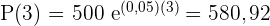
Efter  år ligger tillgodohavandet på
år ligger tillgodohavandet på 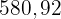 och är den övre gränsen för möjligt tillgodohavande.
och är den övre gränsen för möjligt tillgodohavande.
Sammanfatta med AI:












