
Vad är oändligheten och hur löser man uppgifter med gränsvärden?
När vi har att göra med gränsvärden måste vi känna till begreppet oändlighet. Observera att oändligheten inte representerar ett specifikt tal. I vissa fall kommer vi att behandla det som ett tal för att hitta gränsvärden, men vi måste ändå ha i åtanke att oändligheten i många fall inte beter sig som ett normalt tal.
Det finns fall där räkneoperationer med oändligheten är obestämda. Då beter sig  inte som ett tal. Vid dessa obestämda räkneoperationer måste vi ändra funktionen vars gränsvärde vi vill beräkna något, så att det inte längre finns någon obestämd funktion. Förfarandet kallas också ”elementär omformning”.
inte som ett tal. Vid dessa obestämda räkneoperationer måste vi ändra funktionen vars gränsvärde vi vill beräkna något, så att det inte längre finns någon obestämd funktion. Förfarandet kallas också ”elementär omformning”.
Epsilon-delta-kriteriet för gränsvärden säger:
Gränsdefinition: Uppgifter
Undersök med hjälp av epsilon–delta-kriteriet:
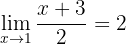
Vi betraktar ett godtyckligt värde för 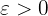 . Att bevisa är att ett
. Att bevisa är att ett 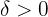 existerar som uppfyller definitionen av gränsvärdet.
existerar som uppfyller definitionen av gränsvärdet.
Med
(ännu okänt) måste det vara uppfyllt att:
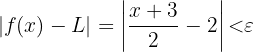
Genom förenkling får vi:
Försök att få 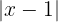 på ena sidan av olikheten för att erhålla ett uttryck för
på ena sidan av olikheten för att erhålla ett uttryck för 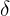 . Genom att multiplicera båda sidor av olikheten med 2 får vi:
. Genom att multiplicera båda sidor av olikheten med 2 får vi:
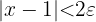
För 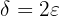 går alltså olikheten upp. Därmed är det begärda beviset fört.
går alltså olikheten upp. Därmed är det begärda beviset fört.
Vad betyder detta egentligen?
Det betyder att för varje värde av 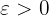 som vi betraktar kan vi hitta ett värde
som vi betraktar kan vi hitta ett värde 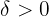 som uppfyller definitionen, eftersom vi för detta har ställt upp formeln (i detta fall
som uppfyller definitionen, eftersom vi för detta har ställt upp formeln (i detta fall 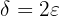 ).
).
Om till exempel 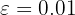 vore givet, skulle vi få
vore givet, skulle vi få 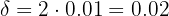 . Därför skulle vara lika med
. Därför skulle vara lika med
 .
.
D.v.s. 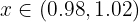 . För varje godtyckligt värde
. För varje godtyckligt värde  i intervallet
i intervallet 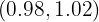 skulle det gälla:
skulle det gälla:
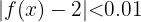
T.ex. skulle för 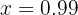 vara
vara 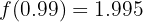 . Följaktligen:
. Följaktligen:
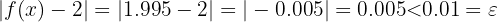
Likaså skulle för 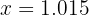 vara
vara 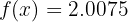 . Följaktligen:
. Följaktligen:
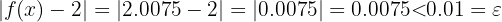
Betrakta grafen till funktionen  och ange de sökta gränsvärdena:
och ange de sökta gränsvärdena:
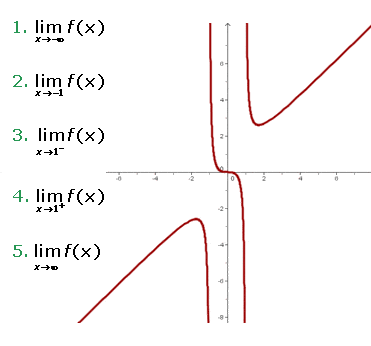

Funktionsgrafen i koordinatsystemet
Funktionsgrafen för gränsvärdena
1 Det första sökta gränsvärdet är
När 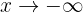 , det vill säga när
, det vill säga när  minskar mot oändligheten, faller även funktionen obegränsat. Följaktligen:
minskar mot oändligheten, faller även funktionen obegränsat. Följaktligen:
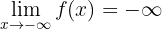
2 Bestäm nu
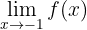
Vi kan observera att funktionen minskar mot oändligheten när  närmar sig
närmar sig  från vänster. När
från vänster. När  närmar sig
närmar sig  från höger ökar däremot funktionen mot oändligheten. Därför kan vi dra slutsatsen att inget gränsvärde existerar.
från höger ökar däremot funktionen mot oändligheten. Därför kan vi dra slutsatsen att inget gränsvärde existerar.
3 Beräkna nu
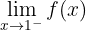
Här betraktas det vänstersidiga gränsvärdet. Vi kan observera att funktionen minskar mot oändligheten när  närmar sig
närmar sig  från vänster. Gränsvärdet är alltså:
från vänster. Gränsvärdet är alltså:
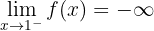
4 Det fjärde gränsvärdet är

Här betraktas det högersidiga gränsvärdet. Följaktligen:
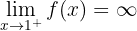
5 Slutligen, bestäm gränsvärdet

Detta liknar mycket det första exemplet. Man kan observera att  ökar mot oändligheten.
ökar mot oändligheten.  ökar också mot oändligheten. Följaktligen:
ökar också mot oändligheten. Följaktligen:
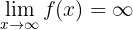
Beräkna gränsvärdet:

Sök gränsvärdet:
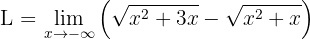
När vi betraktar gränsvärdet mot minus oändligheten får vi en obestämd form:
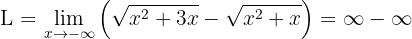
Eftersom värdet av  är obestämt, måste vi omforma funktionen algebraiskt.
är obestämt, måste vi omforma funktionen algebraiskt.
Innan vi börjar med den algebraiska omformningen kan vi skriva om gränsvärdet med dess egenskaper:
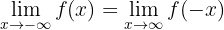
Gränsvärdet blir alltså:
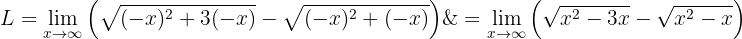
För att ta bort subtraktionen med oändlighet rationaliserar vi uttrycket (d.v.s. multiplicerar och dividerar med det konjugerade):
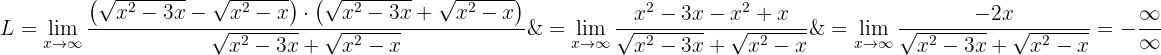
När vi tittar på funktionens globala beteende, det vill säga dess beteende mot oändligheten, får vi återigen en obestämd form 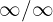 . För att ta bort denna obestämdhet multiplicerar och dividerar vi med
. För att ta bort denna obestämdhet multiplicerar och dividerar vi med 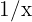 :
:
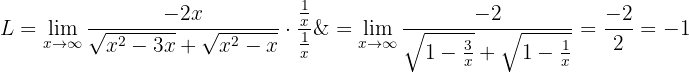
Vi har alltså fått det sökta resultatet:
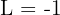
Beräkna gränsvärdet:
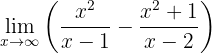
Sök gränsvärdet:

När vi betraktar gränsvärdet mot oändligheten får vi:
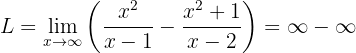
För att omvandla det obestämda uttrycket kan vi här skriva om bråken med gemensam nämnare:
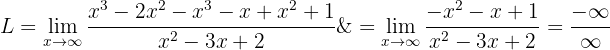
Nu har vi det obestämda uttrycket 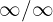 . Vi kan ta bort det genom att multiplicera och dividera med en lämplig term, nämligen monomet av högsta grad i täljaren eller nämnaren, här
. Vi kan ta bort det genom att multiplicera och dividera med en lämplig term, nämligen monomet av högsta grad i täljaren eller nämnaren, här 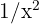 :
:
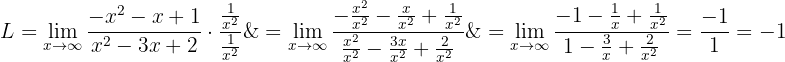
Gränsvärdet är alltså:
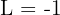
Beräkna gränsvärdet:

När vi betraktar gränsvärdet mot oändligheten får vi:
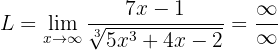
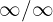 är ett obestämt uttryck. Vi omformar därför igen genom att multiplicera och dividera med monomet av högsta grad (i täljaren eller nämnaren). I detta fall tar vi
är ett obestämt uttryck. Vi omformar därför igen genom att multiplicera och dividera med monomet av högsta grad (i täljaren eller nämnaren). I detta fall tar vi 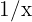 — eftersom nämnaren innehåller en tredjegradens rot kan "monomet"
— eftersom nämnaren innehåller en tredjegradens rot kan "monomet"  ses som ett monom av första graden. Vi får:
ses som ett monom av första graden. Vi får:
När vi tar gränsvärdet mot oändligheten får vi:

Beräkna gränsvärdet:
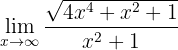
När vi betraktar funktionen mot oändligheten får vi:

Eftersom uttrycket är obestämt omformar vi igen genom att multiplicera och dividera med monomet av högsta grad ( ; observera att potenserna i täljaren delas med 2 eftersom de ligger under ett kvadratrotsuttryck):
; observera att potenserna i täljaren delas med 2 eftersom de ligger under ett kvadratrotsuttryck):
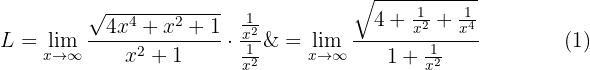
När vi tar gränsvärdet mot oändligheten får vi:
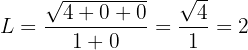
Gränsvärdet är alltså 2.
Beräkna gränsvärdet:
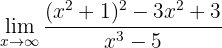
När vi betraktar funktionen mot oändligheten kan vi konstatera att:
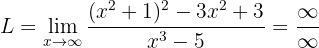
Vi måste alltså omforma funktionen för att ta bort det obestämda uttrycket.
Uppgiften kan lösas på två sätt:
1 Genom att jämföra beteendet mot oändligheten:
Först utvecklar vi kvadraten:

I täljaren har vi  och i nämnaren
och i nämnaren  som termer med högst grad. Eftersom täljarens grad är högre blir gränsvärdet
som termer med högst grad. Eftersom täljarens grad är högre blir gränsvärdet  . När graden i täljaren är högre, och termerna med högst grad har samma tecken, är gränsvärdet alltid
. När graden i täljaren är högre, och termerna med högst grad har samma tecken, är gränsvärdet alltid  .
.
2 Genom att dividera täljaren och nämnaren med termen av högsta grad:
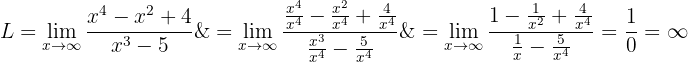
Normalt är  ett obestämt uttryck, men här får vi ett gränsvärde för
ett obestämt uttryck, men här får vi ett gränsvärde för  . Eftersom både täljaren och nämnaren växer positivt med ökande
. Eftersom både täljaren och nämnaren växer positivt med ökande  kan vi dra slutsatsen att gränsvärdet är
kan vi dra slutsatsen att gränsvärdet är  .
.
Beräkna gränsvärdet:

När vi betraktar funktionen mot oändligheten får vi:

Nämnarens oändlighet växer dock snabbare, och därför kan vi dra slutsatsen att 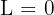 .
.
Att bevisa att gränsvärdet är 0 utan att använda L’Hôpitals regel eller regeln för högsta graden är dock mer komplicerat. Vi kan göra på följande sätt:
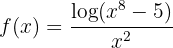
För att bestämma gränsvärdet måste vi hitta två funktioner  och
och  sådana att
sådana att 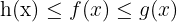 och
och

Om vi hittar sådana funktioner kan vi dra slutsatsen att
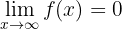 .
.
Vi kan observera att för 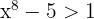 är
är 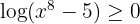 (för stora värden av
(för stora värden av  ). Dessutom är
). Dessutom är  för
för 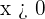 . Därför gäller:
. Därför gäller:
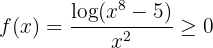
för tillräckligt stora  . Vi kan alltså välja:
. Vi kan alltså välja:
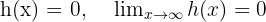
För den andra funktionen noterar vi att 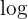 är växande, och därför är
är växande, och därför är 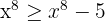 , vilket ger
, vilket ger
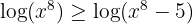
och därmed:
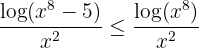
Om vi sätter 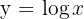 kan vi skriva:
kan vi skriva:
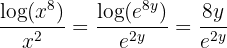
En viktig egenskap hos exponentialfunktionen är:
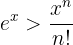
för alla  och
och 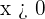 . Om vi väljer
. Om vi väljer 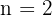 får vi:
får vi:

Därmed gäller:
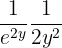
Således får vi:
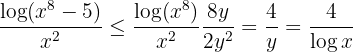
Vi kan alltså välja:
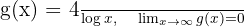
Eftersom 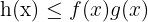 har vi därmed bevisat att:
har vi därmed bevisat att:
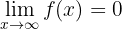
Beräkna gränsvärdet:
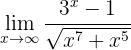
När vi betraktar funktionen mot  får vi:
får vi:
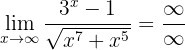
Här kan vi återigen jämföra graden av täljaren och nämnaren för att bestämma gränsvärdet. I detta fall har täljaren högre tillväxtgrad, och därför är:
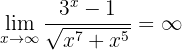
För att bevisa detta gör vi på följande sätt:

Vi behöver hitta en funktion  sådan att
sådan att 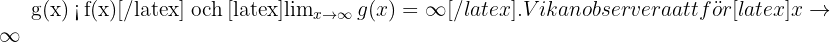 är
är  (d.v.s. radikanden är positiv för stora
(d.v.s. radikanden är positiv för stora  ). Dessutom gäller:
). Dessutom gäller:
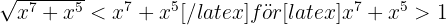 , vilket ger:
, vilket ger:
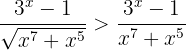
Om vi sätter  är
är 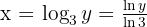 . Då gäller:
. Då gäller:
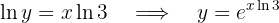
Vi får alltså 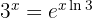 . Samtidigt vet vi att:
. Samtidigt vet vi att:
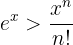 ,
,
för 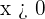 , vilket ger:
, vilket ger:
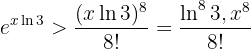
Därmed får vi:
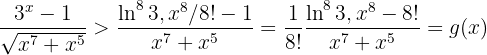
med 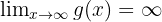 .
.
Gränsvärdet är alltså:
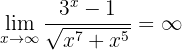
Beräkna gränsvärdet:
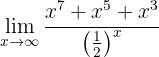
När vi betraktar funktionen mot oändligheten får vi:

Gränsvärdet måste alltså vara oändligt, eftersom både täljaren och nämnaren är positiva för stora  . För att se det tydligare kan vi skriva om uttrycket:
. För att se det tydligare kan vi skriva om uttrycket:
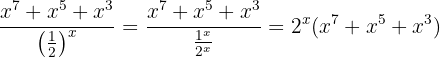
Därmed får vi:
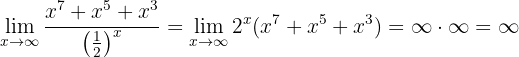
Beräkna gränsvärdet:
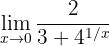
När vi betraktar funktionen mot noll får vi:

Vi får ett obestämt uttryck av formen  . I detta fall är
. I detta fall är 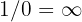 inte korrekt, eftersom vi bestämmer ett gränsvärde för
inte korrekt, eftersom vi bestämmer ett gränsvärde för 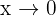 och ett positivt eller negativt
och ett positivt eller negativt  nära noll. (Vid gränsvärdesbestämning med
nära noll. (Vid gränsvärdesbestämning med  är detta vanligtvis inget problem).
är detta vanligtvis inget problem).
Därför måste vi beräkna gränsvärdena från respektive sida:
1 Först bestämmer vi vänstersidans gränsvärde:
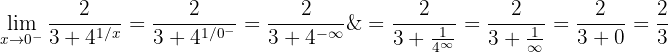
2 Nu bestämmer vi högersidans gränsvärde:
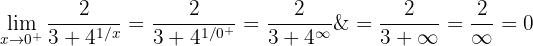
Vi ser att de två ensidiga gränsvärdena är olika, och därför finns inget gränsvärde för 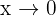 .
.
Beräkna gränsvärdet:
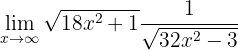
När vi betraktar funktionen mot oändligheten får vi:

Därför måste vi omforma uttrycket. Först skriver vi gränsvärdet som en enda bråkform:
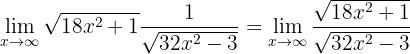
Nu delar vi täljaren och nämnaren med koefficienten för högsta graden (dvs.  , eftersom den står under en rot):
, eftersom den står under en rot):
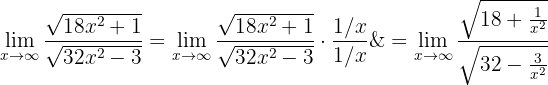
När vi nu betraktar gränsvärdet mot oändligheten får vi:
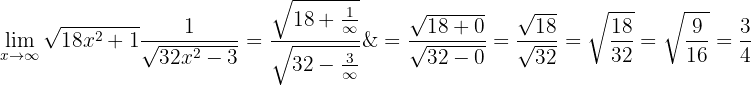
Beräkna gränsvärdet:
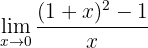
När vi betraktar funktionen mot noll får vi:
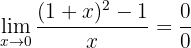
Vi har ett obestämt uttryck, därför måste vi först omforma det. Vi utvecklar kvadraten och får:
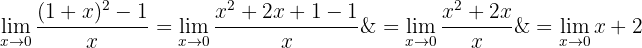
När vi nu betraktar funktionen mot noll får vi:
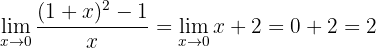
Gränsvärdet är alltså 2.
Beräkna gränsvärdet:

När vi betraktar funktionen mot 3 får vi:
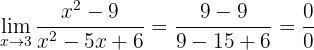
Vi får återigen ett obestämt uttryck. För att lösa det faktorisera vi både täljare och nämnare. Täljaren är en differens av kvadrater; nämnaren kan faktoriseras genom att hitta två tal som multipliceras till 6 och adderas till -5:
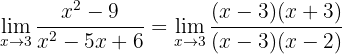
Vi kan nu ta bort  och får:
och får:
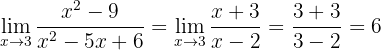
Gränsvärdet är alltså 6.
Beräkna gränsvärdet:
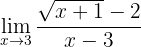
När vi betraktar funktionen mot 3 får vi:
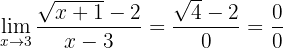
Vi får återigen ett obestämt uttryck, så vi måste omforma det först. Eftersom täljaren innehåller ett rotuttryck multiplicerar vi bråket med täljarens konjugat och delar samtidigt med det:
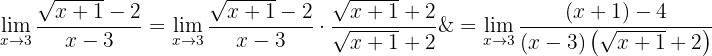
Vi förenklar sedan:
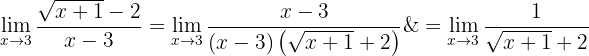
Nu kan vi ta gränsvärdet:
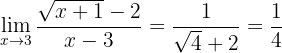
Gränsvärdet är alltså 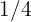 .
.
Berechne den folgenden Grenzwert:

När vi betraktar formeln mot  får vi:
får vi:

Vi får ett obestämt uttryck. Därför måste vi omforma uttrycket matematiskt för att få en form som liknar definitionen av  . Vi börjar med att lägga till och dra ifrån 2 i exponenten (gränsvärdet betecknas med
. Vi börjar med att lägga till och dra ifrån 2 i exponenten (gränsvärdet betecknas med  ):
):
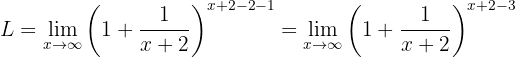
Vi omformar med potensregler:
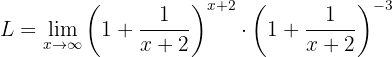
Vi ser att den första potensen motsvarar definitionen av  för
för  . Gränsvärdet blir därför:
. Gränsvärdet blir därför:
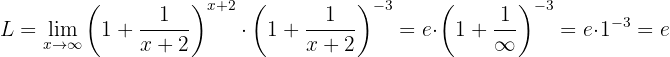
Beräkna gränsvärdet:
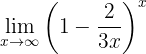
När vi betraktar uttrycket mot  får vi:
får vi:
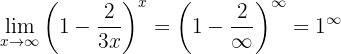
Därför måste vi omforma uttrycket matematiskt för att få en form liknande definitionen av  . Vi börjar med att skriva om uttrycket inom parentesen och betecknar gränsvärdet med
. Vi börjar med att skriva om uttrycket inom parentesen och betecknar gränsvärdet med  :
:
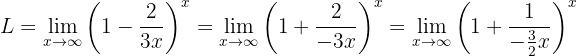
I exponenten måste vi få formen 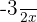 . Detta gör vi genom:
. Detta gör vi genom:
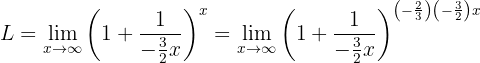
Vi omformar med potensregler:
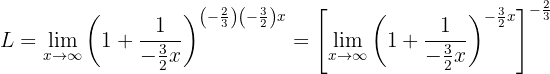
Nu kan vi beräkna gränsvärdet, eftersom vi i den yttre parentesen kan identifiera formen 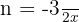 som i definitionen av
som i definitionen av  :
:
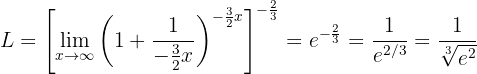
Anmärkning: formerna  ,
,  ,
, 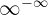 och
och 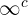 är för vissa värden av
är för vissa värden av 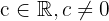 inte obestämda uttryck. Om vi får en sådan form kan vi bestämma gränsvärdet säkrare:
inte obestämda uttryck. Om vi får en sådan form kan vi bestämma gränsvärdet säkrare:
Beräkna gränsvärdet:
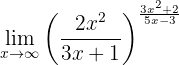
Om vi betraktar funktionen mot  ser vi omedelbart att:
ser vi omedelbart att:
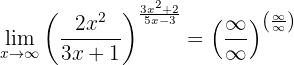
Vi jämför värdena av oändligheten i de två bråken. Först noterar vi att
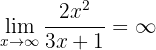 ,
,
eftersom täljaren är ett polynom av högre grad (och eftersom huvudkoefficienterna har samma tecken). På samma sätt gäller
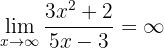 ,
,
av samma skäl. Gränsvärdet är alltså:
 ,
,
eftersom det sista uttrycket inte är ett obestämt uttryck.
Beräkna gränsvärdet:
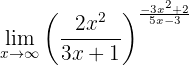
Om vi återigen betraktar funktionen mot  får vi:
får vi:
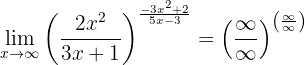
Men om vi löser gränsvärdena för bråken genom att jämföra graden av oändlighet ser vi att:
 ,
,
eftersom täljaren är ett polynom av högre grad (och huvudkoefficienterna har samma tecken). Dessutom är
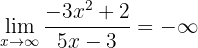 ,
,
eftersom täljaren är ett polynom av högre grad men huvudkoefficienterna inte har samma tecken. Gränsvärdet är därför:
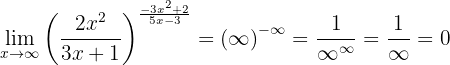
Beräkna gränsvärdet:
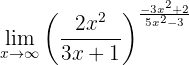
Om vi betraktar funktionen mot oändligheten får vi:

Vi betraktar gränsvärdena för bråken separat. Täljaren i basen är ett polynom av högre grad. Dessutom har huvudkoefficienterna samma tecken, därför är
 ,
,
Polynomen i exponentens täljare och nämnare har samma grad. Gränsvärdet blir alltså kvoten av huvudkoefficienterna:
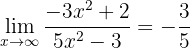
Gränsvärdet är därför
 ,
,
eftersom  när
när  .
.
Beräkna gränsvärdet:
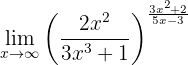
Om vi betraktar funktionen mot oändligheten får vi:
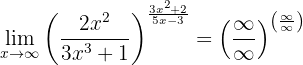
Vi betraktar gränsvärdena för bråken separat för att bestämma det generella gränsvärdet. Vi vet att
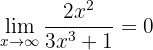 ,
,
eftersom nämnaren är ett polynom av högre grad. På samma sätt är
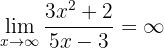 ,
,
eftersom täljaren är ett polynom av högre grad och huvudkoefficienterna har samma tecken. Gränsvärdet är alltså
 ,
,
eftersom 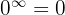 (dvs. inget obestämt uttryck).
(dvs. inget obestämt uttryck).
Beräkna gränsvärdet:
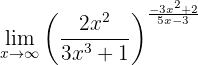
Detta gränsvärde är praktiskt taget samma som det föregående, förutom ett förändrat tecken:

Vi betraktar gränsvärdena för bråken separat för att bestämma det generella gränsvärdet. Precis som i det föregående exemplet får vi
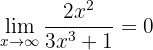 ,
,
eftersom nämnaren är ett polynom av högre grad. På samma sätt är
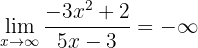 ,
,
eftersom täljaren är ett polynom av högre grad och huvudkoefficienterna har olika tecken. Gränsvärdet är alltså

Detta är ett obestämt uttryck. Vi måste därför använda regeln:

och får
Alltså är

Vi får
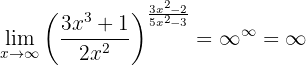
Anmärkning: det är viktigt att skriva på detta sätt.  är nämligen ett obestämt uttryck (det vill säga, vi kan konstruera olika funktioner där detta obestämda uttryck kan ge olika värden).
är nämligen ett obestämt uttryck (det vill säga, vi kan konstruera olika funktioner där detta obestämda uttryck kan ge olika värden).
Beräkna gränsvärdet:

Om vi betraktar funktionen som i det föregående exemplet mot oändligheten får vi:

Precis som tidigare betraktar vi funktionen mot oändligheten och får:
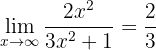 ,
,
eftersom polynomen i täljaren och nämnaren har samma grad. Gränsvärdet är alltså kvoten av huvudkoefficienterna. På samma sätt är

Det vill säga, gränsvärdet är

Beräkna gränsvärdet:

Om vi betraktar funktionen mot oändligheten får vi:
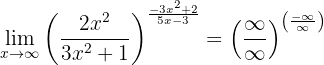
Vi betraktar gränsvärdena för bråken separat:
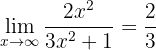 ,
,
eftersom polynomen i täljaren och nämnaren har samma grad. Gränsvärdet är alltså kvoten av huvudkoefficienterna. På samma sätt är
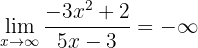 ,
,
eftersom täljaren är ett polynom av högre grad och huvudkoefficienterna har olika tecken. Gränsvärdet är alltså
 ,
,
eftersom vi får ett uttryck av formen 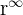 med
med 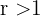 .
.
Beräkna gränsvärdet:
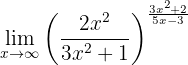
Om vi betraktar funktionen mot oändligheten får vi:
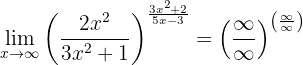
Detta gränsvärde är praktiskt taget detsamma som det föregående, förutom ett ändrat tecken. Vi betraktar gränsvärdena för bråken separat:
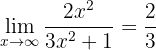 ,
,
eftersom polynomen i täljaren och nämnaren har samma grad. Gränsvärdet är alltså kvoten av huvudkoefficienterna. På samma sätt är
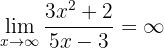 ,
,
eftersom täljaren är ett polynom av högre grad och huvudkoefficienterna har samma tecken. Gränsvärdet är alltså
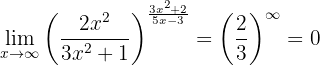 ,
,
eftersom vi får ett uttryck av formen 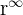 med
med 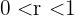 .
.
Sammanfatta med AI:












