Att beräkna kvadratroten av ett tal kan verka skrämmande om man inte har rätt verktyg. Som tur är finns det olika metoder som kan hjälpa dig att beräkna kvadratroten för att få exakta resultat. I den här artikeln får du lära dig hur du kan beräkna kvadratroten med olika metoder, så att du kan välja den som passar dig bäst.

Steg för att beräkna kvadratroten
För att lösa en kvadratrot följer vi stegen i följande exempel:
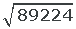
1 Om radikanden består av fler än två siffror delas siffrorna upp i par, med start från höger.

2 Vi beräknar den heltaliga eller exakta kvadratroten av den första siffergruppen från vänster, i det här fallet (8)

Vi frågar oss: Vilket tal i kvadrat blir 8?
Vi ser att 8 inte är ett perfekt kvadrattal, utan ligger mellan två perfekta kvadrater: 4 och 9
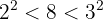
Vi tar kvadratroten av den perfekta kvadraten som är mindre än 8, dvs. kvadratroten ur 4, vilket är 2, och sätter det i motsvarande ruta.
3 Kvadraten av den erhållna roten 2 (dvs. 4) subtraheras från den första siffergruppen i radikanden (8).
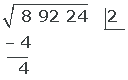
Med andra ord: Kvadraten av 2 är 4. Vi subtraherar 4 från 8 och får 4.
4 Vi skriver den andra siffergruppen av radikanden under strecket, separerar den första siffran från höger (2) från den bildade siffran (492) och dividerar resten med det dubbla av roten 2, alltså 2·2 = 4.
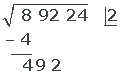
Med andra ord:
- Vi tar ner 92 och får talet 492 att arbeta med.
- Vi separerar första siffran från höger (2) och det blir 49 kvar.
- Vi dividerar 49 med det dubbla av den tidigare roten, 4.
Eftersom resultatet av 49 ÷ 4 är större än 9, tar vi 9 som kvot.
Anmärkning: Vi tar 9 om resultatet av divisionen (49 ÷ 4) är större än 9.
5 I nästa rad under roten skriver vi det dubbla av roten (4) samt den erhållna kvoten (9). Därefter multiplicerar vi det erhållna talet (49) med kvoten (9). Sedan subtraherar vi 441 från radikandens tal 492.
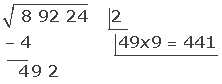
- Vi skriver nästa rad med det dubbla av roten, vilket i det här fallet är 4.
- Vi skriver den erhållna kvoten (9) efter 4 och får talet 49.
- Vi multiplicerar 49 med 9 och får 441.
- Vi subtraherar 441 från 492.
Hinweis: Wenn wir einen Wert erhalten hätten, der größer als die berechenbare Menge des Radikanden ist, hätten wir es mit 8, mit 7... versucht, bis wir einen niedrigeren Wert gefunden hätten.
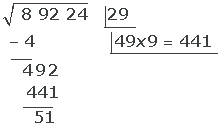
Anmärkning: Om vi fått ett värde som är större än det beräkningsbara talet från radikanden, hade vi försökt med 8, sedan 7… tills vi hittar ett mindre värde.
6 Den erhållna kvoten (9) blir den andra siffran under roten; resten är 29.
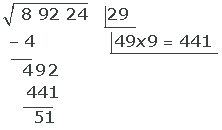
7 Vi tar ner nästa sifferpar och upprepar föregående steg.
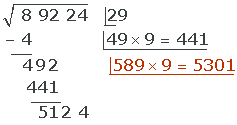
Eftersom 5301 > 5124, provar vi med talet 8.
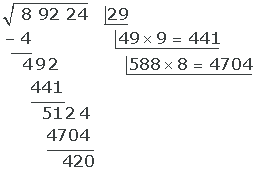
Således:
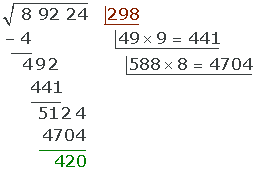
Och på detta sätt avslutar vi beräkningen.
8 Kontroll av kvadratroten. För att resultatet ska vara korrekt måste följande villkor uppfyllas:
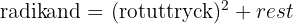
De erhållna värdena uppfyller villkoret.
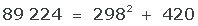
Exempel med kvadratrötter
Beräkna kvadratrötterna av:
1 Beräkning
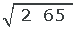
Vi tillämpar de tidigare stegen och får:
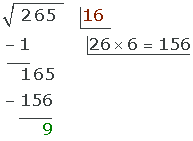
Vi avslutar beräkningen.
2 Beräkning
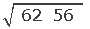
Vi beräknar:
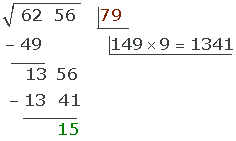
3 Beräkning

Vi beräknar:
Sammanfatta med AI:












