Kapitel

Lös följande integraler
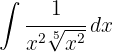
För att lösa integralen för vi upp nämnaren och förenklar potenserna. Slutligen tillämpar vi potensregeln.
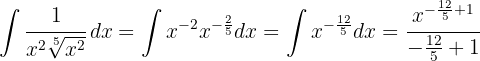
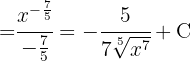
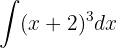
För att lösa integralen substituerar vi  och tillämpar potensregeln.
och tillämpar potensregeln.


För att lösa integralen substituerar vi 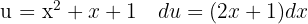 och tillämpar potensregeln.
och tillämpar potensregeln. 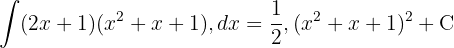

För att lösa integralen substituerar vi 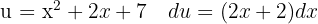 och tillämpar potensregeln.
och tillämpar potensregeln.

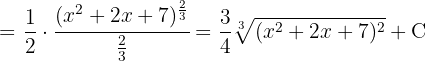
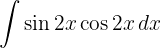
För att lösa integralen substituerar vi  och tillämpar potensregeln.
och tillämpar potensregeln.
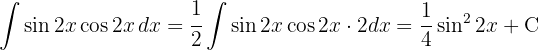
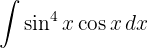
För att lösa integralen substituerar vi  och tillämpar potensregeln.
och tillämpar potensregeln.
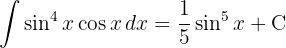
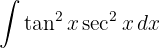
För att lösa integralen substituerar vi 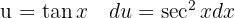 och tillämpar potensregeln.
och tillämpar potensregeln.
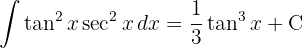
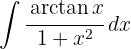
För att lösa integralen substituerar vi  och tillämpar potensregeln.
och tillämpar potensregeln.
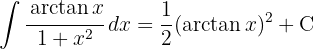
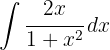
För att lösa integralen substituerar vi  och integrerar
och integrerar  .
.
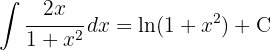
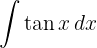
För att lösa integralen skriver vi om tangensfunktionen i form av sinus och cosinus och integrerar slutligen  .
.


För att lösa integralen substituerar vi 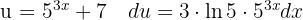 och integrerar
och integrerar  .
.

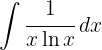
För att lösa integralen substituerar vi 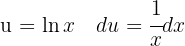 och integrerar
och integrerar  .
.
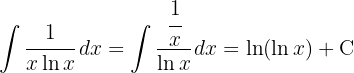

För att lösa integralen substituerar vi  och integrerar
och integrerar  .
.

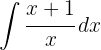
För att lösa integralen separerar vi integralen och integrerar slutligen  .
.
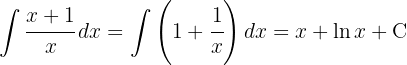
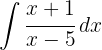
För att lösa integralen lägger vi till en nolla så att vi kan dela upp den i två integraler och integrerar slutligen  .
.


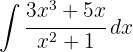
För att lösa integralen börjar vi först med en förenklad polynomdivision så att vi kan dela upp den i två integraler. Och slutligen integrerar vi  med en substitution
med en substitution  .
.
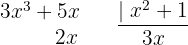
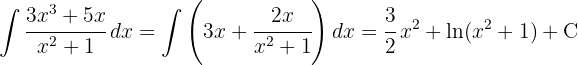
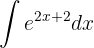
För att lösa integralen substituerar vi  och integrerar slutligen
och integrerar slutligen  .
.
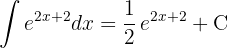

För att lösa integralen integrerar vi 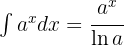 .
.

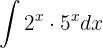
För att lösa integralen integrerar vi 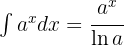 .
.
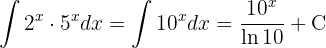
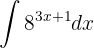
För att lösa integralen substituerar vi 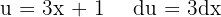 och integrerar slutligen
och integrerar slutligen 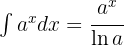 .
.
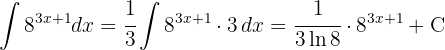
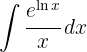
För att lösa integralen substituerar vi 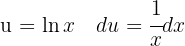 och integrerar slutligen
och integrerar slutligen  .
.
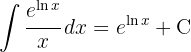 .
.

För att lösa integralen substituerar vi  och integrerar slutligen
och integrerar slutligen  .
.


För att lösa integralen substituerar vi 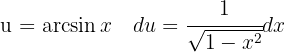 och integrerar slutligen
och integrerar slutligen  .
.
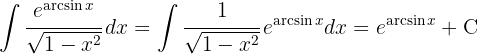
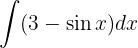
Vi börjar med att dela upp integralen och integrerar var för sig 


Vi börjar med att substituera 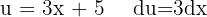 och integrerar slutligen
och integrerar slutligen 
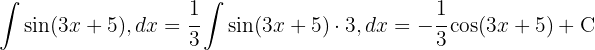

Vi börjar med att substituera 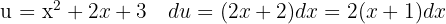 och integrerar slutligen
och integrerar slutligen 
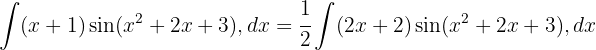
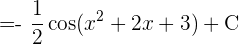
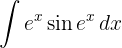
Vi börjar med att substituera 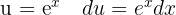 och integrerar slutligen
och integrerar slutligen 
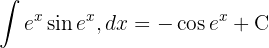

Vi börjar med att substituera  och integrerar slutligen
och integrerar slutligen 
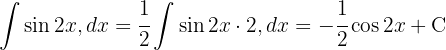

Vi börjar med att tillämpa 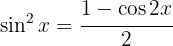 , delar upp integralen och integrerar slutligen
, delar upp integralen och integrerar slutligen  . Vi substituerar
. Vi substituerar  .
.
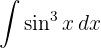
Vi börjar med att dela upp sinus och tillämpar den trigonometriska funktionen 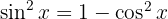 . Slutligen integrerar vi
. Slutligen integrerar vi  och substituerar
och substituerar 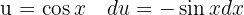
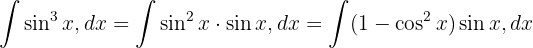
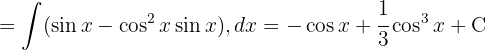
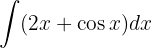
Vi delar upp integralen och integrerar slutligen 

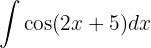
Vi börjar med att substituera 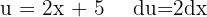 och integrerar slutligen
och integrerar slutligen 
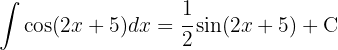
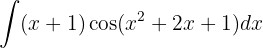
Vi börjar med att substituera 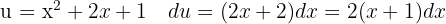 och integrerar slutligen
och integrerar slutligen 
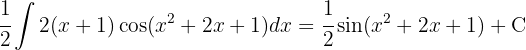

Vi börjar med att substituera  och integrerar slutligen
och integrerar slutligen 
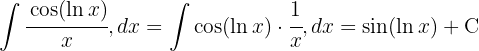

Vi tillämpar den trigonometriska funktionen 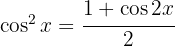 , delar upp integralen och integrerar slutligen
, delar upp integralen och integrerar slutligen  . Vi substituerar
. Vi substituerar 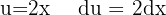
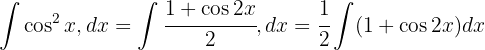
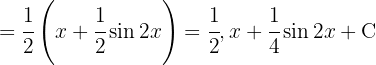

Vi tillämpar den trigonometriska funktionen 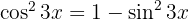 , delar upp integralen och integrerar
, delar upp integralen och integrerar  . Vi substituerar
. Vi substituerar 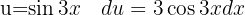
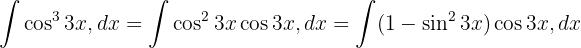
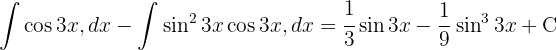
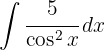
Vi tillämpar den trigonometriska funktionen 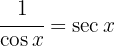 och integrerar slutligen
och integrerar slutligen 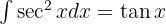
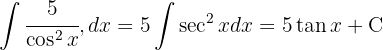
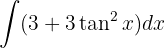
Vi tillämpar den trigonometriska funktionen  och integrerar slutligen
och integrerar slutligen 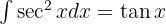
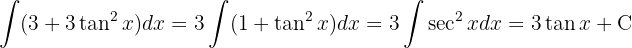

Vi börjar med att substituera  och integrerar slutligen
och integrerar slutligen 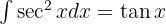
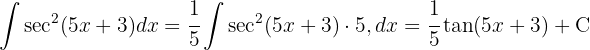

Vi delar upp sekans och tillämpar den trigonometriska funktionen  , integrerar
, integrerar 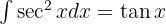 och substituerar
och substituerar 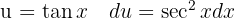
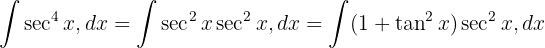

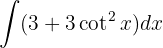
För att lösa integralen tillämpar vi den trigonometriska funktionen 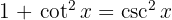 och integrerar slutligen
och integrerar slutligen 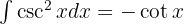
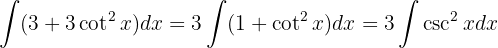
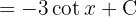

Vi börjar med att lägga till en nolla, tillämpar den trigonometriska funktionen  , delar upp integralen och integrerar slutligen
, delar upp integralen och integrerar slutligen 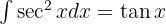
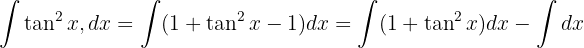
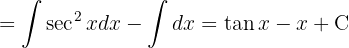
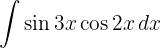
För att lösa integralen bestämmer vi värdena för A och B som uppfyller följande ekvation


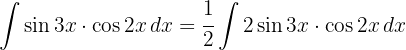
Vi substituerar 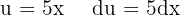 och integrerar slutligen
och integrerar slutligen 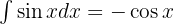
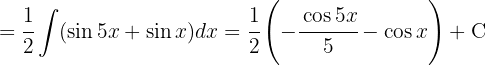
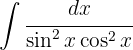
För att lösa integralen tillämpar vi den trigonometriska funktionen  , delar upp integralen och förenklar
, delar upp integralen och förenklar


Nu tillämpar vi 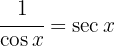 och
och 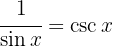 och integrerar slutligen
och integrerar slutligen  och
och 
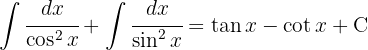
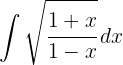
För att lösa följande integral multiplicerar vi täljare och nämnare med  och delar upp integralen
och delar upp integralen
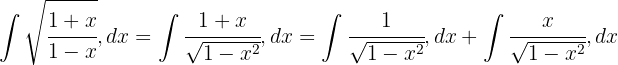
Vi integrerar  och substituerar
och substituerar 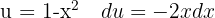



För att lösa följande integral multiplicerar vi täljare och nämnare med 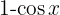 , beräknar binomet i kvadrat, tillämpar
, beräknar binomet i kvadrat, tillämpar 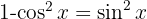 och delar upp integralen
och delar upp integralen
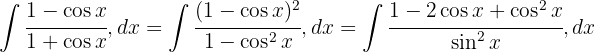
Nu tillämpar vi 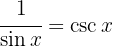 , integrerar
, integrerar  , substituerar
, substituerar  och lägger till en nolla för att kunna tillämpa
och lägger till en nolla för att kunna tillämpa 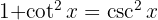 och slutligen integralen
och slutligen integralen 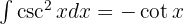
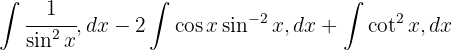
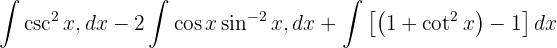
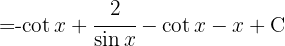

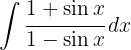
För att lösa följande integral multiplicerar vi täljare och nämnare med 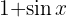 , beräknar binomet i kvadrat, tillämpar
, beräknar binomet i kvadrat, tillämpar 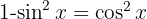 och delar upp integralen
och delar upp integralen
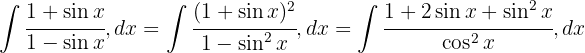
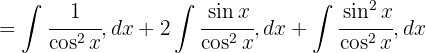
Nu tillämpar vi 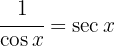 , integrerar
, integrerar 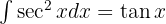 , substituerar
, substituerar 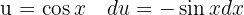 och lägger till en nolla för att kunna tillämpa
och lägger till en nolla för att kunna tillämpa 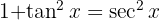
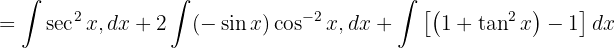
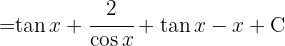
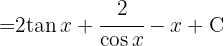

För att lösa följande integral måste vi komplettera så att vi får en integral av formen 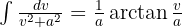 , där
, där 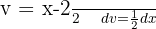 .
.
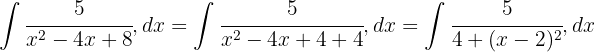
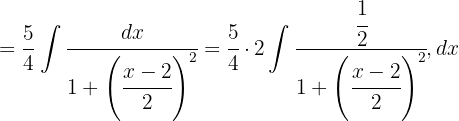
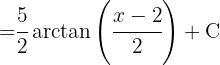

Vi delar upp integralen och substituerar på ena sidan  . På andra sidan vill vi få en integral av formen
. På andra sidan vill vi få en integral av formen 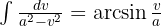 , där
, där 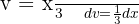 .
.
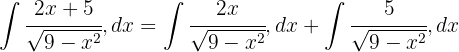
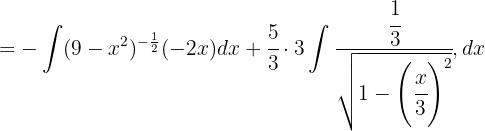


Vi vill få en integral av formen 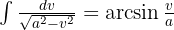 , där
, där 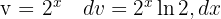 .
.

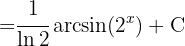
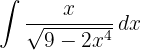
Vi vill få en integral av formen 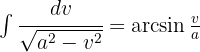 och går tillväga enligt följande i nämnaren:
och går tillväga enligt följande i nämnaren:
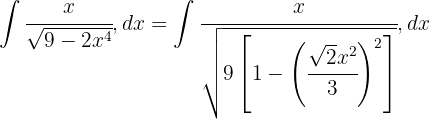
där 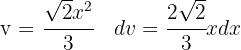 .
.
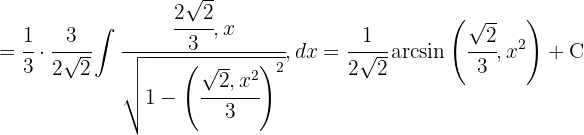
Sammanfatta med AI:











