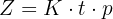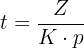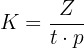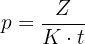Vad är ränta och hur beräknas den?
Vanligtvis tas en månatlig ränta ut av banker, sparkonton, lån och pantbrev. Det finns dock olika typer av räntesatser.
En räntesats kan tas ut årligen, månadsvis eller till och med dagligen, beroende på löptiden. Man talar då om års-, månads- eller dagsränta.
I de följande räkneexemplen utgår vi från årsbaserad ränta.
Vidare skiljer man mellan enkel ränta och ränta på ränta. I våra uppgifter räknar vi endast med enkel ränta.
Ränteformler
Följande förkortningar används i räkneexemplen:
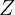: Räntebelopp
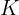: Startkapital
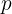: Räntesats
: Löptid
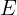: Slutkapital
Formler för enkel ränta, när räntesats och löptid anges i samma tidsenhet:
Observera: Om löptid och räntesats anges i olika enheter måste formlerna först omvandlas till samma tidsenhet.
Blandade räkneuppgifter
För vilken löptid måste ett kapital placeras till 5 % ränta för att få ett slutkapital på 30 000 €?
Kända är startkapital och slutkapital. Följaktligen måste först skillnaden däremellan, dvs. ränteökningen i €, beräknas:
€
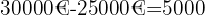Med hjälp av ränteökningen beräknar vi löptiden:
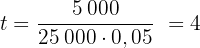
Kapitalet måste alltså placeras i 4 år:
En bank ger ett lån på 45 000 € och får efter 1 år, 4 månader och 15 dagar ett slutkapital på 52 500 €.
Beräkna räntesatsen (i procent).
Beräkna löptiden i dagar
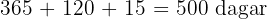
Beräkna räntan
52 500 € - 45 000 € = 7 500 €
Beräkna räntesatsen (%)
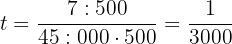
Tänk på att detta är räntesatsen för dagsränta. För att få års ränta, multiplicera först med 365. Multiplicera sedan resultatet med 100 för att få procent:
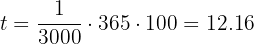
Årsräntan är alltså 12,16 %.
Bestäm den enkla räntesatsen (i %), med vilken ett lån måste tas, för att efter en löptid på 20 år ha betalat lika mycket ränta som lånebeloppet.
Räntebeloppet ska motsvara storleken på det upplånade lånet.
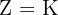
Ersätt räntebeloppet 
i formeln med 
:
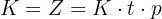
Eftersom kapitalet (dvs. lånebeloppet) är skilt från noll, kan på båda sidor av ekvationen elimineras:
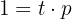
Lös för räntesatsen:
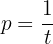
Löptiden är 20 år, det vill säga:
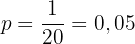
Räntesatsen är alltså 0,05. I procentform (multiplicerat med 100) blir det 5 %.
Efter hur lång tid blir räntan tre gånger så stor som startkapitalet, som placerats till en ränta på 6 %?
Räntan måste vara tre gånger så stor som startkapitalet, det vill säga:
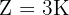
Sätt in värdet i ränteformeln för beräkning av :
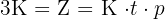
Eliminera och lös för 
:
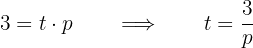
Sätt in räntesatsen, och tänk på att räntesatsen 6 % skrivs som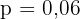 
:
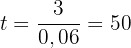
Löptiden är alltså 50 år.
Bestäm vilket totalt räntebelopp man får om ett kapital på 30 000 € placeras till enkel ränta på 6 %.
Här ska räntebeloppet beräknas. Sätt in den kända informationen i den allmänna ränteformeln:
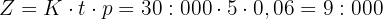
Efter 5 år blir det totala räntebeloppet alltså 9 000 €.
Beräkna slutkapitalet vid placering av ett startkapital på 10 000 € med en ränta på 3,5 % efter 6 månader.
För att lösa uppgiften måste räntebeloppet för 6 månader beräknas. Eftersom det är en årsbaserad ränta, omvandlas först 6 månader till år, det vill säga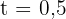 
.
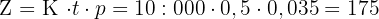
Med hjälp av räntebeloppet kan slutkapitalet nu beräknas med följande formel:
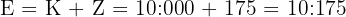
Slutkapitalet efter en löptid på 6 månader blir alltså 10 175 €.
Gillade du den här artikeln? Betysätt den!
Loading...