Optimering av produktionen i en lampfabrik
Ett företag tillverkar två typer av lampor, modell L1 och modell L2, och säljer dessa.
För att producera modell L1 krävs 20 minuter manuellt arbete och för modell L2 krävs 30 minuter manuellt arbete. Modell L1 kräver dessutom 20 minuter maskinarbete, medan modell L2 kräver 10 minuter maskinarbete.
Företaget har tillgång till totalt 100 timmar manuellt arbete och 80 timmar maskinarbete per månad. Vinsten per såld lampa är 15 € för modell L1 och 10 € för modell L2.
Under vilka förutsättningar uppnås den högsta vinsten?
Ett företag tillverkar två typer av lampor, modell L1 och L2, och säljer dessa.
För att producera modell L1 krävs 20 minuter manuellt arbete, och för modell L2 krävs 30 minuter manuellt arbete. Modell L1 kräver dessutom 20 minuter maskinarbete, medan modell L2 kräver 10 minuter maskinarbete.
Företaget har tillgång till totalt 100 timmar manuellt arbete och 80 timmar maskinarbete per månad. Vinsten per såld lampa är 15 € för modell L1 och 10 € för modell L2.
Frågan är: Under vilka förutsättningar uppnås den högsta vinsten?
1 Definiera de obekanta
x = antal lampor av modell L1
y = antal lampor av modell L2
2 Målfunktion
f(x, y) = 15x + 10y
3 Bivillkor (restriktioner)
Omvandla tidsangivelserna till timmar:
- 20 min = 1/3 h
- 30 min = 1/2 h
- 10 min = 1/6 h
För att definiera restriktionerna presenterar man alla värden i en tabell:
| L1 | L2 | Tillgänglig tid (h) | |
|---|---|---|---|
| Manuellt arbete | 1/3 | 1/2 | 100 |
| Maskinarbete | 1/3 | 1/6 | 80 |
- 1/3x + 1/2y ≤ 100
- 1/3x + 1/6y ≤ 80
Eftersom antalet lampor inte kan vara negativt gäller dessutom:
- x ≥ 0
- y ≥ 0
4 Mängden av möjliga lösningar
För att bestämma den möjliga lösningsmängden ritar man upp bivillkoren grafiskt.
Eftersom x ≥ 0 och y ≥ 0 behöver vi bara betrakta första kvadranten.
Rita linjerna i koordinatsystemet och markera skärningspunkterna med respektive axel.
Lös olikheten med den grafiska metoden:
1/3 x + 1/2 y ≤ 100;
Välj en punkt i planet, till exempel (0,0).
1/3·0 + 1/2·0 ≤ 100
1/3·0 + 1/6·0 ≤ 80
Det område där lösningarna till olikheterna överlappar utgör den tillåtna lösningsmängden.
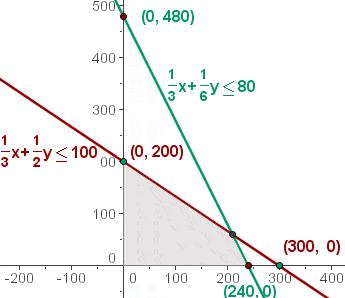
5 Bestäm nu vilka koordinater hörnpunkterna i den tillåtna (feasibla) lösningsmängden har.
Om det finns bara en optimal lösning ligger den i ett hörn. Här är lösningarna till systemet:
1/3x + 1/2y = 100; x = 0 (0, 200)
1/3x + 1/6y = 80; y = 0(240, 0)
1/3x + 1/2y = 100; 1/3x + 1/6y = 80(210, 60)
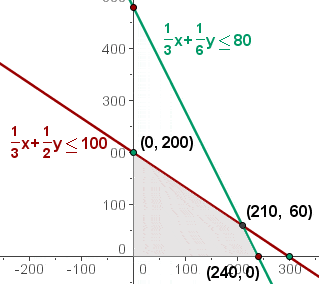
6 Beräkna nu värdet på målfunktionen
Sätt in värdena för varje hörn i målfunktionen.
f(x, y) = 15x + 10y
f(0, 200) = 15·0 + 10·200 = 2 000 €
f(240, 0 ) = 15·240 + 10·0 = 3 600 €
f(210, 60) = 15·210 + 10·60 = 3 750 € (Maximalt värde)
Den optimala lösningen är att tillverka 210 lampor av modell L1 och 60 lampor av modell L2 för att uppnå en vinst på 3 750 €.
Optimering vid försäljning av skolmaterial
I början av det nya skolåret finns skolmaterial till försäljning.
Ett varuhus vill erbjuda 600 skrivhäften, 500 mappar och 400 kulspetspennor i form av två olika paket:
- Paket 1 innehåller 2 skrivhäften, 1 mapp och 2 kulspetspennor.
- Paket 2 innehåller 3 skrivhäften, 1 mapp och 1 kulspetspenna.
- Försäljningspriset är 6,50 € för paket 1 och 7 € för paket 2.
Frågan är: Hur många paket av varje typ bör tillverkas för att uppnå högsta möjliga vinst?
I början av det nya skolåret finns skolmaterial till försäljning.
Ett varuhus vill erbjuda 600 skrivhäften, 500 mappar och 400 kulspetspennor i form av två olika paket:
- Paket 1 innehåller 2 skrivhäften, 1 mapp och 2 kulspetspennor.
- Paket 2 innehåller 3 skrivhäften, 1 mapp och 1 kulspetspenna.
- Försäljningspriset är 6,50 € för paket 1 och 7 € för paket 2.
Frågan är: Hur många paket av varje typ bör tillverkas för att uppnå högsta möjliga vinst?
1 Definiera de obekanta
x = P1
y = P2
2 Målfunktion
f(x, y) = 6.5x + 7y
3 Restriktioner
| Material | P1 | P2 | Tillgång |
|---|---|---|---|
| Skrivhäften | 2 | 3 | 600 |
| Mappar | 1 | 1 | 500 |
| Kulspetspennor | 2 | 1 | 400 |
Matematiska uttryck:
- 2x + 3y ≤ 600
- x + y ≤ 500
- 2x + y ≤ 400
- x ≥ 0
- y ≥ 0
4 Bestäm mängden av möjliga lösningar
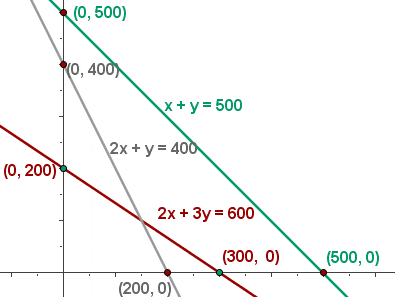
5 Bestäm vilka koordinater hörnpunkterna i den tillåtna lösningsmängden har.
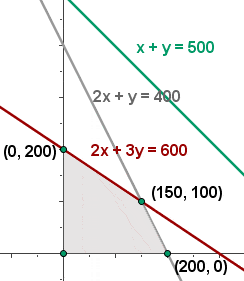
6 Beräkna värdet på målfunktionen
f(x,y) = 6.5 · 200 + 7 · 0 = 1300 €
f(x,y)= 6.5 · 0 + 7 · 200 = 1 400 €
f(x,y)= 6.5 · 150 + 7 · 100 = 1 675 € , dvs. man fa˚r ett maximalt va¨rde.
Den optimala lösningen är att sälja 150 paket av P1 och 100 paket av P2 för att uppnå en vinst på 1 675 €.
Optimering av utfodringen på en gård
På en hönsgård ges djuren foder för snabb viktökning, som ska innehålla minst 15 enheter av näringsämne A och 15 enheter av näringsämne B.
På marknaden erbjuds två typer av foder:
- Foder X innehåller 1 enhet av näringsämne A och 5 enheter av näringsämne B.
- Foder Y innehåller 5 enheter av näringsämne A och 1 enhet av näringsämne B.
- Priset är 10 € för foder X och 30 € för foder Y.
Frågan är: Hur mycket av varje foder bör köpas för att täcka behovet till lägsta möjliga kostnad?
1 Definiera de obekanta
x = X
y = Y
2 Målfunktion
f(x,y) = 10x + 30y
3 Restriktioner
| Ingrediens | X | Y | Minst |
|---|---|---|---|
| A | 1 | 5 | 15 |
| B | 5 | 1 | 15 |
Matematiska uttryck:
- x + 5y ≥ 15
- 5x + y ≥ 15
- x ≥ 0
- y ≥ 0
4 Bestäm mängden av möjliga lösningar
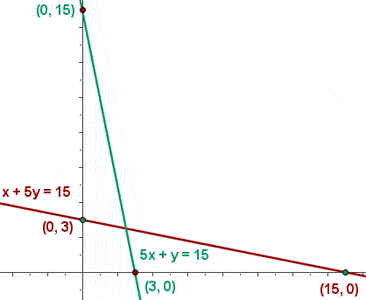
5 Bestäm vilka koordinater hörnpunkterna i den tillåtna lösningsmängden har.
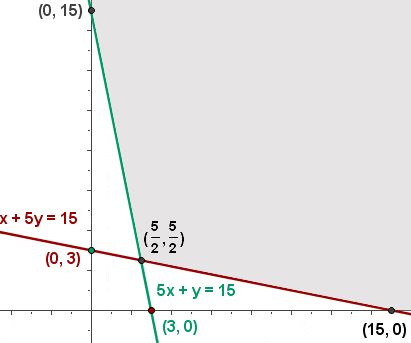
6 Beräkna värdet på målfunktionen
f(0, 15) = 10 · 0 + 30 · 15 = 450
f(15, 0) = 10 · 15 + 30 · 0 = 150
f(5/2, 5/2) = 10 · 5/2 + 30 · 5/2 = 100 (minst)
De lägsta kostnaderna är 100 € för X = 5/2 och Y = 5/2.
Optimering vid tillverkning av läkemedel
En läkemedelstillverkare har 600 g av ett läkemedel för att producera stora och små tabletter.
- De stora tabletterna ska väga 40 g vardera.
- De små tabletterna ska väga 30 g vardera.
- För en förpackning stora tabletter krävs minst tre tabletter, och för en förpackning små tabletter minst dubbelt så många.
Varje tablett ger en vinst på 2 € (stora tabletter) respektive 1 € (små tabletter).
Frågan är: Hur många tabletter av varje typ bör tillverkas för att uppnå maximal vinst?
1 Definiera de obekanta
- x = antal stora tabletter
- y = antal små tabletter
2 Målfunktion
f(x, y) = 2x + y
3 Restriktioner
- 40x + 30y ≤ 600
- x ≥ 3
- y ≥ 2x
- x ≥ 0
- y ≥ 0
4 Bestäm mängden av möjliga lösningar
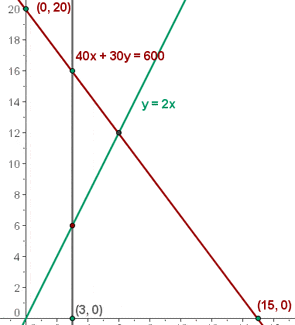
5 Bestäm vilka koordinater hörnpunkterna i den tillåtna lösningsmängden har.
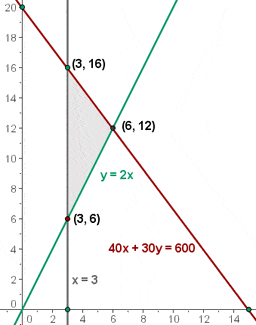
6 Beräkna värdet på målfunktionen
f(x, y) = 2 · 3 + 16 = 22 €
f(x, y) = 2 · 3 + 6 = 12 €
f(x, y) = 2 · 6 + 12 = 24 € (Maximalt)
Den högsta vinsten på 24 € uppnås när 6 stora tabletter och 12 små tabletter tillverkas.
Optimering vid utförsäljning i klädbutik
Ett varuhus vill erbjuda 200 skjortor och 100 byxor från föregående säsong till specialpriser.
Två erbjudanden ska tas fram:
- Erbjudande A innehåller ett set med en skjorta och ett par byxor, som ska säljas för 30 €.
- Erbjudande B innehåller ett set med tre skjortor och ett par byxor, som ska säljas för 50 €.
- Minst 20 set av erbjudande A och 10 set av erbjudande B ska förberedas.
Frågan är: Hur många set av varje typ bör säljas för att uppnå maximal vinst?
1 Definiera de obekanta
- x = antal set av erbjudande A
- y = antal set av erbjudande B
2 Målfunktion
f(x, y) = 30x + 50y
3 Restriktioner
| Material | A | B | Minst |
|---|---|---|---|
| Skjortor | 1 | 3 | 200 |
| Byxor | 1 | 1 | 100 |
Matematiska uttryck:
- x + 3y ≤ 200
- x + y ≤ 100
- x ≥ 20
- y ≥ 10
4 Bestäm mängden av möjliga lösningar
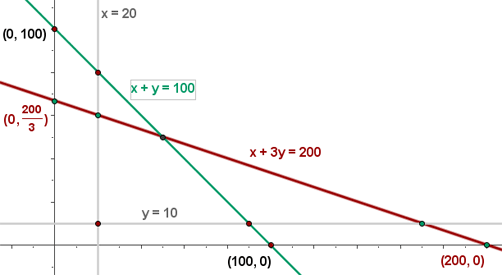
5 Bestäm vilka koordinater hörnpunkterna i den tillåtna lösningsmängden har.
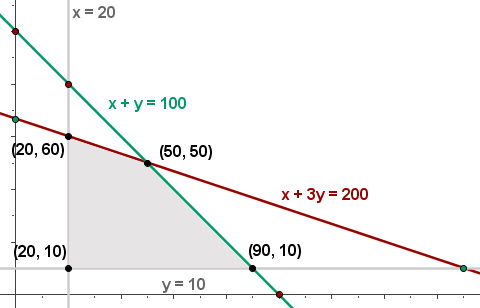
6 Beräkna värdet på målfunktionen
f(x, y) = 30 · 20 + 50 · 10 = 1100 €
f(x, y) = 30 · 90 + 50 · 10 = 3200 €
f(x, y) = 30 · 20 + 50 · 60 = 3600 €
f(x, y) = 30 · 50 + 50 · 50 = 4000 € (maximalt)
Den maximala vinsten på 4 000 € uppnås när man säljer 50 set av vardera erbjudande.
Sammanfatta med AI:


