Övningsuppgifter för linjära ekvationer

Eliminera den obekanta genom att dividera båda sidor med . Du kan också säga att :an, som multiplicerades i den första termen, divideras i den andra termen.

När du samlar ihop likadana termer måste du addera de båda termerna och för att få en ekvivalent ekvation.

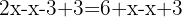
I praktiken sägs det ofta att en term som adderas med i en led övergår till den andra leden genom subtraktion av , och när finns kvar övergår den till den andra leden genom addition av . Addera:

Använd distributiviteten för att lösa upp parentesen, det vill säga du multiplicerar varje algebraisk term som finns inom parentesen med så att på vänster sida står följande:

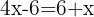
Gruppera likadana termer, det adderade x:et flyttas över till andra sidan genom subtraktion och den kvarvarande :an adderas. Addera alltså:

Eliminera den obekanta, :an flyttas över till andra sidan genom division

För att ta bort nämnarna måste du hitta den minsta gemensamma multipeln av och

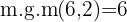
Multiplicera båda delarna av ekvationen med detta värde, i detta fall , och du får:

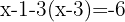
Multiplicera med hjälp av distributiviteten, lös upp parentesen, gruppera och addera likadana termer:

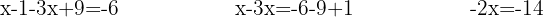
Lös ut den obekanta:

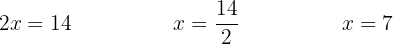
Multiplicera med varje term inom parentesen (distributiva egenskapen), för att lösa upp parentesen och förenkla:

Gruppera och addera likadana termer:

Med hjälp av distributiviteten för att lösa upp parenteserna multiplicerar man den första parentesen med och den andra med .

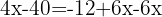
Samla ihop likadana termer

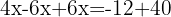
Addera de likadana termerna och lös för x

Lös upp parentesen med hjälp av distributiviteten genom att multiplicera den första parentesen med och den andra parentesen med .

Samla ihop likadana termer

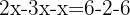
Addera de likadana termerna och lös för x

För att eliminera nämnarna måste du hitta den minsta gemensamma multipeln av , och

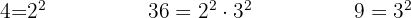
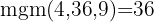
Dividera den gemensamma nämnaren med varje nämnare och multiplicera resultatet med motsvarande täljare

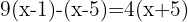
Multiplicera ut parenteserna med hjälp av distributiva lagen: den första med , den andra med

och den tredje med .

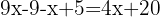
Gruppera lika termer tillsammans

Addera de lika termerna och lös ut x

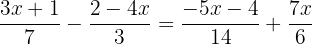
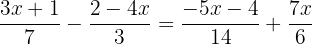
För att eliminera nämnarna måste du hitta den minsta gemensamma multipeln av , , och .

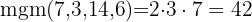
Dividera den gemensamma nämnaren med varje nämnare och multiplicera resultatet med motsvarande täljare:

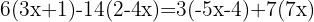
Multiplicera ut parenteserna med hjälp av distributiva lagen:

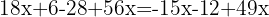
Samla lika termer:

Förenkla:

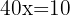
Lös ut x:

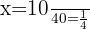
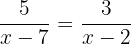
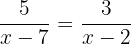För att likheten mellan de två bråken ska vara uppfylld måste produkten av ytterlemmarna vara lika med produkten av mellanlemmarna (korsmultiplikation).

Som alternativ kan du också hitta den minsta gemensamma multipeln, som är

eftersom de två binomen inte kan förkortas. Då dividerar du den gemensamma nämnaren med varje nämnare och resultatet multipliceras med motsvarande täljare.

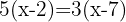
Multiplicera ut parenteserna med hjälp av distributiva lagen: den första parentesen med och den andra med .

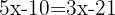
Samla lika termer:

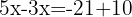
Lös ut den obekanta:

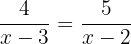
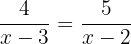
För att likheten mellan de två bråken ska vara uppfylld måste produkten av ytterlemmarna vara lika med produkten av mellanlemmarna (korsmultiplikation).

Som alternativ kan du också hitta den minsta gemensamma multipeln, som är 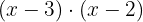, eftersom de två binomen inte kan förkortas. Då dividerar du den gemensamma nämnaren med varje nämnare och resultatet multipliceras med motsvarande täljare.

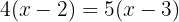
Multiplicera ut parenteserna med hjälp av distributiva lagen: den första parentesen med och den andra med .

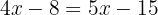
Samla lika termer:

Lös ut den obekanta:

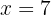
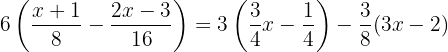
Här är den svenska översättningen:

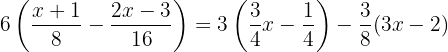
Multiplicera ut parenteserna med hjälp av distributiva lagen: den första parentesen med , den andra med och den tredje med .

Bra att veta: När ett heltal multipliceras med ett bråk löser du detta genom att multiplicera heltalet med täljaren i bråket medan nämnaren förblir densamma.

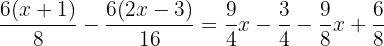
Använd distributiva lagen för att lösa upp parenteserna i täljarna:

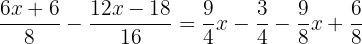
För att eliminera nämnarna måste du hitta den minsta gemensamma multipeln av , och .

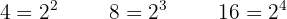
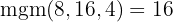
Dividera den gemensamma nämnaren med varje nämnare och multiplicera resultatet med motsvarande täljare:

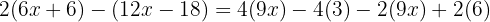
Använd distributiva lagen för att lösa upp parenteserna: multiplicera den första parentesen med och förenkla med hänsyn till teckenväxling:

Samla lika termer:

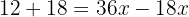
Lös ut den obekanta:

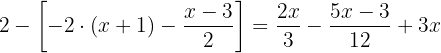
Här är den svenska översättningen:

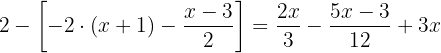
I detta fall är det lämpligt att först lösa upp termen 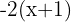. När du löser upp kan du ersätta den hakparentesen med en vanlig parentes.

Multiplicera termerna inom parentesen med -1, så att du kan ta bort det negativa tecknet och parentesen från ekvationen:

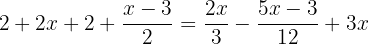
För att eliminera nämnarna måste du hitta den minsta gemensamma multipeln av 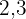och .

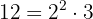
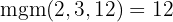
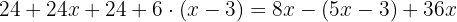
Multiplicera ut parenteserna med hjälp av distributiva lagen: den första parentesen med och den andra med :

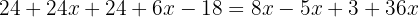
Samla lika termer:

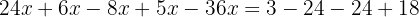
Addera:

Dividera båda leden med :

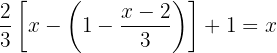
Här är den svenska översättningen:

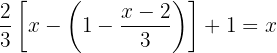
Multiplicera termerna inom parentesen med , så att du kan ta bort det negativa tecknet och parentesen från ekvationen och ersätta hakparentesen med en rund parentes.

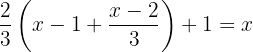
Använd distributiva lagen för att lösa upp parenteserna.

Bra att veta: När du multiplicerar ett bråk med ett annat måste du multiplicera täljare med täljare och nämnare med nämnare.

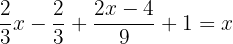
För att eliminera nämnarna måste du hitta den minsta gemensamma multipeln av och .

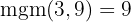
Samla lika termer:

Addera och lös ut x: