Ett av de enklaste och mest användbara koncepten är att lära sig hur man löser linjära och kvadratiska ekvationer. Dessa är de två huvudtyperna av ekvationer som ligger till grund för alla andra ekvationer med komplexa tal, t.ex. kubiska ekvationer, kvadratiska ekvationer, hyperbler och parabler.
Även om det kan vara ganska svårt för en elev att förstå dessa ekvationer, är det viktigt att komma ihåg att de ligger till grund för nästan alla avancerade kurvundersökningar. Därför är det viktigt att behärska teknikerna för att lösa problem inom detta område.
En linjär ekvation är en ekvation vars lösning endast innehåller en variabel xxx. En kvadratisk ekvation är motsatsen till en linjär ekvation. Lösningen av en linjär ekvation är alltid summan av dess variabler, medan lösningarna till en kvadratisk ekvation alltid är lika med värdena av deras respektive första gradens variabler. Lösningarna av tredje gradens ekvationer är också lika med värdena av deras respektive variabler, vilket dock är ovanligt.
I allmänhet följer du dessa steg för att lösa en linjär ekvation:
- Lös upp parenteser.
- Eliminera nämnare.
- Samla alla termer med
 på ena sidan och alla konstanta termer på den andra.
på ena sidan och alla konstanta termer på den andra. - Förenkla ekvationen.
- Lös ut den obekanta.
Exempel:
Lös 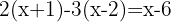
1. Lös parenteserna:
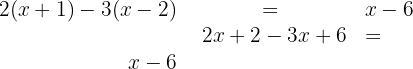
2. Samla alla termer med  på ena sidan och de konstanta termerna på den andra:
på ena sidan och de konstanta termerna på den andra:
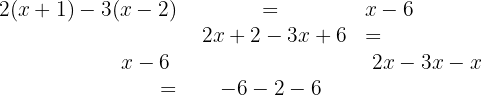
3. Förenkla liknande termer:
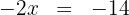
4. Lös ut  :
:
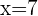
Exempel med bråktal:
Lös 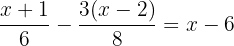
1. Lös parenteserna:
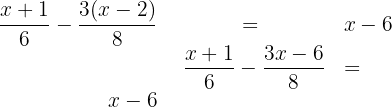
2. Eliminera nämnarna genom att multiplicera båda sidor med 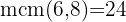 :
:
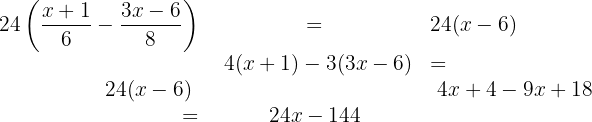
3. Samla alla x-termer på ena sidan och de konstanta på den andra:
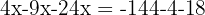
4. Förenkla liknande termer:
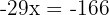
5. Lös ut  :
:
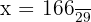
Sammanfatta med AI:


