Definition av logaritm
Den exponent som en grund måste upphöjas till för att ge ett bestämt tal. En logaritm bestämmer exponenten 
för en grund 
som användes för att erhålla ett visst resultat 
.
Exempel:
Om grunden 
och resultatet 
, vilken exponent måste talet 
ha för att resultatet ska bli 
? Som du ser är värdet på exponenten som användes för att få resultatet med grunden lika med 
.
En logaritm noteras på följande sätt:
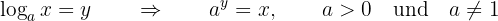
Här är grunden, resultatet och den sökta exponenten. Grunden måste vara positiv och 
och skild från 1.
Anhand der Definition des Logarithmus ergibt sich:
- Det finns ingen logaritm till en negativ grund.
- Det finns ingen logaritm av ett negativt tal.
- Det finns ingen logaritm av noll.
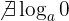
- Logaritmen av 1 är 0.
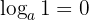
- Logaritmen av med grunden är lika med
.
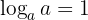
- Logaritmen med grunden av en potens med grunden är lika med exponenten.
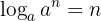
Egenskaper hos logaritmer
1 Logaritmen av en produkt är lika med summan av logaritmerna av faktorerna:
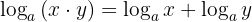
Exempel:
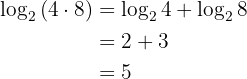
2 Logaritmen av en kvot är lika med logaritmen av täljaren minus logaritmen av nämnaren:
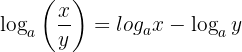
Exempel:
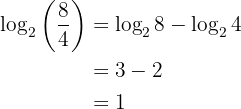
3 Logaritmen av en potens är lika med produkten av exponenten och logaritmen av grunden:
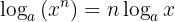
Exempel:
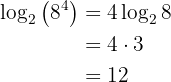
4 Logaritmen av en rot är lika med kvoten av logaritmen av radikanden och rotexponenten:
Exempel:
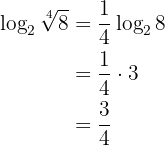
5 Basbyte:
Exempel:
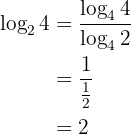
Sedan sitt uppkomst har logaritmer blivit ett viktigt verktyg för beräkningar med mycket stora tal, eftersom de har egenskapen att arbeta med exponenter och göra multiplikation till addition. Logaritmen möjliggör tack vare sina egenskaper också förenkling av olika matematiska operationer. Det lönar sig därför att närmare studera logaritmen.
Gillade du den här artikeln? Betysätt den!
Loading...