Kapitel

Substitutionsmetoden för ekvationssystem
Substitutionsmetoden består, som namnet antyder, i att sätta in värdet från en av de två ekvationerna i ett linjärt ekvationssystem i den andra ekvationen.
OBS
Om ett ekvationssystem innehåller fler variabler (obekanta) än antalet ekvationer, har det oändligt många lösningar, det vill säga varje variabel kan anta olika värden som uppfyller ekvationen. Varje variabel kan anta oändligt många lösningar. Exempel:
Givet ekvationen
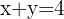
Det är en ekvation med två variabler. Vi kan snabbt se några värden för vilka ekvationen går upp:
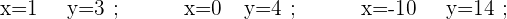

Man ser att det finns oändligt många värden för  och
och  som uppfyller ekvationen.
som uppfyller ekvationen.
Om tvärtom ett ekvationssystem har lika många ekvationer som obekanta, finns det i regel en enda lösning.
Substitutionsmetoden - Exempel: Ekvationssystem med 2 ekvationer och 2 obekanta

A 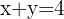 betecknar vi som "Ekvation I"
betecknar vi som "Ekvation I"
y  betecknar vi som "Ekvation II"
betecknar vi som "Ekvation II"
Lös ut en godtycklig variabel i en godtycklig ekvation. Ta alltid den variabel som kräver minst räknearbete. I detta fall är det lämpligt att lösa ut  i ekvation I:
i ekvation I:
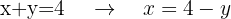
Du erhåller "värdet av  uttryckt i
uttryckt i  "
"
Sätt in det erhållna värdet i den andra ekvationen. I detta fall sätter du alltså in värdet av  i ekvation II:
i ekvation II:
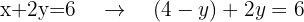
Ekvationen innehåller nu endast variabeln  . Förenkla ekvationen så att ett exakt värde för
. Förenkla ekvationen så att ett exakt värde för  står kvar.
står kvar.
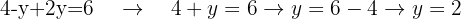
Så snart du har bestämt värdet för en av variablerna (i detta fall  ), kan du sätta in det i en av de båda ursprungliga ekvationerna för att bestämma värdet av den andra variabeln (i detta fall
), kan du sätta in det i en av de båda ursprungliga ekvationerna för att bestämma värdet av den andra variabeln (i detta fall  ).
).
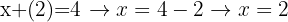
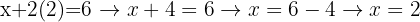
Du kan också direkt använda ekvationen som du fick när du löste ut x, eftersom du då snabbast får värdet av x:
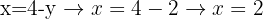
Så kan du enkelt beräkna värdena av variablerna i ett ekvationssystem med en enda lösning.
Räknesteg för att lösa ekvationssystem med 3 obekanta
1 Välj en variabel och lös ut den i en av ekvationerna:
I regel tar man variabeln med den minsta koefficienten från den enklaste ekvationen för att spara onödigt räknearbete.
2 Sätt in värdet i de andra ekvationerna:
Använd värdet som du fick när du löste ut variabeln för att sätta in det i de andra två ekvationerna. De två nya ekvationerna som du får vid insättningen bildar ett nytt ekvationssystem med två ekvationer.
3 Lös ekvationssystemet:
Upprepa därför proceduren:
- Välj en av de båda variablerna och lös ut den i en av ekvationerna.
- Sätt in det erhållna värdet i den andra ekvationen i det nya ekvationssystemet.
- Du får en linjär ekvation med en variabel och erhåller dess värde genom att lösa ut den.
- Sätt in det erhållna värdet i den andra ekvationen i det nya ekvationssystemet för att erhålla värdet av den andra variabeln.
4 Bestäm den ännu saknade variabeln:
Eftersom du i steg 3 har erhållit värdena av 2 av variablerna, sätter du nu in dessa i ekvationen i det ursprungliga ekvationssystemet där du löste ut den första variabeln.
Blandade uppgifter

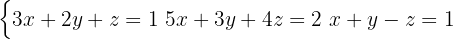
För att tillämpa substitutionsmetoden väljer du en ekvation och en variabel som du vill lösa ut. Eftersom utlösningen ska vara så enkel som möjligt är det lämpligt att ta den tredje ekvationen som har den minsta koefficienten och lösa ut 

Sätt in värdet som du fick när du löste ut i de andra två ekvationerna.








Du erhåller ett nytt ekvationssystem med 2 ekvationer
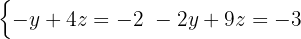
Här måste substitutionsmetoden tillämpas igen, det vill säga lösa ut en variabel i en av ekvationerna. Denna gång är  det enklaste alternativet.
det enklaste alternativet.

Sätt in det erhållna uttrycket i den andra ekvationen:




Eftersom vi har z=1 som lösning, sätt in värdet av z i den senaste ekvationen som uppstod när vi löste ut y:

Nu saknas bara värdet av  . Gå därför tillbaka till den första ekvationen som du fick när du löste ut x och sätt in de båda kända värdena där:
. Gå därför tillbaka till den första ekvationen som du fick när du löste ut x och sätt in de båda kända värdena där:
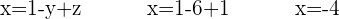

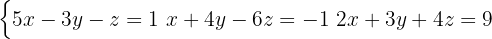
För att tillämpa substitutionsmetoden väljer du en ekvation och en variabel som du vill lösa ut. Eftersom utlösningen ska vara så enkel som möjligt är det lämpligt att ta den andra ekvationen som har den minsta koefficienten och lösa ut 

Sätt in värdet som du fick när du löste ut i de andra två ekvationerna.








Du erhåller ett nytt ekvationssystem med 2 ekvationer
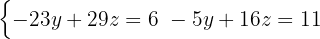
Här måste substitutionsmetoden tillämpas igen, det vill säga lösa ut en variabel i en av ekvationerna. Denna gång är  det enklaste alternativet.
det enklaste alternativet.
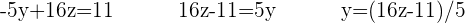
Sätt in det erhållna uttrycket i den andra ekvationen: För att ta bort nämnaren, multiplicera ekvationen med 5:





Eftersom vi har  som lösning, sätt in värdet av z i den senaste ekvationen som uppstod när vi löste ut y:
som lösning, sätt in värdet av z i den senaste ekvationen som uppstod när vi löste ut y:
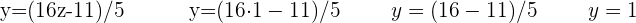
Nu saknas bara värdet av  . Gå därför tillbaka till den första ekvationen som du fick när du löste ut x och sätt in de båda kända värdena där:
. Gå därför tillbaka till den första ekvationen som du fick när du löste ut x och sätt in de båda kända värdena där:



För att tillämpa substitutionsmetoden väljer du en ekvation och en variabel som du vill lösa ut. Eftersom utlösningen ska vara så enkel som möjligt är det lämpligt att ta den första ekvationen som har den minsta koefficienten och lösa ut 

Sätt in värdet som du fick när du löste ut i de andra två ekvationerna.








Du erhåller ett nytt ekvationssystem med 2 ekvationer
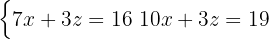
Här måste substitutionsmetoden tillämpas igen, det vill säga lösa ut en variabel i en av ekvationerna. Denna gång är  det enklaste alternativet.
det enklaste alternativet.

Sätt in det erhållna uttrycket i den andra ekvationen:







Eftersom vi har  som lösning, sätt in värdet i den senaste ekvationen som uppstod när vi löste ut
som lösning, sätt in värdet i den senaste ekvationen som uppstod när vi löste ut  :
:

Nu saknas bara värdet av  . Gå därför tillbaka till den första ekvationen som du fick när du löste ut y och sätt in de båda kända värdena där:
. Gå därför tillbaka till den första ekvationen som du fick när du löste ut y och sätt in de båda kända värdena där:
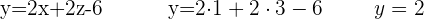
En kund i en mataffär har vid sitt inköp betalat  € för
€ för  mjölk,
mjölk,  skinka och
skinka och  olivolja. Beräkna priset för varje produkt om
olivolja. Beräkna priset för varje produkt om  olivolja kostar tre gånger så mycket som
olivolja kostar tre gånger så mycket som  mjölk och
mjölk och  skinka kostar lika mycket som
skinka kostar lika mycket som  olja plus
olja plus  mjölk.
mjölk.
Definiera variablerna: Mjölk:  Skinka:
Skinka:  Olivolja:
Olivolja: 
Från varje mening i uppgiftstexten bildar vi nu en ekvation och erhåller därigenom följande ekvationssystem:
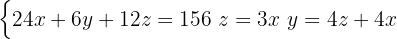
I detta fall står uttrycken för två av variablerna redan klara (ekvation 2 och 3). Sätt in uttrycket för  från den andra ekvationen i den tredje.
från den andra ekvationen i den tredje.
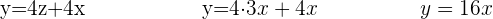
Sätt in värdena av  och
och  i den första ekvationen
i den första ekvationen





Använd ekvationerna för  och
och  för att erhålla deras värden
för att erhålla deras värden

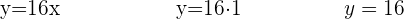
Variablerna är alltså: 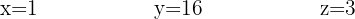
Det vill säga, priserna är: Mjölk 1 € Skinka 16 € Olivolja 3 €
En videoklubb har specialiserat sig på uthyrning av tre typer av filmer:
Barnfilmer
Vilda västern-filmer
Skräckfilmer
Det är känt att:
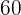 av barnfilmerna plus
av barnfilmerna plus 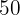 av västernfilmerna utgör
av västernfilmerna utgör  av det totala antalet filmer.
av det totala antalet filmer.
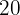 av barnfilmerna plus
av barnfilmerna plus 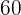 av västernfilmerna plus
av västernfilmerna plus 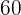 av skräckfilmerna utgör hälften av alla filmer i klubben.
av skräckfilmerna utgör hälften av alla filmer i klubben.
Det finns  fler västernfilmer än barnfilmer.
fler västernfilmer än barnfilmer.
Hur många filmer av varje genre finns det i klubben?
Tilldela varje element från uppgiften en variabel.
Barnfilmer:  Vilda västern:
Vilda västern:  Skräckfilmer:
Skräckfilmer: 
Från uppgiften får man följande ekvationssystem med tre ekvationer:
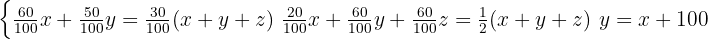
Skriv om den första ekvationen och förenkla den:

Multiplicera varje ekvation med 100 för att lösa upp nämnaren och förenkla ekvationen:



Dividera med  och du får:
och du får:

Ta den andra ekvationen och utför följande räknesteg:
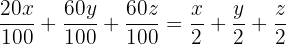
För att få bråken på samma nämnare, multiplicera höger sida av ekvationen med  och du får:
och du får:
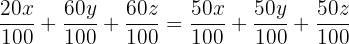
Ta bort nämnaren och förenkla:
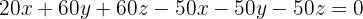
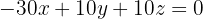
Dividera ekvationen med  :
:
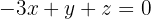
Använd de förenklade versionerna av den första och andra ekvationen och du får följande ekvationssystem:
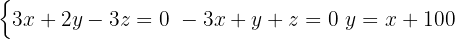
Eftersom en variabel redan står ensam, använder vi  för substitutionsmetoden i de första ursprungliga ekvationerna och multiplicerar de sistnämnda med 3.
för substitutionsmetoden i de första ursprungliga ekvationerna och multiplicerar de sistnämnda med 3.




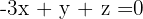
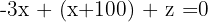
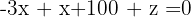

Du får ett nytt ekvationssystem med 2 ekvationer:
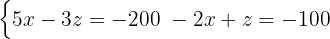
Här måste substitutionsmetoden tillämpas igen, d.v.s. lös ut en variabel i en av ekvationerna. Denna gång är  det enklaste alternativet.
det enklaste alternativet.

Sätt in det erhållna uttrycket i den andra ekvationen:





Eftersom vi har som lösning  , sätt in värdet i den sista ekvationen som uppstod vid upplösning efter
, sätt in värdet i den sista ekvationen som uppstod vid upplösning efter  :
:

Nu saknas bara värdet av  . Gå därför tillbaka till den första ekvationen som du fick vid upplösning efter y och sätt in de båda kända värdena där:
. Gå därför tillbaka till den första ekvationen som du fick vid upplösning efter y och sätt in de båda kända värdena där:
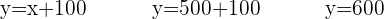
Det finns alltså:
Barnfilmer 500
Vilda västern 600
Skräckfilmer 900
Sidorna i en triangel är  ,
,  och
och 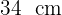 långa.
långa.
Från varje hörn ritas en cirkel. Varje cirkel tangerar de båda andra cirklarna. Beräkna radierna för de tre cirklarna.
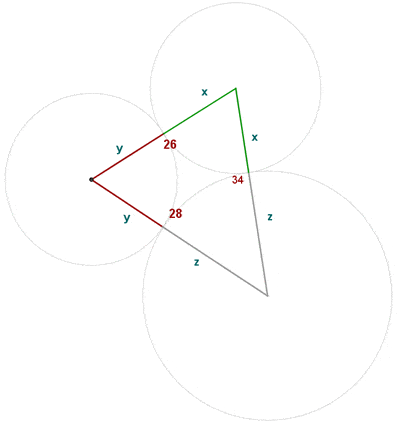
Från skissen av figuren får man följande ekvationssystem, om man använder en variabel för varje radie:
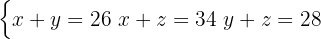
För att tillämpa substitutionsmetoden, välj en ekvation och en variabel som du vill lösa ut. I detta fall är  från den första ekvationen ett bra val:
från den första ekvationen ett bra val:

Sätt in värdet som du fick vid upplösningen i de andra två ekvationerna.





I detta fall innehåller ekvationen ingen variabel x, därför låter vi den stå kvar som den är.
Man får ett nytt ekvationssystem med två ekvationer:
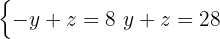
Här måste substitutionsmetoden tillämpas igen, d.v.s. lös ut en variabel i en av ekvationerna. Denna gång är  det enklaste alternativet:
det enklaste alternativet:

Sätt in det erhållna uttrycket i den andra ekvationen:






Eftersom vi har som lösning  , sätt in värdet i den sista ekvationen som uppstod vid upplösning efter
, sätt in värdet i den sista ekvationen som uppstod vid upplösning efter  :
:
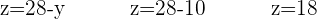
Nu saknas bara värdet av  . Gå därför tillbaka till den första ekvationen som du fick vid upplösning efter x och sätt in de båda kända värdena där:
. Gå därför tillbaka till den första ekvationen som du fick vid upplösning efter x och sätt in de båda kända värdena där:
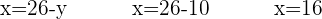
Sammanfatta med AI:












