Kapitel

Vad är en andragradsfunktion?
En andragradsfunktion är en polynomfunktion av grad 2 med formen 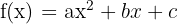 , där
, där  är reella tal och
är reella tal och 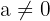 .
.
Grafen för en andragradsfunktion är alltid ett kägelsnitt (cirkel, ellips, parabel eller hyperbel), men i denna artikel behandlar vi endast andragradsfunktioner för parabler.
Grafen för  (den enklaste andragradsfunktionen) visar några egenskaper hos parabler. Bland annat är
(den enklaste andragradsfunktionen) visar några egenskaper hos parabler. Bland annat är  och
och 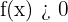 för alla andra reella värden på
för alla andra reella värden på  . Därför har funktionen ett minimum i punkten
. Därför har funktionen ett minimum i punkten  , som kallas parabelns symmetripunkt.
, som kallas parabelns symmetripunkt.
När  , är parabeln öppnad uppåt
, är parabeln öppnad uppåt
När  , är parabeln öppnad nedåt
, är parabeln öppnad nedåt
Hur löses en andragradsfunktion och hur kan den framställas?
Det finns två metoder för att lösa och framställa en andragradsfunktion. Nedan följer respektive steg:
Symmetripunktsformeln
- Bestäm värdena för
 .
. - Bestäm värdet för
 i symmetripunkten med motsvarande formel.
i symmetripunkten med motsvarande formel. - Bestäm värdet för
 genom att sätta in värdet för
genom att sätta in värdet för  .
. - Bestäm koordinaterna
 .
.
Kvadratkomplettering
Bestäm och skriv koordinaterna  .
.
Skriv ekvationen.
Dividera med värdet för termen  .
.
Flytta konstanttermen i ekvationen till höger sida.
Komplettera kvadraten på vänster sida av ekvationen.
Faktorisera vänster sida av ekvationen.
Exempeluppgifter
Bestäm symmetripunkten och ekvationen för symmetriaxeln för följande parabler
1  ;
;
2 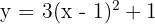 ;
;
3 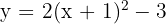 ;
;
4  ;
;
5 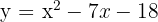 ;
;
6  ;
;
Symmetripunkten för parabeln  ges av
ges av 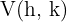 och symmetriaxeln av
och symmetriaxeln av  . För parabeln
. För parabeln 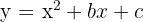 ges symmetripunkten av:
ges symmetripunkten av: 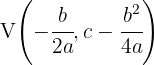
1 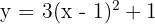

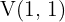

2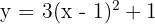
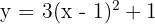
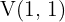

3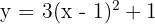
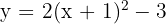

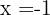
4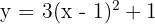



5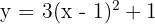
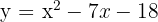
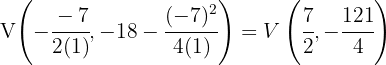
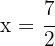
6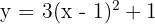

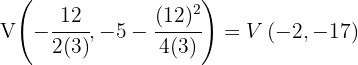

Ange, utan att rita dem, i hur många punkter följande parabler skär x-axeln
1 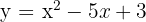 ;
;
2 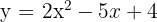 ;
;
3 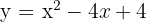 ;
;
4  .
.
Vi använder diskriminanten  och drar slutsatser från dess tecken om parablerna skär x-axeln två gånger, en gång eller inte alls.
och drar slutsatser från dess tecken om parablerna skär x-axeln två gånger, en gång eller inte alls.
1 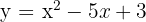 Vi beräknar diskriminanten
Vi beräknar diskriminanten

Eftersom diskriminanten är positiv finns det två skärningspunkter.
2 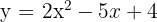
Vi beräknar diskriminanten 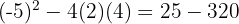
Eftersom diskriminanten är negativ finns det inga skärningspunkter.
3 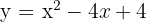
Vi beräknar diskriminanten
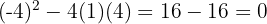
Eftersom diskriminanten är noll finns det en skärningspunkt.
4 
Vi beräknar diskriminanten
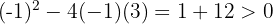
Eftersom diskriminanten är positiv finns det två skärningspunkter.
Bestäm de sökta elementen i var och en av följande funktioner
En andragradsfunktion har formen

och går genom punkten
 .
.
Beräkna värdet för  .
.
1 Vi sätter in punkten i funktionen 
2 Vi löser ut 
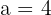
Det är känt att funktionen med formen
 går genom punkterna
går genom punkterna  och
och  .
.
Beräkna 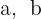 och
och  .
.
1 Vi sätter in värdet för varje punkt:


2 Vi får följande ekvationssystem

3 Vi löser systemet och får 
Symmetripunkten för en parabel är 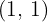 och den går genom punkten
och den går genom punkten  . Bestäm dess ekvation.
. Bestäm dess ekvation.
1 Ekvationen har formen 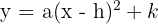
2 Vi sätter in värdena för symmetripunkten: 
3 Vi sätter in värdena för punkten  , som parabeln går genom, och bestämmer
, som parabeln går genom, och bestämmer 
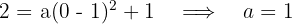
4 Vi sätter in värdet för  och beräknar
och beräknar 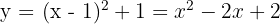
Framställ med utgångspunkt från grafen för funktionen  :
:
1 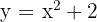 ;
;
2  ;
;
3  ;
;
4 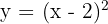 ;
;
5  ;
;
6 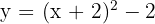 .
.
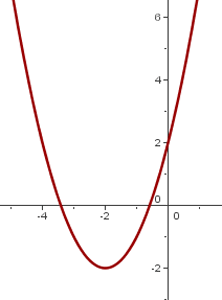
Vi utgår från grafen 
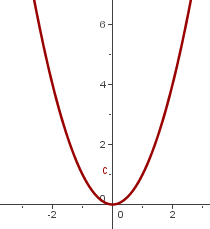
1 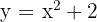
Vi förskjuter grafen för  så att symmetripunkten hamnar vid
så att symmetripunkten hamnar vid 
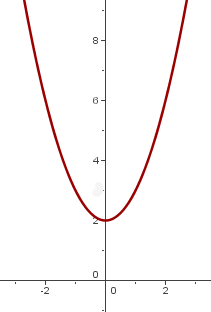
2 
Wir verschieben den Graphen von  so, dass der Scheitelpunkt sich bei
so, dass der Scheitelpunkt sich bei  befindet
befindet
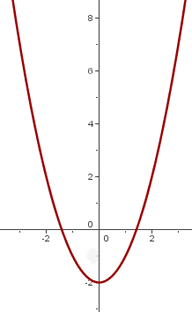
3 
Vi förskjuter symmetripunkten för  så att symmetripunkten hamnar vid
så att symmetripunkten hamnar vid 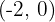
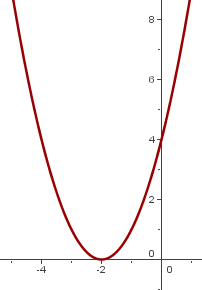
4 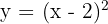
Vi förskjuter grafen för  så att symmetripunkten hamnar vid
så att symmetripunkten hamnar vid 
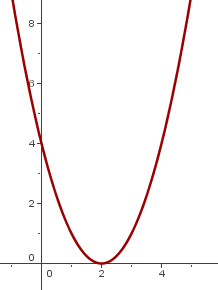
5 
Vi förskjuter grafen för  så att symmetripunkten hamnar vid
så att symmetripunkten hamnar vid 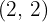
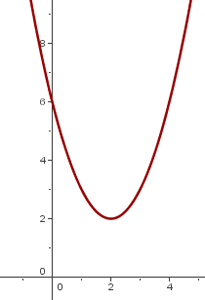
6 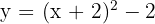
Vi förskjuter grafen för  så att symmetripunkten hamnar vid
så att symmetripunkten hamnar vid 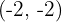
Sammanfatta med AI:












