För att kunna lösa följande uppgifter, här som påminnelse räkneregeln för logaritmer, som säger:
om 
är logaritmen av 
med basen 
,
så är omvänt 
.
Det vill säga, resultatet av logaritmeringen anger med vilken exponent man måste potensiera basen för att erhålla numerus .
Beräkna med hjälp av denna regel följande uppgifter.
Beräkna värdet av y med hjälp av logaritmregeln
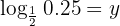
Givet är ekvationen
Man tillämpar räkneregeln för logaritmer och omvandlar 
till ett bråk, det vill säga 
, därefter förenklar man ekvationen
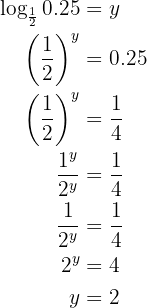
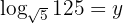
Givet är ekvationen
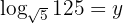
Man tillämpar räkneregeln för logaritmer och löser upp
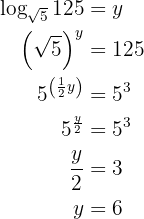
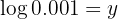
Givet är ekvationen
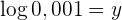
Uttrycket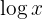 
betyder därvid alltid att 
är basen, det vill säga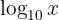 
. Man tillämpar räkneregeln för logaritmer och löser upp
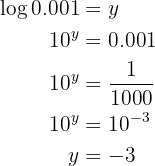
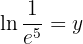
Givet är ekvationen
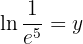
En logaritm med basen 
betecknas alltid som "naturlig logaritm" och framställs som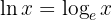 
. Man tillämpar räkneregeln för logaritmer och löser upp
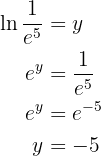
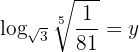
Givet är ekvationen
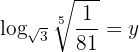
Man tillämpar räkneregeln för logaritmer och löser upp
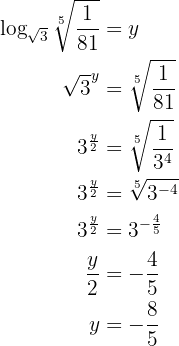
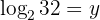
Givet är ekvationen
3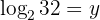
Man tillämpar räkneregeln för logaritmer och löser upp
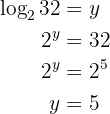
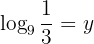
Givet är ekvationen
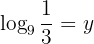
Man tillämpar räkneregeln för logaritmer och löser upp
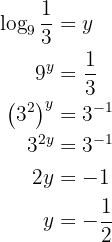
Givet är ekvationen
Man tillämpar räkneregeln för logaritmer och löser upp
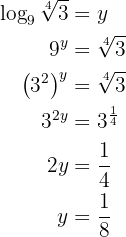
Givet är ekvationen
Man tillämpar räkneregeln för logaritmer och löser upp ekvationen. I detta fall förløper upplösningen något annorlunda, eftersom är basen för logaritmen.
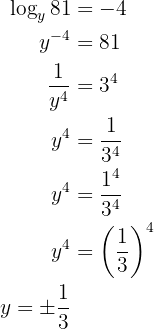
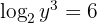
Givet är ekvationen
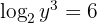
Man tillämpar räkneregeln för logaritmer och löser upp ekvationen. I detta fall förløper upplösningen något annorlunda, eftersom är en del av det logaritmiska uttrycket
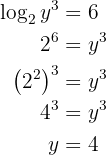
Beräkna logaritmen
I övningarna 11 till 14 tillämpar man basbyte för logaritmer, som säger att en logaritm av 
med basen är lika med
med ny bas 
. Uttrycket till höger innehåller redan den nya basen.
Givet är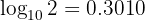 
. Beräkna följande logaritm:
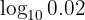
Givet är ekvationen
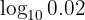
Man omvandlar det logaritmiska uttrycket till ett bråk och löser upp
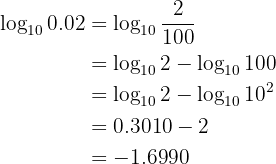
Givet är 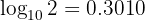. Beräkna följande logaritm:
Givet är logaritmen
Man skriver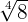 
som en potens av 
.
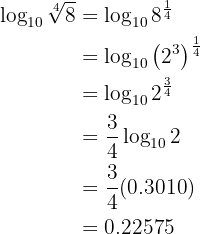
Givet är 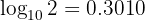. Beräkna följande logaritm:
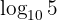
Givet är logaritmen
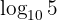
Man skriver om 
till 
och tillämpar sedan logaritmlagarna
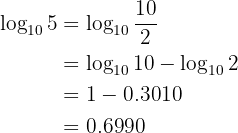
Givet är 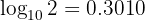. Beräkna följande logaritm:
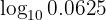
Givet är logaritmen
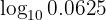
Man skriver om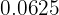 
till ett bråk med potensen och tillämpar sedan logaritmlagarna
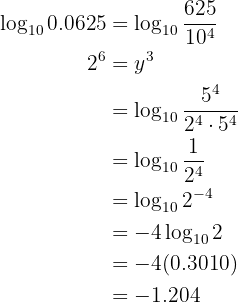
Skriv om logaritmen
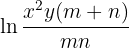
Givet är uttrycket
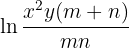
Man löser övningen enligt följande:
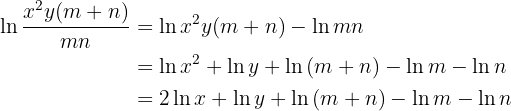
Givet är uttrycket
Man löser övningen enligt följande:
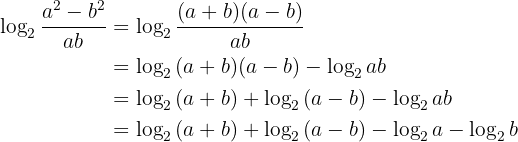
Givet är uttrycket
Man löser övningen enligt följande:
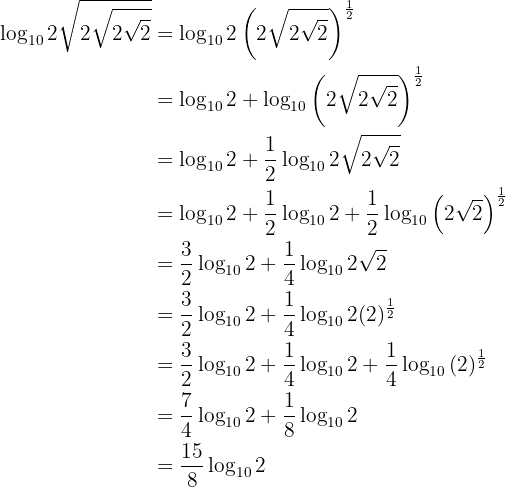
Man erhåller värdet av genom att tillämpa logaritmer
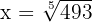
Givet är ekvationen
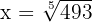
Man löser övningen enligt följande:
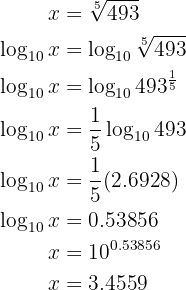
Givet är ekvationen
Man löser övningen enligt följande:
Givet är ekvationen
Man löser övningen enligt följande:
Sammanfatta med AI:
Gillade du den här artikeln? Betysätt den!
Loading...