Kapitel
Följande uppgifter behandlar teman som:
- Faktorisering av ett binom
- Faktorisering av ett perfekt kvadratiskt trinom
- Faktorisering av ett kvadratiskt trinom
- Faktorisering av ett trinom av andra graden
- Faktorisering av ett polynom av fjärde graden
- Faktorisering av ett ofullständigt polynom av tredje graden
- Faktorisering genom justering av ekvationens grad

Polynomfaktorisering och bestämning av nollställen: Uppgifter
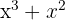
1 För att faktorisera 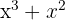 , observera att
, observera att  är en gemensam faktor för båda termerna
är en gemensam faktor för båda termerna
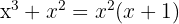
2 För att hitta roten (=nollstället) måste värdet av  väljas så att ekvationen blir noll. För
väljas så att ekvationen blir noll. För 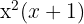 gäller detta i två fall: när
gäller detta i två fall: när  och när
och när 
Följaktligen är rötterna  och
och 
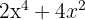
1 För att faktorisera 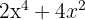 , observera att
, observera att 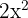 är en gemensam faktor för båda termerna
är en gemensam faktor för båda termerna
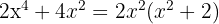
2 I detta fall är  det enda nollstället, eftersom polynomet
det enda nollstället, eftersom polynomet  inte har några rötter, d.v.s. det finns inget reellt tal
inte har några rötter, d.v.s. det finns inget reellt tal  för vilket
för vilket 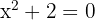 skulle gälla
skulle gälla

1 Använd konjugatregeln
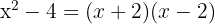
2 Rötterna, för vilka varje faktor blir noll, är
 och
och 
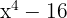
1 Använd konjugatregeln

2 Använd konjugatregeln igen på den andra faktorn

3 Rötterna, för vilka varje faktor blir noll, är
 och
och 
Observera att faktorn  inte har någon reell rot
inte har någon reell rot
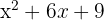
1 Här föreligger ett fullständigt kvadrattrinomium, som också kan skrivas som ett kvadratiskt binom. Ställ följande frågor:
Vilket tal i kvadrat ger  ? Och vilket tal i kvadrat ger
? Och vilket tal i kvadrat ger  ?
?
Kontrollera när den dubbla produkten av lösningarna är lika med 
2 Detta gäller för  och
och  , d.v.s. faktoriseringen måste se ut som följer
, d.v.s. faktoriseringen måste se ut som följer

3 Roten, för vilken varje faktor blir noll, är
 . Den kallas också dubbelrot
. Den kallas också dubbelrot

1 Använd i detta fall den allmänna formeln för andragradsekvationer. För detta måste ekvationen sättas lika med noll, det vill säga  . Bestäm värdena på
. Bestäm värdena på  (nollställen till ekvationen) med hjälp av den allmänna formeln
(nollställen till ekvationen) med hjälp av den allmänna formeln
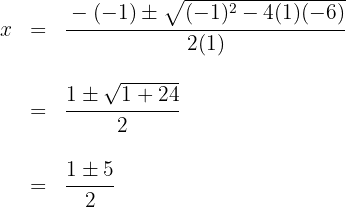
Lös ut och du får nollställena 
2 I detta fall är faktorerna till ekvationen
 .
.

1 Sätt polynomet lika med noll och genomför ett variabelbyte 
Genom att sätta in den nya variabeln får du 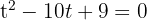
2 Lös andragradsekvationen
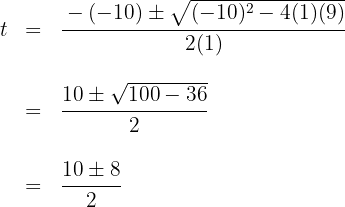
Du får nollställena 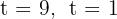
3 Genom variabelbyte får du  ; lös ut och du får nollställena
; lös ut och du får nollställena

4 I detta fall är faktorerna till ekvationen
 .
.
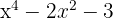
1 Sätt polynomet lika med noll och genomför ett variabelbyte 
Genom att sätta in den nya variabeln får du 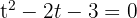
2 Lös andragradsekvationen

Du får nollställena 
3 Genom variabelbyte får du  ; lös ut och du får nollställena
; lös ut och du får nollställena
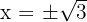 ; observera att
; observera att 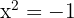 inte har några lösningar
inte har några lösningar
4 I detta fall är faktorerna till ekvationen
 .
.
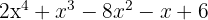
1 Hitta divisorerna till konstanttermen. Dessa är  .
.
2 Genom att använda divisionssatsen kan du avgöra för vilka värden divisionen går jämnt ut.

3 Genomför en division enligt Horners schema
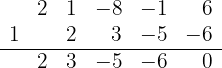
Eftersom divisionen går jämnt ut, är  ett nollställe och motsvarande polynom är
ett nollställe och motsvarande polynom är

4 Använd samma tillvägagångssätt på den andra faktorn. Pröva med  , eftersom den första faktorn kan vara en dubbelrot.
, eftersom den första faktorn kan vara en dubbelrot.

 är alltså inte ett nollställe till den andra faktorn. Pröva med
är alltså inte ett nollställe till den andra faktorn. Pröva med 
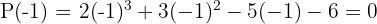
5 Genomför en division enligt Horners schema
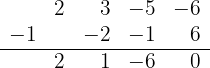
Eftersom divisionen går jämnt ut, är  ett nollställe och motsvarande polynom är
ett nollställe och motsvarande polynom är
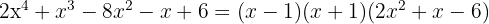
6 Bestäm nu den tredje faktorn med hjälp av andragradsekvationen eller på samma sätt som nyss, där nackdelen då är att man bara kan hitta heltalsnollställen.
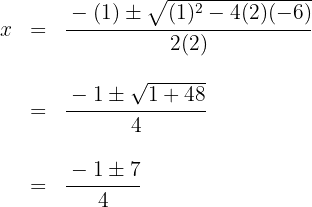
Nollställena är 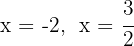 och motsvarande polynom är
och motsvarande polynom är
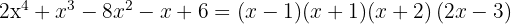

1 Hitta divisorerna till konstanttermen. Dessa är 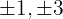 .
.
2 Genom att använda divisionssatsen kan du avgöra för vilka värden divisionen går jämnt ut.
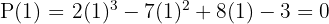
3 Genomför en division enligt Horners schema
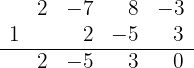
Eftersom divisionen går jämnt ut, är  ett nollställe och motsvarande polynom är
ett nollställe och motsvarande polynom är

4 Använd samma tillvägagångssätt på den andra faktorn. Pröva med  , eftersom den första faktorn kan vara en dubbelrot.
, eftersom den första faktorn kan vara en dubbelrot.

5 Genomför en division enligt Horners schema

Eftersom divisionen går jämnt ut, är  ett nollställe och motsvarande polynom är
ett nollställe och motsvarande polynom är
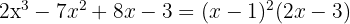
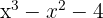
1 Hitta divisorerna till konstanttermen. Dessa är 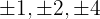 .
.
2 Genom att använda divisionssatsen kan du avgöra för vilka värden divisionen går jämnt ut.
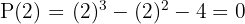
3 Genomför en division enligt Horners schema
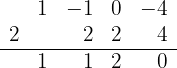
Eftersom divisionen går jämnt ut, är  ett nollställe och motsvarande polynom är
ett nollställe och motsvarande polynom är
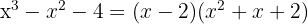
4 Bestäm nu den andra faktorn med hjälp av andragradsekvationen eller på samma sätt som nyss, där nackdelen då är att man bara kan hitta heltalsnollställen.
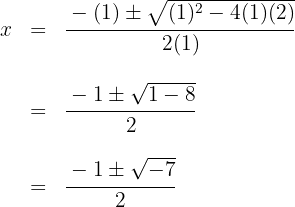
Eftersom diskriminanten är negativ, har polynomet inga reella nollställen. Därför är det enda nollstället  och motsvarande polynom är
och motsvarande polynom är
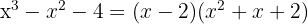
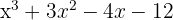
1 Hitta divisorerna till konstanttermen. Dessa är 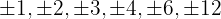 .
.
2 Genom att använda divisionssatsen kan du avgöra för vilka värden divisionen går jämnt ut.

3 Genomför en division enligt Horners schema
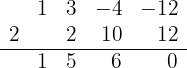
Eftersom divisionen går jämnt ut, är  ett nollställe och motsvarande polynom är
ett nollställe och motsvarande polynom är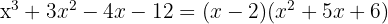
4 Bestäm nu den andra faktorn med hjälp av andragradsekvationen eller på samma sätt som nyss, där nackdelen då är att man bara kan hitta heltalsnollställen.
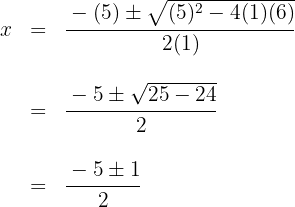
Nollställena för den andra faktorn är 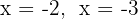 och motsvarande polynom är
och motsvarande polynom är
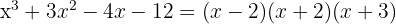
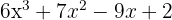
1 Hitta divisorerna till konstanttermen. Dessa är  .
.
2 Genom att använda divisionssatsen kan du avgöra för vilka värden divisionen går jämnt ut.
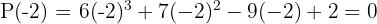
3 Genomför en division enligt Horners schema

Eftersom divisionen går jämnt ut, är  ett nollställe och motsvarande polynom är
ett nollställe och motsvarande polynom är

4 Bestäm nu den andra faktorn med hjälp av andragradsekvationen eller på samma sätt som nyss, där nackdelen då är att man bara kan hitta heltalsnollställen.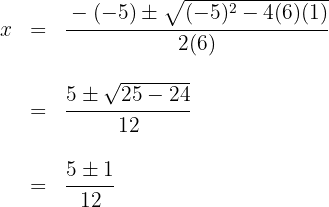
Nollställena för den andra faktorn är  och motsvarande polynom är
och motsvarande polynom är

Polynomfaktorisering: Uppgifter


Steg 1: Faktorisera ut den gemensamma faktorn 
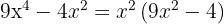
Steg 2: Skriv kvadratskillnaden som produkt av summa och differens
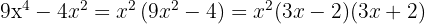
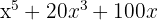
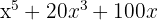
Steg 1: Faktorisera ut den gemensamma faktorn 
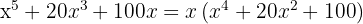
Steg 2: Identifiera det perfekta kvadratiska trinom som kan skrivas som kvadraten av ett binom
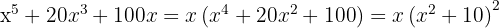
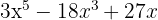
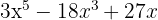
Steg 1: Faktorisera ut den gemensamma faktorn 
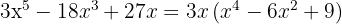
Steg 2: Identifiera det perfekta kvadratiska trinom som kan skrivas som kvadraten av ett binom
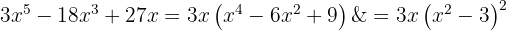
Steg 3: Skriv den kvadratiska skillnaden som summa gånger differens
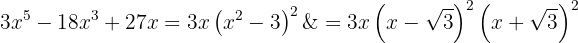
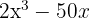
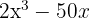
Steg 1: Faktorisera ut den gemensamma faktorn 
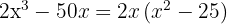
Steg 2: Skriv den kvadratiska skillnaden som summa gånger differens
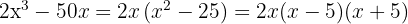
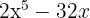
Faktorisera ut den gemensamma faktorn 
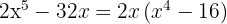
Skriv kvadratskillnaden som summa gånger differens

Den andra faktorn är ett irreducibelt polynom eller primtalsfaktor
Den tredje faktorn är en kvadratskillnad som kan skrivas som summa gånger differens
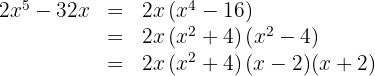
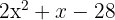
Sätt andragradstrinomet lika med noll och lös ekvationen

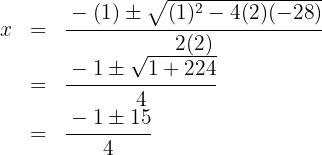
Nollställena är 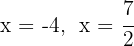 och det motsvarande polynomet kan faktoriseras som
och det motsvarande polynomet kan faktoriseras som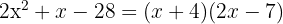
Linjär faktorisering: Uppgifter

I denna uppgift kan man faktorisera ut en gemensam faktor två gånger. Faktorisera ut  ur de två första termerna och
ur de två första termerna och  ur de två sista termerna
ur de två sista termerna

Faktorisera sedan ut den gemensamma faktorn 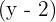



är en kvadratdifferens
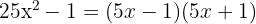
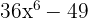
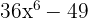
Skriv kvadratdifferensen som summa gånger differens
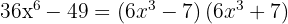

Du får ett perfekt kvadratiskt trinom som också kan skrivas som en kvadrat av ett binom.
Kvadraten av  är
är  , kvadraten av
, kvadraten av  är
är  , och det dubbla av
, och det dubbla av  gånger
gånger  är
är  .
.

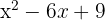
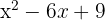
Du får ett perfekt kvadratiskt trinom som också kan skrivas som ett binoms kvadrat.
Kvadraten av  är
är  , kvadraten av
, kvadraten av  är
är  , och det dubbla av
, och det dubbla av  gånger
gånger  är
är  .
.
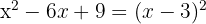

Du får ett perfekt kvadratiskt trinom som också kan skrivas som ett binoms kvadrat.
Kvadraten av  är
är  , kvadraten av
, kvadraten av  är
är  , och det dubbla av
, och det dubbla av  gånger
gånger  är
är  .
.
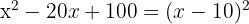


Du får ett perfekt kvadratiskt trinom som också kan skrivas som ett binoms kvadrat.
Kvadraten av  är
är  , kvadraten av
, kvadraten av  är
är  , och det dubbla av
, och det dubbla av  gånger
gånger  är
är  .
.

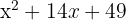
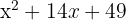
Du får ett perfekt kvadratiskt trinom som också kan skrivas som ett binoms kvadrat.
Kvadraten av  är
är  , kvadraten av
, kvadraten av  är
är  , och det dubbla av
, och det dubbla av  gånger
gånger  är
är 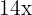 .
.
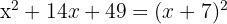
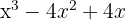
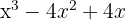
Faktorera ut den gemensamma faktorn

Du får ett ytterligare perfekt kvadratiskt trinom.
Kvadraten av  är
är  , kvadraten av
, kvadraten av  är
är  , och det dubbla av
, och det dubbla av  gånger
gånger  är
är  .
.
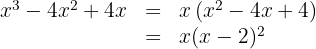


Faktorera ut den gemensamma faktorn
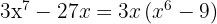
Skriv den kvadratiska differensen som en summa gånger en differens

Använd formeln för kubsumma och kubdifferens
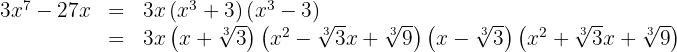
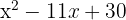
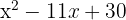
Sätt polynomet lika med noll
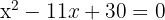
Lös andragradsekvationen
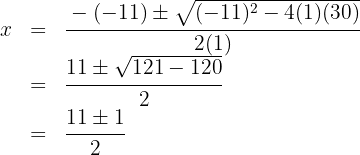
Nollställena är 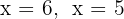 och motsvarande polynom är
och motsvarande polynom är



Lös andragradsekvationen
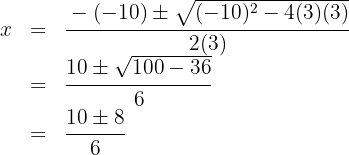
Nollställena är 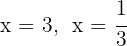 och motsvarande polynom är
och motsvarande polynom är
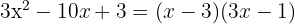
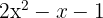
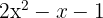
Lös andragradsekvationen
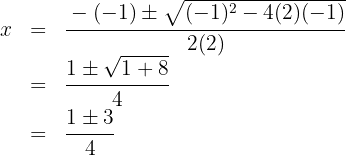
Nollställena är 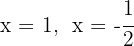 och motsvarande polynom är
och motsvarande polynom är

Sammanfatta med AI:












