Potensräkning: blandade uppgifter

För att multiplicera potenser med samma bas låter vi basen stå kvar och adderar exponenterna:

För att dividera potenser med samma bas låter vi basen stå kvar och subtraherar exponenterna:

För att beräkna en potens av en potens multiplicerar vi exponenterna med varandra:

För att beräkna potensen av en produkt använder vi samma exponent för båda baserna:

För att beräkna en potens av en potens multiplicerar vi exponenterna med varandra:

För att beräkna en potens av en potens multiplicerar vi exponenterna med varandra.

Skriv först basen som en produkt av primtal. Hitta sedan potensen av potensen genom att multiplicera exponenterna:

Skriv först basen som en produkt av primtal. Beräkna sedan potensen av potensen genom att multiplicera exponenterna:

För att multiplicera potenser med samma bas låter vi basen stå kvar och adderar exponenterna:

För att dividera potenser med samma bas låter vi basen stå kvar och subtraherar exponenterna:

För att beräkna en potens av en potens multiplicerar vi exponenterna med varandra:

För att beräkna potensen av en produkt använder vi samma exponent för båda faktorerna:

För att beräkna en potens av en potens multiplicerar vi exponenterna med varandra:

För att beräkna en potens av en potens multiplicerar vi först exponenterna med varandra. Tänk på att alla tal som är olika noll och har exponent noll ger resultatet 1:

Skriv först basen som en produkt av primtal. Beräkna sedan potensen av potensen genom att multiplicera exponenterna:

Skriv först basen som en produkt av primtal. Beräkna sedan potensen av potensen genom att multiplicera exponenterna:

För att multiplicera potenser med samma bas låter vi basen stå kvar och adderar exponenterna:

Resultatet måste ha ett negativt tecken, eftersom basen är negativ och exponenten ett udda tal:

Bryt först ned talet 8 i faktorer. Multiplicera sedan potenserna med samma bas:

Resultatet måste ha ett positivt tecken, eftersom basen är negativ och exponenten ett jämnt tal:

För att multiplicera potenser med samma bas låter vi basen stå kvar och adderar exponenterna:

Resultatet måste ha ett negativt tecken, eftersom basen är negativ och exponenten ett udda tal:

För att multiplicera potenser med samma bas låter vi basen stå kvar och adderar exponenterna:

Eftersom exponenten är negativ måste vi ta inversen av basen:

För att dividera potenser med samma bas låter vi basen stå kvar och subtraherar exponenterna:

Eftersom exponenten är negativ måste vi ta basens invers:

För att dividera potenser med samma bas låter vi basen stå kvar och subtraherar exponenterna:

Eftersom exponenten är negativ måste vi ta basens invers och använda en positiv exponent:

För att dividera potenser med samma bas låter vi basen stå kvar och subtraherar exponenterna:

För att dividera potenser med samma bas låter vi basen stå kvar och subtraherar exponenterna:

För att beräkna en potens av en potens låter vi basen stå kvar och multiplicerar exponenterna med varandra:

För att dividera potenser med samma bas låter vi basen stå kvar och subtraherar exponenterna:

Förenkla först uttrycket inom parentesen. Låt basen stå kvar och subtrahera exponenterna från varandra:

För att beräkna en potens av en potens låter vi basen stå kvar och multiplicerar exponenterna med varandra:

Resultatet måste ha ett positivt tecken, eftersom basen är negativ och exponenten ett jämnt tal:

För att multiplicera potenser med samma bas låter vi basen stå kvar och adderar exponenterna:

Resultatet måste ha ett positivt tecken, eftersom basen är negativ och exponenten ett jämnt tal:

Bryt först ned talet 27 i faktorer. Multiplicera sedan potenserna med samma bas:

Resultatet måste ha ett positivt tecken, eftersom basen är negativ och exponenten ett jämnt tal:

För att multiplicera potenser med samma bas låter vi basen stå kvar och adderar exponenterna:

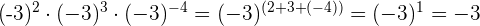
Resultatet måste ha ett negativt tecken, eftersom basen är negativ och exponenten ett udda tal:

För att multiplicera potenser med samma bas låter vi basen stå kvar och adderar exponenterna:

Eftersom exponenten är negativ måste vi ta basens invers och använda en positiv exponent:

För att dividera potenser med samma bas låter vi basen stå kvar och subtraherar exponenterna:

Eftersom exponenten är negativ måste vi ta basens invers:

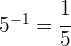
För att dividera potenser med samma bas låter vi basen stå kvar och subtraherar exponenterna:

Eftersom exponenten är negativ måste vi ta basens invers och använda en positiv exponent:

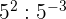
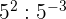
För att dividera potenser med samma bas låter vi basen stå kvar och subtraherar exponenterna:

För att dividera potenser med samma bas låter vi basen stå kvar och subtraherar exponenterna:

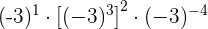
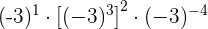
För att beräkna en potens av en potens låter vi basen stå kvar och multiplicerar exponenterna med varandra:

För att dividera potenser med samma bas låter vi basen stå kvar och subtraherar exponenterna:

Resultatet måste ha ett negativt tecken, eftersom basen är negativ och exponenten ett udda tal:

Förenkla först uttrycket inom parentesen. Låt basen stå kvar och subtrahera exponenterna från varandra:

För att beräkna en potens av en potens låter vi basen stå kvar och multiplicerar exponenterna med varandra:

Resultatet måste ha ett negativt tecken, eftersom basen är negativ och exponenten ett udda tal:

För att multiplicera potenser med samma bas låter vi basen stå kvar och adderar exponenterna:

För att multiplicera potenser med samma bas låter vi basen stå kvar och adderar exponenterna:

Eftersom potensen har exponenten 1 är potensen lika med basen:

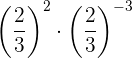
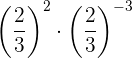
För att multiplicera potenser med samma bas låter vi basen stå kvar och adderar exponenterna:

Eftersom exponenten är negativ måste vi ta basens invers och använda en positiv exponent. Potensen som vi då får har exponenten 1, vilket betyder att potensen är lika med den nya basen:

För att multiplicera potenser med samma bas låter vi basen stå kvar och adderar exponenterna:

Eftersom exponenten är negativ måste vi ta basens invers och använda en positiv exponent:

Ta inversen av det andra elementet för att få en positiv exponent. Multiplicera sedan potenser med samma bas:

Eftersom potensen har exponenten 1 är potensen lika med basen:

För att dividera potenser med samma bas låter vi basen stå kvar och subtraherar exponenterna:

Eftersom exponenten är negativ måste vi ta basens invers och använda en positiv exponent. Potensen som vi då får har exponenten 1, vilket betyder att potensen är lika med den nya basen:

För att dividera potenser med samma bas låter vi basen stå kvar och subtraherar exponenterna:

Eftersom exponenten är negativ måste vi ta basens invers och använda en positiv exponent:

För att dividera potenser med samma bas låter vi basen stå kvar och subtraherar exponenterna:

För att dividera potenser med samma bas låter vi basen stå kvar och subtraherar exponenterna:

Potensen vi får har exponenten 1, vilket betyder att potensen är lika med den nya basen:

Bilda den reciproka vid det första elementet för att få en positiv exponent. Multiplicera sedan potenser med samma bas.

För att beräkna en potens av en potens låter vi basen stå kvar och multiplicerar exponenterna med varandra.

För att beräkna en potens av en potens låter vi basen stå kvar och multiplicerar exponenterna med varandra.

Eftersom exponenten är negativ måste vi bilda den reciproka basen med positiv exponent.

Skriv om potensernas baser som potenser av primtal.

Bilda den reciproka av det första elementet för att få en positiv exponent. Multiplicera sedan potenser med samma bas.

1 För alla bråk till samma nämnare. Faktorisera de tal som inte är primtal:

2 I uttrycket finns potenser av potenser. Behåll basen och multiplicera exponenterna:

3 Bilda för alla potenser med bas och negativ exponent den omvända potensen med positiv exponent:

4 Multiplicera potenser med samma bas i täljaren och i nämnaren. Dividera sedan resultaten. Avsluta med att bilda det omvända bråket med positiv exponent:

1 Utför först multiplikationerna och divisionerna inom parenteserna:

2 Förenkla bråken där det är möjligt, skriv om blandade tal och beräkna sedan summorna inom parenteserna:

3 Skriv om det sista uttrycket och tillämpa potenslagen för rationella tal:

4 Utför divisionerna och förenkla. Avsluta med att bilda subtraktionen av de kvarvarande bråken:

En potens med ett bråk som exponent kan skrivas som en rot: basen blir rotens radikand, nämnaren i exponenten blir exponenten på radikanden och täljaren i exponenten blir rotens exponent. Faktorisera talet 16, beräkna radikanden och ta roten:

Faktorisera talet beräkna radikanden och ta roten:

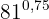
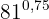
I det här fallet är exponenten ett decimaltal, som först måste skrivas om som ett bråk. Beräkna sedan radikanden och ta roten:

Exponent är ett periodiskt tal, som först måste skrivas om som ett bråk:

Skriv roten, beräkna radikanden och ta roten: