
Introduktion till proportionell tilldelning
Inom matematiken skiljer man mellan två typer av tilldelningar för att visa förhållandet mellan två värden:
1. Proportionell tilldelning: enligt mönstret "ju mer, desto mer"
2. Omvänt proportionell tilldelning: enligt mönstret "ju mer, desto mindre"
För att visa tilldelningar visuellt använder man pildiagram.
Blandade uppgifter

I en proportion är produkten av medelvärdena lika med produkten av yttervärden



I en proportion är produkten av medelvärdena lika med produkten av yttervärden

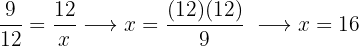
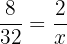
I en proportion är produkten av medelvärdena lika med produkten av yttervärden
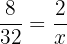
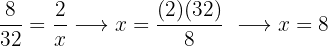
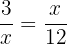
I en proportion är produkten av medelvärdena lika med produkten av yttervärden
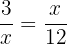
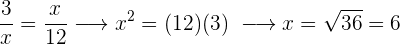

I en proportion är produkten av medelvärdena lika med produkten av yttervärden
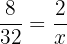
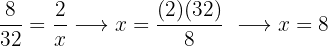
Räkneuppgift: Varv
Två hjul är sammankopplade med en drivrem. Det första hjulet har en radie på 25 cm, det andra på 75 cm. Hur många gånger har det andra hjulet vridit sig när det första har gjort 300 varv?
Det handlar här om en omvänt proportionell tilldelning, eftersom hjulens varv blir färre ju större deras radie är.
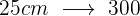 varv
varv
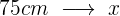 varv
varv
Följande formel gäller för omvänt proportionell tilldelning
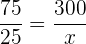
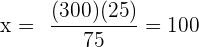 varv
varv
Räkneuppgift: Hotellkostnader
Vistelsen för sex personer på ett hotell kostar 792 € i 12 dagar. Hur mycket kostar vistelsen för 15 personer i 8 dagar?
Ju fler personer som bor på hotellet, desto mer kostar vistelsen. Det handlar här alltså om en proportionell tilldelning.
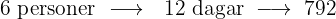 €
€
 €
€
Följande formel gäller för proportionell tilldelning
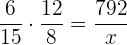
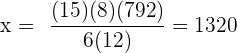 €
€
Räkneuppgift: Färghinkar
Om man kan måla ett 90 m långt och 80 cm högt staket med 12 hinkar à  färg, hur många hinkar à
färg, hur många hinkar à 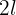 färg skulle man behöva om man ville måla ett liknande staket med
färg skulle man behöva om man ville måla ett liknande staket med  höjd och
höjd och  längd?
längd?
Ju mer kilo färg som behövs, desto färre hinkar, det vill säga det föreligger en omvänt proportionell tilldelning.
Ju mer 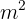 man vill måla, desto fler färghinkar behöver man, det vill säga det föreligger dessutom en proportionell tilldelning.
man vill måla, desto fler färghinkar behöver man, det vill säga det föreligger dessutom en proportionell tilldelning.
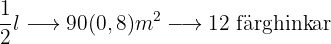
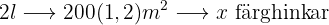
Följande formel gäller för tilldelningen
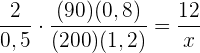
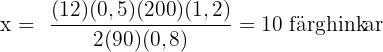
Räkneuppgift: Byggarbetare
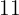 byggarbetare bearbetar en rektangulär yta på
byggarbetare bearbetar en rektangulär yta på  längd och
längd och 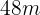 bredd inom
bredd inom  dagar. Hur många byggarbetare skulle behövas för att bearbeta en liknande yta med
dagar. Hur många byggarbetare skulle behövas för att bearbeta en liknande yta med 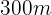 längd och
längd och  bredd på 5 dagar?
bredd på 5 dagar?
Ju mer yta, desto fler byggarbetare behövs, det vill säga det föreligger en proportionell tilldelning.
Ju fler dagar man har till förfogande, desto färre byggarbetare behöver man, det vill säga det föreligger dessutom en omvänt proportionell tilldelning.
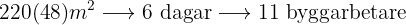
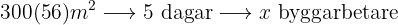
Följande formel gäller för tilldelningen
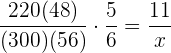
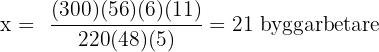
Räkneuppgift: Vattentank
Man behöver 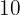 timmar för att fylla en vattentank med en kapacitet på
timmar för att fylla en vattentank med en kapacitet på 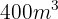 med hjälp av sex vattenslang. Hur många timmar skulle man behöva för att fylla
med hjälp av sex vattenslang. Hur många timmar skulle man behöva för att fylla 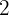 vattentankar med en kapacitet på vardera
vattentankar med en kapacitet på vardera 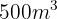 med hjälp av fyra vattenslang?
med hjälp av fyra vattenslang?
Ju fler vattenslang, desto färre timmar behöver man, det vill säga det föreligger en omvänt proportionell tilldelning.
Ju större tanken är, desto fler timmar behöver man, det vill säga det föreligger en ytterligare proportionell tilldelning.
Ju mer 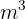 volym tanken har, desto fler timmar behöver man, det vill säga det föreligger en ytterligare proportionell tilldelning.
volym tanken har, desto fler timmar behöver man, det vill säga det föreligger en ytterligare proportionell tilldelning.
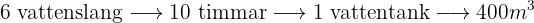
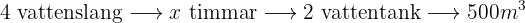
Följande formel gäller för tilldelningen
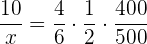
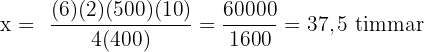
Räkneuppgift: Elever
Av  elever på ett gymnasium är
elever på ett gymnasium är 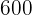 på en skolutflykt. Hur många procent av eleverna är på skolutflykten?
på en skolutflykt. Hur många procent av eleverna är på skolutflykten?
Det handlar om en proportionell tilldelning:
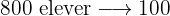 %
% 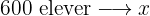
Följande formel gäller för tilldelningen
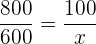
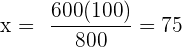 %
%
Räkneuppgift: Rabatt vid bilköp
Vid köp av ett fordon med ett pris på 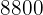 € får vi en rabatt på
€ får vi en rabatt på 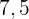 %. Hur mycket måste vi betala för fordonet?
%. Hur mycket måste vi betala för fordonet?
Börja med tilldelningen på följande sätt:
 €
€ 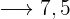 €
€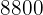 €
€ 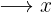
Följande formel gäller för tilldelningen
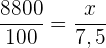
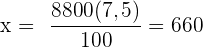 €
€
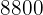 € -
€ -  €
€ 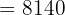 €
€
Uppgiften kan också beräknas på ett mer direkt sätt:
Det föreligger en rabatt på 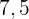 %, det vill säga per
%, det vill säga per  € betalar man
€ betalar man 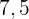 € mindre. Istället för
€ mindre. Istället för  € betalar vi alltså
€ betalar vi alltså 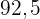 €.
€.
 €
€ 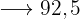 €
€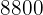 €
€ 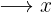
Följande formel gäller för tilldelningen
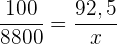
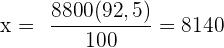 €
€
Räkneuppgift: Moms vid datorköp
En dator kostar  € (exkl. moms). Hur mycket måste man betala totalt om momsen är
€ (exkl. moms). Hur mycket måste man betala totalt om momsen är  %?
%?
Momsen ligger på  %, det vill säga per
%, det vill säga per  € betalar man
€ betalar man 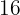 mer. Istället för
mer. Istället för  € betalar man alltså
€ betalar man alltså 
 €
€ 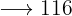 €
€ €
€ 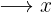 €
€
Följande formel gäller för tilldelningen
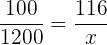
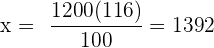 €
€
Räkneuppgift: Rabatt vid köp av en bildskärm
Vid köp av en bildskärm med ett pris på  € får vi en rabatt på
€ får vi en rabatt på 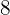 . Hur mycket måste vi betala?
. Hur mycket måste vi betala?
Vi får en rabatt på 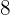 %, det vill säga per
%, det vill säga per  € betalar vi
€ betalar vi 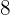 € mindre. Istället för
€ mindre. Istället för  € betalar vi alltså bara
€ betalar vi alltså bara  €.
€.
Lösning: €
€ 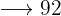 €
€ €
€ 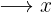
Följande formel gäller för tilldelningen
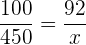
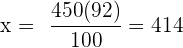 €
€
Räkneuppgift: Vinst vid försäljning
Ett varuhus säljer en artikel med 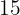 % vinst jämfört med inköpspriset. Inköpspriset var
% vinst jämfört med inköpspriset. Inköpspriset var 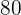 €. Bestäm försäljningspriset.
€. Bestäm försäljningspriset.
Den önskade vinsten ligger på 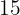 % jämfört med inköpspriset, det vill säga per
% jämfört med inköpspriset, det vill säga per  € måste slutkunden alltså betala
€ måste slutkunden alltså betala 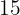 € mer. Istället för
€ mer. Istället för  € måste hen betala
€ måste hen betala 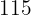 €.
€.
 €
€ 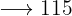 €
€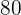 €
€ 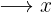
Följande formel gäller för tilldelningen
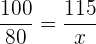
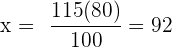 €
€
Räkneuppgift I: Försäljning av en artikel
Vilket försäljningspris måste stå på prislappen för en artikel som har kostat 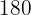 € i inköp, för att göra
€ i inköp, för att göra 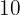 % vinst vid försäljningen?
% vinst vid försäljningen?
Om inköpspriset ligger på  € och
€ och 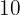 % vinst ska uppnås, måste försäljningspriset ligga på
% vinst ska uppnås, måste försäljningspriset ligga på 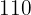 €.
€.
Försäljning Inköp
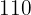 €
€ 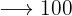 €
€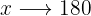 €
€
Följande formel gäller för tilldelningen

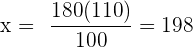 €
€
Räkneuppgift II: Försäljning av en artikel
En artikel köptes in för  € och såldes med
€ och såldes med 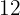 % förlust. Vilket pris står på försäljningsskylt?
% förlust. Vilket pris står på försäljningsskylt?
Om försäljningspriset ligger på  € och man gör
€ och man gör 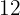 % förlust, låg inköpspriset på
% förlust, låg inköpspriset på  €.
€.
Försäljning Inköp
 €
€ 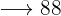
 €
€ 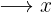
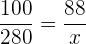
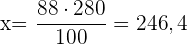 €
€
Räkneuppgift III: Försäljning av en artikel
Vid försäljning av ett objekt görs 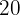 % förlust jämfört med inköpspriset. Till vilket pris säljs objektet om inköpspriset var
% förlust jämfört med inköpspriset. Till vilket pris säljs objektet om inköpspriset var 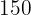 €.
€.
Om inköpspriset ligger på  € och man gör
€ och man gör 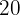 % förlust, ligger försäljningspriset på
% förlust, ligger försäljningspriset på 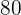 €.
€.
Inköp Försäljning
 €
€ 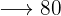
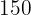 €
€ 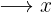
Följande formel gäller för tilldelningen
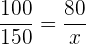
Sammanfatta med AI:












