Välkommen till vår sida med uppgifter och problem som löses med proportionsräkning! Proportionsräkning är ett av de mest praktiska och användbara verktygen inom matematiken för att bestämma förhållanden mellan olika objekt. Det fungerar som en kompass som leder oss genom situationer där vi behöver relatera mängder och hitta exakta proportioner.
Här presenterar vi olika övningar och problem som hjälper dig att fördjupa dina färdigheter inom detta område. Oavsett om du vill förbättra dina vardagliga matematiska färdigheter eller använda proportionsräkning i mer komplexa sammanhang, är du på rätt plats – förbered dig på att utmana ditt sinne och bli en expert på proportionsräkning!
Två hjul är förbundna med ett drivrem. Det första hjulet har en radie på  cm och det andra på
cm och det andra på  cm. Om det första hjulet har gjort
cm. Om det första hjulet har gjort  varv, hur många varv gör då det andra hjulet?
varv, hur många varv gör då det andra hjulet?
Först och främst är dessa storheter omvänt proportionella, eftersom ju större radien är, desto färre varv gör hjulet. Om  är det sökta antalet varv, får vi följande diagram:
är det sökta antalet varv, får vi följande diagram:

Förhållandet mellan varven är lika med förhållandet mellan radierna:
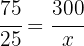
Alltså är värdet på 
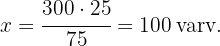
Skalan på en karta är följande:  cm på kartan motsvarar
cm på kartan motsvarar 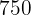 m i verkligheten. Hur många meter motsvarar
m i verkligheten. Hur många meter motsvarar  cm på kartan i verkligheten?
cm på kartan i verkligheten?
Först och främst måste man notera att det handlar om direkt proportionella storheter, det vill säga ju fler centimeter på kartan, desto fler meter i verkligheten. Om  är antalet meter i verkligheten, får vi följande diagram:
är antalet meter i verkligheten, får vi följande diagram:
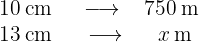
Förhållandet mellan meter är lika med förhållandet mellan centimeter på följande sätt:
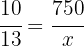
Alltså är värdet på  :
:
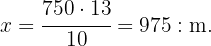
Sex personer kan stanna i ett hotell i  dagar och betalar
dagar och betalar 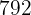 €. Hur mycket kostar det för
€. Hur mycket kostar det för  personer att stanna åtta dagar på samma hotell?
personer att stanna åtta dagar på samma hotell?
Ju fler personer, desto högre kostnad, och ju fler dagar, desto högre kostnad, det vill säga storheterna är direkt proportionella. Låt  vara det sökta kostnadsvärdet, då:
vara det sökta kostnadsvärdet, då:
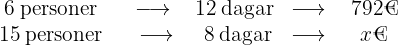
Därför är produkten av förhållandet för personer och förhållandet för dagar lika med förhållandet för pengar, det vill säga:
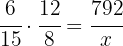
Nu bestämmer vi värdet på  :
:
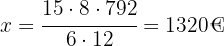
Alltså kostar hotellet för  personer under åtta dagar
personer under åtta dagar 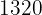 €.
€.
En butik tar ut 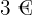 för en insättning på
för en insättning på  . Om beloppet inte är exakt, beräknas avgiften proportionellt. Om en person sätter in
. Om beloppet inte är exakt, beräknas avgiften proportionellt. Om en person sätter in 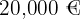 , hur mycket tar butiken då ut för insättningen?
, hur mycket tar butiken då ut för insättningen?
Först och främst handlar det om direkt proportionella storheter, eftersom ju mer pengar som skickas, desto högre blir avgiften. Om  är beloppet som tas ut för pengarna, får vi följande diagram:
är beloppet som tas ut för pengarna, får vi följande diagram:

Förhållandet mellan avgiften är lika med förhållandet mellan det insatta beloppet på följande sätt:
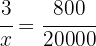
Alltså är värdet på  :
:
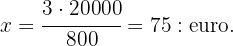
Om  burkar à
burkar à 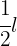 färg används för att måla
färg används för att måla  m av ett
m av ett  cm högt staket: Beräkna hur många
cm högt staket: Beräkna hur många 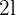 burkar som behövs för att måla ett liknande staket med
burkar som behövs för att måla ett liknande staket med  cm höjd och
cm höjd och  m längd.
m längd.
Ju mer färg varje burk innehåller, desto färre burkar behövs. Storheterna är omvänt proportionella. Ju större yta som ska målas, desto fler burkar behövs. Det handlar om direkt proportionella storheter, och denna information gör det möjligt att skapa följande diagram:
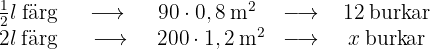
I detta fall är  antalet färgburkar som behövs. I den mittersta kolumnen har vi omvandlat stakets längd till meter och beräknat ytan genom att multiplicera höjd med längd.
antalet färgburkar som behövs. I den mittersta kolumnen har vi omvandlat stakets längd till meter och beräknat ytan genom att multiplicera höjd med längd.
Nu bestämmer vi värdet på  med följande ekvation:
med följande ekvation:
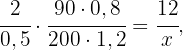
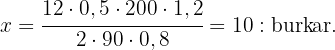
Det tar  dagar för
dagar för  arbetare att bygga ett hus. Hur många dagar skulle det ta om
arbetare att bygga ett hus. Hur många dagar skulle det ta om  extra arbetare fanns tillgängliga?
extra arbetare fanns tillgängliga?
Först måste man notera att antalet arbetare är omvänt proportionellt mot antalet dagar, eftersom det är uppenbart att ju fler arbetare som arbetar, desto mindre tid tar byggandet av huset. Om  är det sökta antalet dagar, får vi följande diagram:
är det sökta antalet dagar, får vi följande diagram:
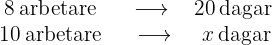
Förhållandet mellan antalet arbetare och antalet dagar är invers:
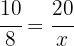
Alltså är värdet på  :
:
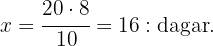
 arbetare plöjer ett rektangulärt fält med
arbetare plöjer ett rektangulärt fält med 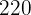 m längd och
m längd och  m bredd på
m bredd på  dagar. Hur många arbetare behövs för att plöja ett liknande fält med
dagar. Hur många arbetare behövs för att plöja ett liknande fält med  m längd och
m längd och 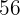 m bredd på fem dagar?
m bredd på fem dagar?
Ju större yta, desto fler dagar behövs. Storheterna är direkt proportionella. Ju fler dagar, desto färre arbetare behövs. Dessa storheter är omvänt proportionella. Detta ger följande diagram:
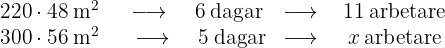
I diagrammet i första kolumnen har vi beräknat fältets yta genom att multiplicera bredden med längden. Nu måste vi bestämma värdet på  med följande ekvation:
med följande ekvation:

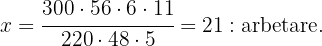
Det betyder att  arbetare behövs för att plöja fältet med
arbetare behövs för att plöja fältet med  m längd och
m längd och 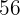 m bredd på fem dagar.
m bredd på fem dagar.
 vårdare tar hand om
vårdare tar hand om  patienter på
patienter på  dagar. Hur många vårdare behövs för att ta hand om
dagar. Hur många vårdare behövs för att ta hand om  patienter på
patienter på  dagar?
dagar?
Först: Ju fler vårdare, desto färre dagar behövs för att ta hand om patienterna, alltså är variabeln dagar invers. På samma sätt: Ju fler patienter, desto fler vårdare behövs, alltså är variabeln patienter direkt proportionell. Om  är det sökta antalet vårdare, kan problemet illustreras på följande sätt:
är det sökta antalet vårdare, kan problemet illustreras på följande sätt:
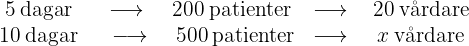
Därför är det omvända förhållandet för dagarna multiplicerat med förhållandet för patienterna lika med förhållandet för vårdarna, eftersom dagarna är omvänt proportionella och patienterna direkt proportionella, det vill säga:
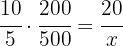
Nu bestämmer vi värdet på  :
:
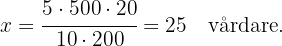
Sex vattenkranar behöver  timmar för att fylla en tank med volym
timmar för att fylla en tank med volym  . Hur många timmar behöver fyra vattenkranar för att fylla
. Hur många timmar behöver fyra vattenkranar för att fylla  tankar med vardera
tankar med vardera  ?
?
Ju fler vattenkranar, desto färre timmar behövs. Det handlar om omvänt proportionella storheter. Ju fler tankar, desto fler timmar behövs. Det handlar om direkt proportionella storheter. Ju fler  , desto fler timmar behövs. Det handlar om direkt proportionella storheter. Med denna information kan vi skapa följande diagram:
, desto fler timmar behövs. Det handlar om direkt proportionella storheter. Med denna information kan vi skapa följande diagram:
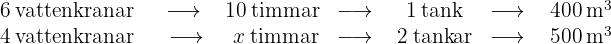
Dessa  storheter står i följande förhållande:
storheter står i följande förhållande:
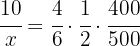
Om vi bestämmer värdet på  timmar får vi:
timmar får vi:
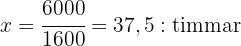
Alltså behöver fyra vattenkranar 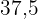 timmar för att fylla
timmar för att fylla  tankar med
tankar med  .
.
 symaskiner tillverkade igår
symaskiner tillverkade igår  plagg. Om endast
plagg. Om endast  maskiner finns tillgängliga idag, hur många plagg kommer de då att tillverka idag?
maskiner finns tillgängliga idag, hur många plagg kommer de då att tillverka idag?
Här måste man notera att variabeln "maskiner" är direkt proportionell, det vill säga om färre maskiner finns, produceras färre plagg. Om  är det sökta antalet plagg, får vi följande diagram:
är det sökta antalet plagg, får vi följande diagram:
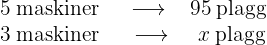
Därför är förhållandet mellan maskiner lika med förhållandet mellan plagg på följande sätt:
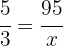
Värdet på  blir alltså:
blir alltså:
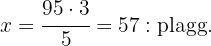
Sammanfatta med AI:


