Kapitel
- Beståndsdelar i en rot
- Potenser och rötter
- Lika rötter
- Förenkling av rötter
- Gemensam rotexponent
- Delvis rotutdragning
- Att ta in faktorer under roten
- Addition och subtraktion av rötter
- Multiplikation av rötter med samma rotexponent
- Multiplikation av rötter med olika rotexponenter
- Division av rötter med samma rotexponent
- Division av rötter med olika rotexponenter
- Potens av en rot
- Rot ur en rot
- Rationalisering
En rot är ett uttryck av formen  , där
, där  och
och  . Om
. Om  dessutom är ett jämnt tal, kan
dessutom är ett jämnt tal, kan  inte vara negativt
inte vara negativt  .
.
Talet  är till exempel ett jämnt tal. Därför är
är till exempel ett jämnt tal. Därför är 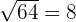 ; medan
; medan  .
.
Och eftersom talet  är udda, är
är udda, är  och
och 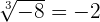 . Det betyder att kubikroten är definierad för varje reellt tal.
. Det betyder att kubikroten är definierad för varje reellt tal.

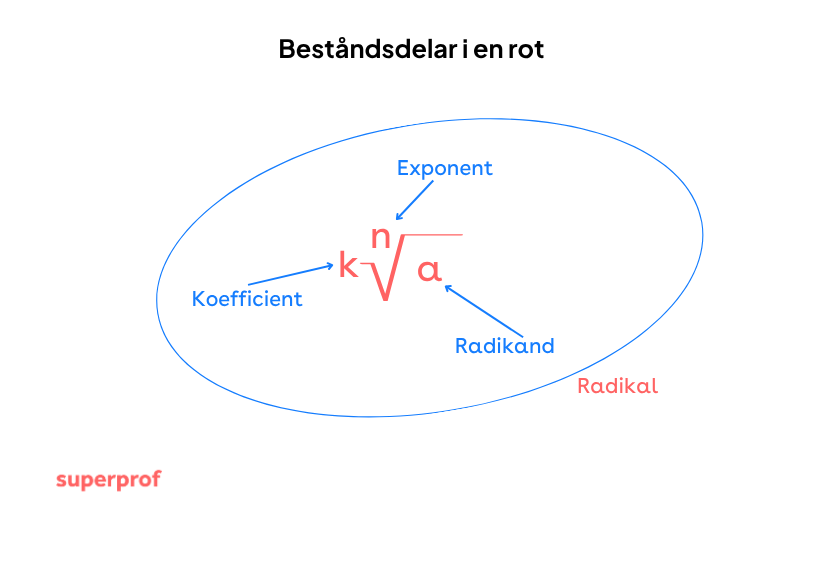
Beståndsdelar i en rot
Potenser och rötter
En rot kan uttryckas som en potens:
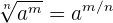
Exempel:
Vi skriver talet  som en potens:
som en potens: 
Rotexponenten för roten  blir nämnare och exponenten för radikanden
blir nämnare och exponenten för radikanden 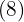 blir täljare. Vi beräknar:
blir täljare. Vi beräknar:
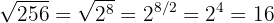
Lika rötter
Med användning av exponentskrivningen för bråk och egenskapen hos bråk, som säger att bråket är ekvivalent om täljare och nämnare multipliceras med samma tal, gäller:
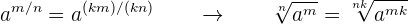
Multiplicerar eller dividerar man rotexponenten och exponenten/exponenterna för radikanden med samma naturliga tal, så erhåller man en annan lika rot.
Beispiel
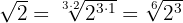
Förenkling av rötter
Om det finns ett naturligt tal som rotexponenten och exponenten (eller exponenterna) för radikanden kan divideras med, erhåller man en förenklad rot.
Exempel:
1 Förenkla 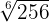
Vi skriver  som en potens:
som en potens: 
För att förenkla roten dividerar vi både rotexponenten  och exponenten för radikanden
och exponenten för radikanden 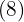 med
med 
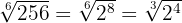
2 Förenkla 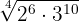
För att förenkla roten dividerar vi både rotexponenten  och exponenterna för radikanden
och exponenterna för radikanden 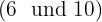 med
med 
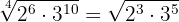
Gemensam rotexponent
För att få två eller flera rötter på en gemensam rotexponent, krävs följande steg:
1 Vi bestämmer den minsta gemensamma multipeln, som sedan är den gemensamma rotexponenten
2 Vi dividerar den minsta gemensamma multipeln med var och en av rotexponenterna och multiplicerar varje resultat med motsvarande exponenter
Exempel:
Vi bestämmer den gemensamma rotexponenten:

Först bestämmer vi mgm för rotexponenterna: 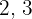 und
und 
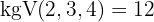
Vi dividerar den gemensamma rotexponenten  med var och en av rotexponenterna
med var och en av rotexponenterna 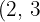 och
och 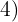 och multiplicerar varje resultat med motsvarande exponenter
och multiplicerar varje resultat med motsvarande exponenter

Vi räknar med potenserna

Delvis rotutdragning
För att extrahera faktorer ur en rot, faktoriseras radikanden. Om:
En exponent för radikanden är mindre än rotexponenten
Motsvarande faktor stannar kvar under radikanden.
Exempel:
1 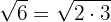
2 
En exponent för radikanden är lika med rotexponenten
Motsvarande faktor lämnar radikanden.
Exempel:
1 
Vi faktoriserar talet  . Eftersom
. Eftersom  upphöjs till samma potens som rotexponenten, kan vi extrahera
upphöjs till samma potens som rotexponenten, kan vi extrahera  ur radikanden
ur radikanden
2 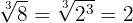
Vi faktoriserar talet  . Eftersom
. Eftersom  upphöjs till samma potens som rotexponenten, kan vi extrahera
upphöjs till samma potens som rotexponenten, kan vi extrahera  ur radikanden
ur radikanden
En exponent för radikanden är större än rotexponenten
Denna exponent divideras med rotexponenten. Den erhållna kvoten är exponenten för faktorn utanför radikanden och resten är exponenten för faktorn inuti radikanden
Exempel:
1 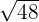
Exponenten för 2 är större än rotexponenten. Denna exponent  divideras alltså med rotexponenten
divideras alltså med rotexponenten 
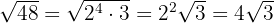
Den erhållna kvoten  är exponenten för faktorn utanför radikanden och resten
är exponenten för faktorn utanför radikanden och resten 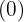 är exponenten för faktorn inuti radikanden.
är exponenten för faktorn inuti radikanden.
Eftersom faktorn  är lika med 1, behöver den inte tas in i radikanden, eftersom den inte ändras när den multipliceras med en annan faktor.
är lika med 1, behöver den inte tas in i radikanden, eftersom den inte ändras när den multipliceras med en annan faktor.
I allmänhet gäller: Om resultatet av divisionen av exponenten för en faktor med rotexponenten ger noll, tas denna faktor inte in i radikanden
2 
Vi faktoriserar: 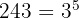
Exponenten är större än rotexponenten. Alltså divideras denna exponent  med rotexponenten
med rotexponenten 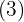 .
.
Den erhållna kvoten  är exponenten för faktorn utanför radikanden och resten
är exponenten för faktorn utanför radikanden och resten  är exponenten inuti radikanden.
är exponenten inuti radikanden.

3 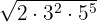
Det finns exponenter i radikanden som är större än rotexponenten. Alltså divideras dessa exponenter 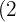 och
och 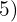 med rotexponenten
med rotexponenten  .
.
Var och en av de erhållna kvoterna  och
och  är då exponenten för motsvarande faktor utanför radikanden och de erhållna resterna
är då exponenten för motsvarande faktor utanför radikanden och de erhållna resterna  och
och  är då exponenterna för motsvarande faktorer inuti radikanden.
är då exponenterna för motsvarande faktorer inuti radikanden.

4 
Exponenterna för radikanden är större än rotexponenten. Alltså divideras dessa exponenter  och
och 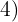 med rotexponenten
med rotexponenten  .
.
Var och en av kvoterna 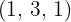 är då motsvarande faktor utanför radikanden och de erhållna resterna
är då motsvarande faktor utanför radikanden och de erhållna resterna 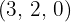 är då exponenterna för motsvarande faktorer inuti radikanden
är då exponenterna för motsvarande faktorer inuti radikanden
Att ta in faktorer under roten
För att ta in faktorer under en rot, måste faktorerna upphöjas till rotens rotexponent
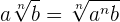
Exempel:
1 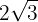
Eftersom rotexponenten är  , kvadreras faktorn utanför roten
, kvadreras faktorn utanför roten  och vi beräknar
och vi beräknar
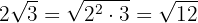
2 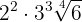
Både  och
och  upphöjs till fyra:
upphöjs till fyra:
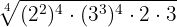
Vi löser upp parenteserna genom att multiplicera exponenterna

Vi multiplicerar potenserna med samma bas
Addition och subtraktion av rötter
Två rötter kan endast adderas (eller subtraheras) om rötterna är lika. Det betyder att det måste röra sig om rötter som har samma rotexponent och radikand.
För att addera/subtrahera rötter med samma rotexponent och radikand, adderas/subtraheras koefficienterna för rötterna.

Exempel:
1 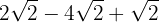
Vi sammanfattar koefficienterna för rötterna
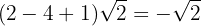
2 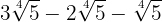
Vi slår samman koefficienterna för rötterna
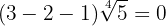
3 
Vi faktoriserar radikanderna:

Rötterna är alltså
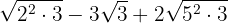
Vi extraherar faktorerna ur rötterna och multiplicerar dem med koefficienten för motsvarande rot
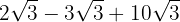
Vi slår samman koefficienterna för rötterna
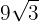
4 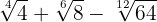
Vi extraherar faktorerna ur rötterna och multiplicerar dem med koefficienten för motsvarande rot
Alltså
Vi förenklar rötterna. För den första roten dividerar vi rotexponenten och exponenten för radikanden med  , för den andra roten med
, för den andra roten med  och för den tredje roten med
och för den tredje roten med 
Vi slår samman koefficienterna för rötterna
Exempeluppgifter om addition och subtraktion av rötter
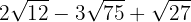
Multiplikation av rötter med samma rotexponent
För att multiplicera rötter med samma rotexponent, multipliceras radikanderna och rotexponenten förblir densamma.
Exempel:
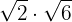
Så snart vi har utfört ett räknesteg, extraherar vi, om möjligt, faktorer ur roten.
Multiplikation av rötter med olika rotexponenter
Först måste de tas på en gemensam rotexponent, därefter multipliceras de.
Exempel:
1
Vi faktoriserar radikanderna
Vi tar på gemensam rotexponent och måste alltså beräkna den minsta gemensamma multipeln för rotexponenterna. Detta är då den gemensamma rotexponenten.
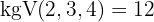
Vi dividerar den gemensamma rotexponenten  med var och en av rotexponenterna och varje erhållet resultat multiplicerar vi med motsvarande exponenter . Vi utför produkten av potenserna med samma bas i radikanden och extraherar faktorer ur radikanden
med var och en av rotexponenterna och varje erhållet resultat multiplicerar vi med motsvarande exponenter . Vi utför produkten av potenserna med samma bas i radikanden och extraherar faktorer ur radikanden
2
Vi beräknar den minsta gemensamma multipeln för rotexponenterna
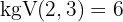
Vi dividerar den gemensamma rotexponenten  med var och en av rotexponenterna och upphöjer varje resultat till motsvarande radikand
med var och en av rotexponenterna och upphöjer varje resultat till motsvarande radikand
Vi faktoriserar  och
och  , utför de nödvändiga räknestegen och extraherar faktorer
, utför de nödvändiga räknestegen och extraherar faktorer
Division av rötter med samma rotexponent
För att dividera rötter med samma rotexponent, divideras radikanderna och rotexponenten förblir densamma.
Exempel:
Eftersom rötterna har samma rotexponent, kan vi skriva allt under en rot
Vi faktoriserar och dividerar potenserna med samma bas
Vi förenklar roten genom att dividera rotexponenten och radikanden med 
Division av rötter med olika rotexponenter
Först tar vi på en gemensam rotexponent, därefter dividerar vi.
Exempel:
1
Först tar vi på en gemensam rotexponent. Alltså måste vi beräkna den minsta gemensamma multipeln för rotexponenterna, som sedan är den gemensamma rotexponenten. .
Vi dividerar den gemensamma rotexponenten  med var och en av rotexponenterna (
med var och en av rotexponenterna ( och
och  ) och multiplicerar varje resultat med motsvarande exponenter (
) och multiplicerar varje resultat med motsvarande exponenter ( och
och  )
)
Vi faktoriserar  för att kunna utföra divisionen på följande sätt
för att kunna utföra divisionen på följande sätt
2
Vi utför samma steg som i föregående exempel
Vi förenklar roten genom att dividera rotexponenten och exponenten för radikanden med  och extraherar slutligen faktorer
och extraherar slutligen faktorer
Potens av en rot
För att upphöja en rot till en exponent, upphöjs radikanden till exponenten. Rotexponenten förblir densamma.
Exempel:
1
Vi kvadrerar radikanden, faktoriserar  och kvadrerar. Och slutligen skriver vi faktorn framför roten
och kvadrerar. Och slutligen skriver vi faktorn framför roten
2
Vi upphöjer radikanderna till fyra, faktoriserar dem och extraherar  ur roten
ur roten
Vi utför de nödvändiga räknestegen för att räkna med potenser i radikanderna och bestämmer den gemensamma rotexponenten för att kunna dividera
Vi förenklar roten genom att dividera rotexponenten och exponenterna för radikanden med  och utför en division av potenser med samma exponent
och utför en division av potenser med samma exponent
3 Skriv följande potenser som rötter:
4 Skriv som potens med rationell exponent
Rot ur en rot
Roten ur en rot är en annan rot med samma radikand, vars rotexponent är produkten av de båda rotexponenterna.
Exempel:
1
Vi multiplicerar rotexponenterna
2
Vi tar in den första  under kubikroten. För detta måste vi upphöja den till tre och multiplicera potenserna med samma bas
under kubikroten. För detta måste vi upphöja den till tre och multiplicera potenserna med samma bas
Vi tar in under den fjärde roten. Alltså måste vi upphöja den till fyra, multiplicera potenserna och slutligen multiplicera rotexponenterna
Rationalisering
Vid rationalisering av en rot måste rötterna elimineras från nämnaren. Detta underlättar till exempel addition av bråk
Det finns tre olika fall:
Fall 1
Rationalisering av typen 
Zähler und Nenner werden mit multipliziert
Exempel:
Fall 2
Rationalisering av typen
Täljare och nämnare multipliceras med multipliziert
Exempel:
Vi skriver radikanden  som en potens:
som en potens:
Vi måste multiplicera täljaren och nämnaren med den femte roten ur
Vi multiplicerar rötterna i nämnaren, extraherar faktorer ur roten och förenklar bråket
Fall 3
Rationalisering av typen
Och i allmänhet, när nämnaren är ett binom med åtminstone en rot.
Bråket förlängs med det konjugerade uttrycket som står i nämnaren.
Det konjugerade binomet är alltid lika med binomet med omvänt tecken:
Dessutom måste vi tänka på: "Summa gånger differens är lika med kvadratdifferens".
Exempel:
1
Vi multiplicerar täljaren och nämnaren med det konjugerade till nämnaren, löser upp parentesen i täljaren och räknar summa gånger differens i nämnaren. Så får vi en kvadratdifferens
2
Vi förlänger bråket med det konjugerade till nämnaren
3
Vi multiplicerar täljaren och nämnaren med det konjugerade till nämnaren, löser upp parentesen i täljaren och räknar summa gånger differens i nämnaren. Så får vi en kvadratdifferens
Sammanfatta med AI:












