Lös följande sannolikhetsuppgifter:
Hur stor är sannolikheten att följande resultat uppstår när man kastar två mynt:
A Två krona
B Två klave
C En krona och en klave
Hur stor är sannolikheten att följande resultat uppstår när man kastar två mynt:
A Två krona.
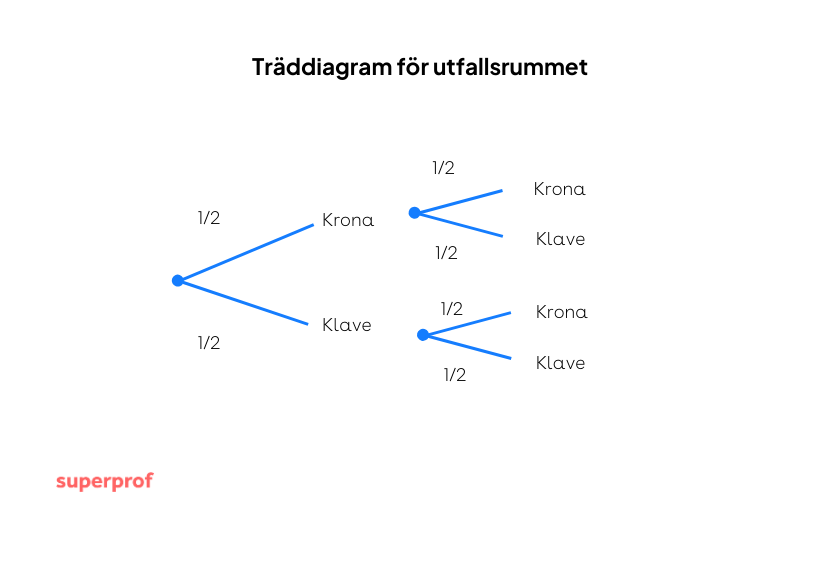
Eftersom två händelser kan inträffa och de är oberoende av varandra, multiplicerar man sannolikheten att myntet visar "krona" (1/2) med sannolikheten att myntet visar "klave" (också 1/2).
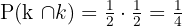
B Två klave.
Sannolikheten att myntet visar klave eller krona är båda 1/2, som visas i schemat. Eftersom båda händelserna är oberoende multiplicerar man sannolikheterna:
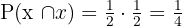
C En krona och en klave.
Sannolikheten att få en krona och en klave kan inträffa i två olika scenarier: 1. första kastet krona och andra kastet klave, 2. första kastet klave och andra krona. Man beräknar först sannolikheten för varje scenario (1/2 * 1/2) och summerar sedan dem:
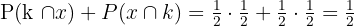
Hur stor är sannolikheten att man vid ett klassiskt dominospel, när man drar en dominobricka, får en poängsumma som är större än 9 eller ett multipel av 4?
Hur stor är sannolikheten att man vid ett klassiskt dominospel, när man drar en dominobricka, får en poängsumma som är större än 9 eller ett multipel av 4?
Samla under A alla dominobrickor vars totala poängsumma är högre än 9. Under B listar vi alla dominobrickor vars poängsummer är ett multipel av 4:
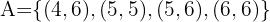
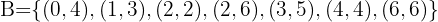
Vi ser att dominobrickan (6,6) tillhör båda grupperna, alltså 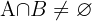 .
.
Därför använder vi formeln 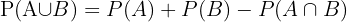 för att få den efterfrågade sannolikheten.
för att få den efterfrågade sannolikheten.
Eftersom det totalt finns 28 dominobrickor, blir sannolikheten:
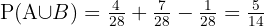
En tärning är konstruerad så att sannolikheten för varje tärningssida är proportionell mot dess ögonantal. Hur sannolikt är det vid första kastet att:
A få en 6:a
B få ett udda tal
En tärning är konstruerad så att sannolikheten för varje tärningssida är proportionell mot dess ögonantal. Hur sannolikt är det vid första kastet att:
A få en 6:a?
Sannolikheten för varje ögonantal är proportionell mot numret på tärningen. Om vi låter proportionalitetsfaktorn vara p, får vi:
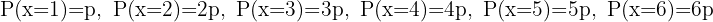
Summan av alla sannolikheter måste vara 1:
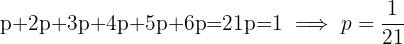
Därmed blir sannolikheten för att få en 6:a:
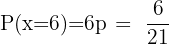
B få ett udda tal?
Sannolikheten för ett udda tal är summan av sannolikheterna för 1, 3 och 5:
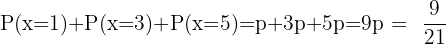
När två tärningar kastas, noteras summan av tärningarna. Beräkna:
A Hur stor är sannolikheten att summan blir 7?
B Hur stor är sannolikheten att summan blir jämn?
C Hur stor är sannolikheten att summan blir ett multipel av 3?
När man kastar två tärningar och summerar ögonantalet på tärningarna:
A Sannolikheten att summan blir 7:
De möjliga kombinationerna som ger summan 7 är:

Totalt 6 möjliga kombinationer. Eftersom det finns 36 möjliga utfall totalt, är sannolikheten:
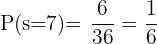
B Sannolikheten att summan är jämn:
Ögonpar som ger en jämn summa är:
-
- (1,1)
- (1,3),(2,2),(3,1)
- (1,5),(2,4),(3,3),(4,2),(5,1)
- (2,6),(3,5),(4,4),(5,3),(6,2)
- (4,6),(5,5),(6,4)
- (6,6)
Totalt 18 möjligheter, så sannolikheten är:
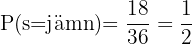
C Sannolikheten att summan är ett multipel av 3:
De summor som är multipler av 3 visas i följande bild:
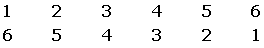
Totalt 12 möjligheter, alltså är sannolikheten:
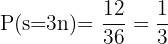
Tre tärningar kastas. Hur stor är sannolikheten att:
A Alla tärningar visar 6?
B Summan av tärningarna blir 7?
Tre tärningar kastas. Hur stor är sannolikheten att:
A Alla tärningar visar 6?
Det finns bara ett sätt att få tre sexor (6,6,6) och med tanke på att det finns 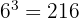 möjliga utfall, är den sökta sannolikheten
möjliga utfall, är den sökta sannolikheten 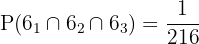
B Summan av tärningarna blir 7?
De olika tärningskombinationerna som ger summan 7 är följande:

Det finns alltså 15 sätt att få summan 7, vilket innebär att den sökta sannolikheten är:
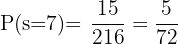
Hur stor är sannolikheten att man vid ett tärningskast får:
A ett jämnt tal?
B ett tal som är en multipel av tre?
C ett tal som är större än 4?
Hur stor är sannolikheten att man vid ett tärningskast får:
A ett jämnt tal?
Av de 6 möjliga utfallen finns det 3 jämna tal. Sannolikheten blir därför
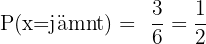
B ett tal som är en multipel av tre?
Multiplar av tre är: 3 och 6. Det finns alltså två möjligheter att få en multipel av 3. Sannolikheten är
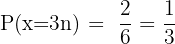
C ett tal som är större än 4?
De utfall som är större än 4 är 5 och 6. Sannolikheten blir därför
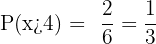
Vid ett lotteri dras två kulor från en trumma som totalt innehåller fyra kulor: en vit (V), en röd (R), en grön (G) och en svart (S). Beskriv utfallsrummet för fallet när:
A den första kulan läggs tillbaka i trumman innan den andra dras.
B den första kulan inte läggs tillbaka i trumman.
Vid ett lotteri dras två kulor från en trumma som totalt innehåller fyra kulor: en vit, en röd, en grön och en svart. Beskriv utfallsrummet för fallet när:
A den första kulan läggs tillbaka i trumman innan den andra dras.
Den första kulan kan vara vilken som helst av de fyra kulorna V, R, G, S. När den första kulan har dragits och lagts tillbaka i trumman kan vilken som helst av de fyra kulorna dras igen. Till exempel, om den vita kulan (V) drogs först, kan resultatet av det andra draget bli VV, VR, VG eller VS. På samma sätt för alla andra alternativ. Vårt utfallsrum blir därför:
E = {VV, VR, VG, VS, RV, RR, RG, RS, GV, GR, GG, GS, SV, SR, SG, SS}
B den första kulan inte läggs tillbaka i trumman.
Eftersom kulan som drogs först inte läggs tillbaka i trumman för det andra draget, blir utfallsrummet:
E = {VR, VG, VS, RV, RG, RS, GV, GR, GS, SV, SR, SG}
En lottrumma innehåller 8 röda, 5 gula och 7 gröna kulor. Hur stor är sannolikheten att vid det första draget kulan är:
A röd
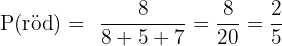
B grön
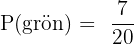
C gul
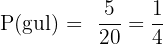
D inte röd
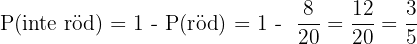
E inte gul
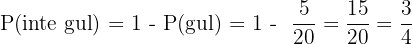
En lottrumma innehåller 8 röda, 5 gula och 7 gröna kulor. Hur stor är sannolikheten att vid det första draget kulan är:
A röd:
Av totalt 20 kulor är 8 röda. Sannolikheten är alltså:
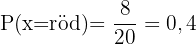
B grön:
Eftersom det finns 7 gröna kulor blir sannolikheten:
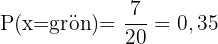
C gul:
5 av 20 kulor är gula, så sannolikheten är:
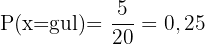
D inte röd:
Sannolikheten att inte dra en röd kula är:
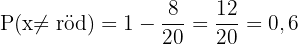
E inte gul:
Samma logik som ovan:
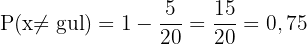
En lottrumma innehåller tre röda och 7 vita kulor. Två valfria kulor dras. Beskriv utfallsrummet och sannolikheten för fallet:
A två kulor dras, där varje kula återlämnas till lottrumman innan nästa dragning.
Eftersom varje kula återlämnas efter dragning kan varje dragning ge någon av de 10 kulorna (3 röda, 7 vita). Utfallsrummet blir:
E = {RR, RV, VR, VV}
B två kulor dras utan att återlämnas.
Nu påverkar den första dragningen den andra. Utfallsrummet blir:
E = {RR, RV, VR, VV}
En lottrumma innehåller tre röda och sju vita kulor. Två kulor dras. Beskriv utfallsrummet och sannolikheten för fallet:
A två kulor dras, där varje kula återlämnas till lottrumman efter dragning.
Utfallsrummet blir:
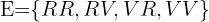
Sannolikheterna är:
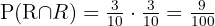
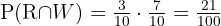
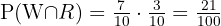
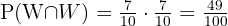
B två kulor dras utan att återlämnas.
Utfallsrummet blir:
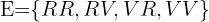
Sannolikheterna är:
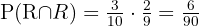
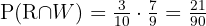
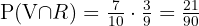
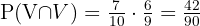
En kula dras från en lottrumma med 4 röda, 5 vita och 6 svarta kulor.
A Hur stor är sannolikheten att kulan är röd eller vit?
B Hur stor är sannolikheten att kulan inte är vit?
En kula dras från en lottrumma med 4 röda, 5 vita och 6 svarta kulor.
A Hur stor är sannolikheten att kulan är röd eller vit?
B Hur stor är sannolikheten att kulan inte är vit?
För dessa händelser finns inga beroende element, dvs. från formeln
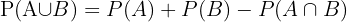
kvarstår endast
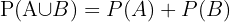
Så sannolikheten att kulan är röd eller vit blir:
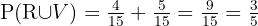
Och sannolikheten att kulan INTE är vit:
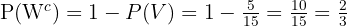
I en skolklass finns 10 blonda och 20 brunhåriga tjejer, samt fem blonda och 10 brunhåriga killar. På en skoldag deltar endast 44 elever i undervisningen. Hur stor är sannolikheten att den frånvarande eleven är:
A manlig
B kvinnlig och brunett
C manlig eller kvinnlig
I en skolklass finns 10 blonda och 20 brunhåriga tjejer, samt fem blonda och 10 brunhåriga killar. På en skoldag deltar endast 44 elever i undervisningen.
A manlig
I följande tabell har vi sammanställt all information överskådligt:
[table “366” could not be loaded /]
Det går att se att det finns 15 killar och totalt 45 elever. Sannolikheten att den frånvarande eleven är manlig är därför
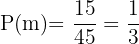
B kvinnlig och brunett
Det finns 20 brunhåriga tjejer, alltså
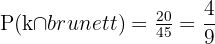
I detta fall är sannolikheten den totala summan, alltså
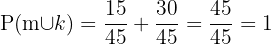
Ett kuvert innehåller 20 lappar. På åtta av dem finns en bil avbildad, resten är vita. Hur stor är sannolikheten att vid ett drag få åtminstone en lapp med en bil avbildad?
A om man drar en lapp?
B om man drar två lappar?
C om man drar tre lappar?
Ett kuvert innehåller 20 lappar. På åtta av dem finns en bil (A) avbildad, resten är vita (W). Hur stor är sannolikheten att vid ett drag få åtminstone en lapp med en bil avbildad?
A Om man drar en lapp?
Eftersom det finns 8 lappar med bil och totalt 20 lappar, är sannolikheten att dra en lapp med bil 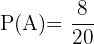
B Om man drar två lappar?
När man drar två lappar kan resultaten vara WW, AW, WA eller AA. Det enklaste är att först beräkna sannolikheten för WW och sedan subtrahera från 1:
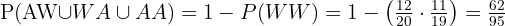
C Om man drar tre lappar?
Samma logik som ovan tillämpas: 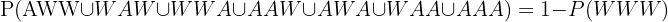
Därför är
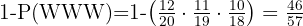
Eleverna A och B har sannolikheterna 1/2 respektive 1/5 att inte klara ett prov. Sannolikheten att båda två inte klarar provet är 1/10. Bestäm sannolikheten att minst en av de två eleverna inte klarar provet.
Eleverna A och B har sannolikheterna 1/2 respektive 1/5 att inte klara ett prov. Sannolikheten att båda inte klarar provet är 1/10. Bestäm sannolikheten att minst en av de två eleverna inte klarar provet.
Eftersom de två händelserna är beroende av varandra, är sannolikheten inte noll. Sannolikheten beräknas på följande sätt:
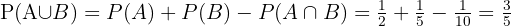
Två bröder går på hobbyskytte. Den första träffar målet i genomsnitt vid två av fem skott, den andra vid ett av två skott. Om båda skjuter på samma mål samtidigt, med vilken sannolikhet träffar de målet?
Två bröder går på hobbyskytte. Den första träffar målet i genomsnitt vid två av fem skott, den andra vid ett av två skott. Om båda skjuter på samma mål samtidigt, med vilken sannolikhet träffar de målet?
Sannolikheten att den första brodern träffar målet är:
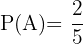
Sannolikheten att den andra brodern träffar målet är:
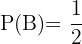
Sannolikheten att båda bröderna träffar målet samtidigt är:
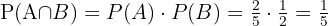
Det vill säga, sannolikheten att antingen broder A eller broder B träffar målet när de skjuter samtidigt är:
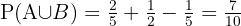
I en klass finns 10 män och 20 kvinnor. Hälften av männen och hälften av kvinnorna har bruna ögon. Hur sannolikt är det att en slumpmässigt vald person är en man med bruna ögon?
I en klass finns 10 män och 20 kvinnor. Hälften av männen och hälften av kvinnorna har bruna ögon. Hur sannolikt är det att en slumpmässigt vald person är en man med bruna ögon?
[table “57” could not be loaded /]
Här måste man skilja på att det totalt finns 10 män, totalt 15 personer med bruna ögon och totalt 5 män med bruna ögon, för att beräkna sannolikheten:
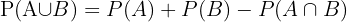
Vi beräknar
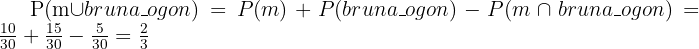
Sannolikheten att en man blir 20 år är 1/4. Sannolikheten att hans fru blir 20 år är 1/3. Hur hög är sannolikheten att:
A båda personerna blir 20 år?
B mannen blir 20 år men frun inte.
C båda dör innan de fyller 21?
Sannolikheten att en man blir 20 år är 1/4. Sannolikheten att hans fru blir 20 år är 1/3. Hur hög är sannolikheten att:
A båda personerna blir 20 år?
Händelserna är oberoende av varandra, eftersom den ena personens livslängd inte påverkar den andra. Sannolikheten kan därför beräknas så här:
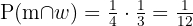
B mannen blir 20 år men frun inte.
Återigen oberoende händelser. Här används komplementet för frun:
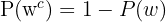
Alltså:
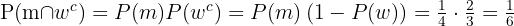
C båda dör innan de fyller 21?
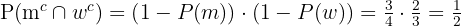
Beräkna sannolikheten att få exakt två klave när man kastar ett mynt fyra gånger.
Beräkna sannolikheten att få exakt två klave när man kastar ett mynt fyra gånger.
Möjliga utfall vid ett myntkast är krona (K) eller klave (Z).
Först bestämmer vi på vilka sätt man kan få exakt två klave (Z) vid fyra kast.
Vi bestämmer på hur många sätt man av fyra möjliga utfall (n=4) kan få två lika (r=2). Det vill säga, vi beräknar antalet kombinationer av fyra utfall som består av två lika element.
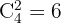
Vi får alltså 6 utfall. Illustrerat är de 6 möjliga utfallen:
ZZKK, ZKZK, ZKKZ, KZZK, KZKZ, KKZZ
Totala antalet möjliga utfall när man kastar myntet fyra gånger är: 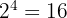
Sannolikheten att få exakt två klave vid fyra kast är alltså:
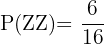
En grupp på 10 personer sätter sig på en bänk. Hur stor är sannolikheten att två personer som tidigare valts slumpmässigt (utan deras vetskap) sätter sig bredvid varandra?
En grupp på 10 personer sätter sig på en bänk. Hur stor är sannolikheten att två personer som tidigare valts slumpmässigt (utan deras vetskap) sätter sig bredvid varandra?
För att ta reda på hur många olika sätt 10 personer kan sätta sig på 10 platser använder vi permutationerna
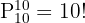
För att nu bestämma på hur många sätt två förutvalda personer kan sitta bredvid varandra, måste man tänka på att de två personerna kan inta en av 9 möjliga platser om de sitter tillsammans: antalet sätt som 9 personer kan sätta sig på 9 platser är:
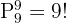
Eftersom de två personerna kan sitta tillsammans på två sätt (AB eller BA), är det totala antalet möjliga sätt för två förutvalda personer på 10 platser lika med 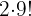 , vilket ger sannolikheten att detta händer:
, vilket ger sannolikheten att detta händer:
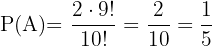
5 kort dras från en kortlek med totalt 52 kort. Hur stor är sannolikheten att
A dra 4 ess?
B dra 4 ess och en kung?
C dra 3 femmor och 2 knektar?
D dra 9, 10, knekt, dam och kung i ordning?
E dra 3 kort av en färg och 2 av en annan?
F dra minst 1 ess?
5 kort dras från en kortlek med totalt 52 kort. Hur stor är sannolikheten att
A dra 4 ess?
Det totala antalet sätt att dra 5 kort från 52 är
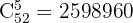
Antalet sätt att välja 4 ess är 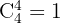 och för det femte kortet kan vilket som helst av de återstående 48 korten dras
och för det femte kortet kan vilket som helst av de återstående 48 korten dras 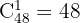
Sannolikheten blir därför
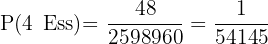
B dra 4 ess och en kung?
Det finns 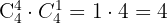 sätt att dra 4 ess och en kung.
sätt att dra 4 ess och en kung.
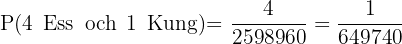
C dra 3 femmor och 2 knektar?
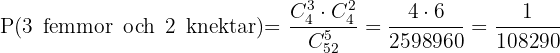
D dra 9, 10, knekt, dam och kung i ordning?
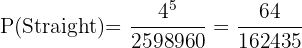
E dra 3 kort av en färg och 2 av en annan?
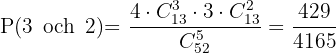
F dra minst 1 ess?
Först beräknar man sannolikheten att inte dra något ess:
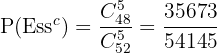
Sannolikheten att dra minst ett ess blir:
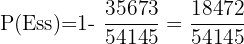
Sammanfatta med AI:


