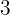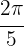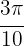I den här artikeln hittar du en rad uppgifter som ska lösas med hjälp av trigonometri. Under lösningarna till varje uppgift beskrivs alla beräkningar steg för steg.
Omvandla radianmått till gradmått
Formeln för att omvandla en vinkel från radianmått till gradmått är följande:
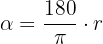
Där  är vinkeln i radianer. I grader blir vinklarna alltså:
är vinkeln i radianer. I grader blir vinklarna alltså:
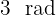 Här är
Här är 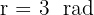 .
.
Gradmåttet blir då: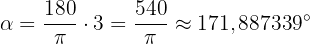
För att få vinkeln i grader, minuter och sekunder gör vi följande:
Multiplicera decimaldelen med 60 för minuter: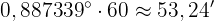
Multiplicera decimaldelen av minuter med 60 för sekunder: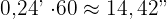
Därför är vinkeln i grader, minuter och sekunder: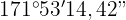
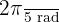 Vi använder samma formel:
Vi använder samma formel: 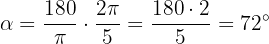
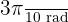 Samma procedur:
Samma procedur: 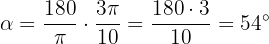
Ange följande vinklar i radianer:
Formeln för att omvandla grader till radianer är mycket lik den tidigare:
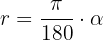
Vinklarna blir:
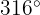 Använd formeln:
Använd formeln: 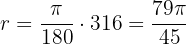 Vinkeln i radianer är alltså
Vinkeln i radianer är alltså 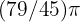 .
.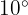 Använd formeln:
Använd formeln: 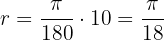 Vinkeln i radianer är alltså
Vinkeln i radianer är alltså 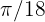 .
. Använd formeln:
Använd formeln:  Här kan inget förenklas eftersom 127 är ett primtal. Vinkeln i radianer är alltså
Här kan inget förenklas eftersom 127 är ett primtal. Vinkeln i radianer är alltså 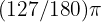 .
.
Givet är 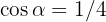 och
och  270^{\circ} < \alpha < 360^{\circ}[/latex]. Beräkna de övriga trigonometriska funktionerna för vinkeln [latex]\alpha[/latex].
270^{\circ} < \alpha < 360^{\circ}[/latex]. Beräkna de övriga trigonometriska funktionerna för vinkeln [latex]\alpha[/latex].
Vi vet att vinkeln ligger i fjärde kvadranten i koordinatsystemet. För denna kvadrant gäller 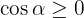 , men
, men 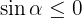 . Därför får vi:
. Därför får vi:
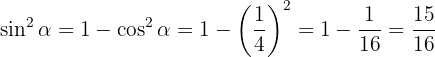
Därmed får vi:
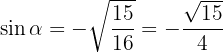
Eftersom vi nu har 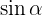 och
och  , är det enkelt att bestämma de andra trigonometriska funktionerna:
, är det enkelt att bestämma de andra trigonometriska funktionerna:
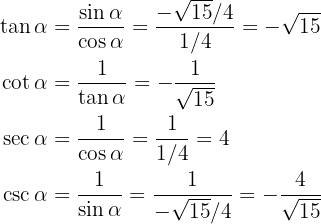
Man kan också rationalisera nämnaren för kotangens och kosekans. Då blir resultaten lika korrekta:
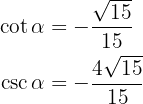
Dessa resultat fås genom att multiplicera de tidigare uttrycken med 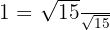 . På så sätt undviker vi att ha kvadratrötter i nämnaren.
. På så sätt undviker vi att ha kvadratrötter i nämnaren.
Givet är 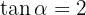 och
och  180^{\circ} < \alpha < 270^{\circ}[/latex]. Beräkna de övriga trigonometriska funktionerna för vinkeln [latex]\alpha[/latex].
180^{\circ} < \alpha < 270^{\circ}[/latex]. Beräkna de övriga trigonometriska funktionerna för vinkeln [latex]\alpha[/latex].
Vinkeln  ligger i tredje kvadranten i koordinatsystemet.
ligger i tredje kvadranten i koordinatsystemet.
Därför vet vi att
 och
och 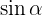 .
.
Relationen mellan tangens och sekans kan också beräknas med hjälp av Pythagoras sats:
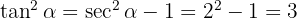
Därmed får vi:
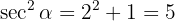
Eftersom  , gäller
, gäller 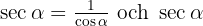 .
.
Alltså:
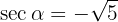
Därifrån får vi:
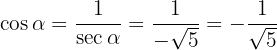
Man kan också skriva 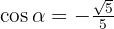 om man rationaliserar nämnaren.
om man rationaliserar nämnaren.
Vi vet även att 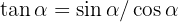 . Därmed får vi:
. Därmed får vi:
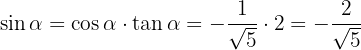
De övriga två trigonometriska funktionerna kan nu enkelt beräknas:
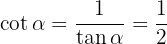
och
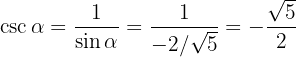
Givet är 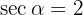 och
och  0 < \alpha < \pi / 2[/latex]. Beräkna de övriga trigonometriska funktionerna för vinkeln [latex]\alpha[/latex].
0 < \alpha < \pi / 2[/latex]. Beräkna de övriga trigonometriska funktionerna för vinkeln [latex]\alpha[/latex].
Vinkeln är given i radianer. Dessutom ligger den i första kvadranten i koordinatsystemet, därför gäller 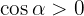 och
och 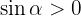 .
.
Relationen mellan sekans och 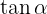 kan beräknas med Pythagoras sats:
kan beräknas med Pythagoras sats:
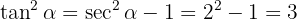
Eftersom 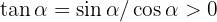 , och både
, och både 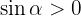 och
och 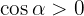 , får vi:
, får vi:
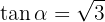
Likaså är:
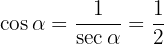
Då 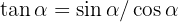 , får vi:
, får vi:
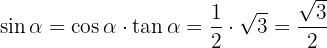
De övriga trigonometriska funktionerna kan nu enkelt bestämmas:
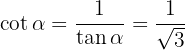
och
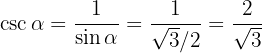
Beräkna sinus, cosinus och tangens för följande vinklar:
Vi antar att sinus och cosinus för de mest kända vinklarna (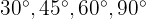 , etc.) redan är kända:
, etc.) redan är kända:
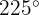 För att beräkna sinus använder vi egenskaperna hos förskjutning av sinus- och cosinusfunktionerna.
För att beräkna sinus använder vi egenskaperna hos förskjutning av sinus- och cosinusfunktionerna.
Vi kan se att: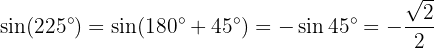
På samma sätt: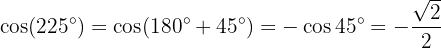
Slutligen: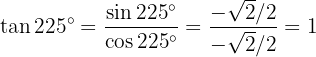
 På samma sätt använder vi egenskaperna för förskjutning av sinus- och cosinusfunktioner.
På samma sätt använder vi egenskaperna för förskjutning av sinus- och cosinusfunktioner.
Vi får: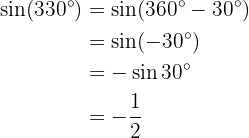
På samma sätt: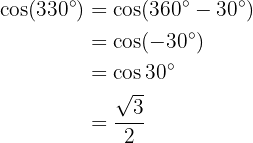
Slutligen: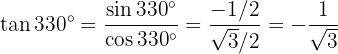
Bestäm de trigonometriska funktionerna för följande vinklar:
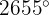 Först behöver vi hitta en vinkel mellan
Först behöver vi hitta en vinkel mellan  och
och 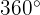 som är ekvivalent med
som är ekvivalent med 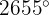 . Vi delar 2655 med 360 och tar resten:
. Vi delar 2655 med 360 och tar resten: 
Resten är 135, så vi får: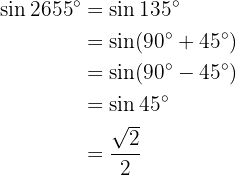
På samma sätt: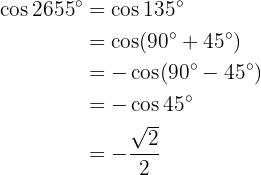
Slutligen: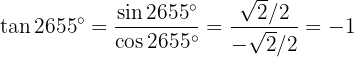
 Här gör vi på samma sätt: vi delar först 840 med 360 och använder resten:
Här gör vi på samma sätt: vi delar först 840 med 360 och använder resten: 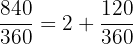
Så är ekvivalent med
är ekvivalent med 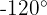 .
.
Därmed: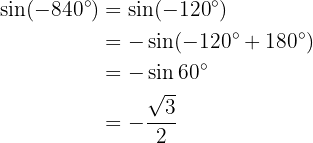
På samma sätt: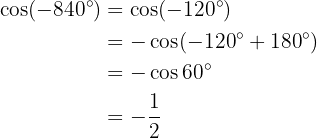
Slutligen: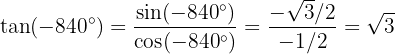
Givet är den rätvinkliga triangeln ABC med den räta vinkeln vid  . Vi vet att
. Vi vet att  och att vinkeln
och att vinkeln 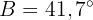 . Beräkna de två andra vinklarna och sidlängderna.
. Beräkna de två andra vinklarna och sidlängderna.
Titta på skissen av triangeln:
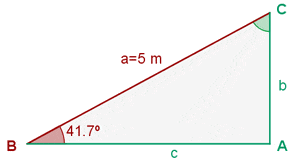
Här kan du se de saknade måtten (sidorna  ,
,  och vinkeln
och vinkeln  ). Det enklaste är att först beräkna vinkeln
). Det enklaste är att först beräkna vinkeln  , eftersom summan av vinklarna i en triangel alltid är
, eftersom summan av vinklarna i en triangel alltid är  . Därför är
. Därför är
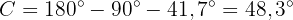
Eftersom triangeln är rätvinklig kan vi använda trigonometriska funktioner för att bestämma längderna på de övriga sidorna. Vi vet att
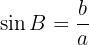
Därför är
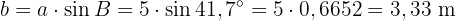
Eftersom 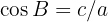 gäller också
gäller också
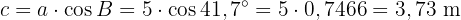
På så sätt har vi nu beräknat alla saknade mått.
Givet är den rätvinkliga triangeln ABC med den räta vinkeln vid  . Vi vet att
. Vi vet att 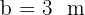 och att vinkeln
och att vinkeln 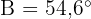 . Beräkna de två andra vinklarna och sidlängderna.
. Beräkna de två andra vinklarna och sidlängderna.
Titta på skissen av triangeln:
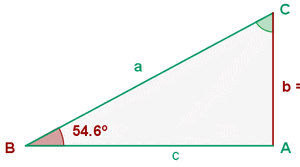
Här kan du se de saknade uppgifterna (sidorna  ,
,  och vinkeln
och vinkeln  ). Precis som i det föregående exemplet är det enklast att först beräkna vinkeln vid
). Precis som i det föregående exemplet är det enklast att först beräkna vinkeln vid  , eftersom summan av vinklarna i en triangel alltid är
, eftersom summan av vinklarna i en triangel alltid är  . Därför är
. Därför är
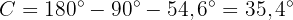
Denna gång är hypotenusan inte given, så vi måste använda tangens:
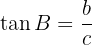
Därför är
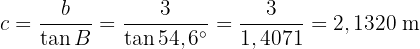
Eftersom 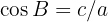 , gäller även
, gäller även
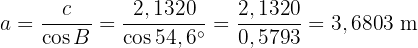
På så sätt har vi nu beräknat alla saknade mått.
Givet är den rätvinkliga triangeln ABC med den räta vinkeln vid  . Vi vet att
. Vi vet att  och
och 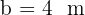 . Beräkna den spetsiga vinkeln och den saknade sidans längd.
. Beräkna den spetsiga vinkeln och den saknade sidans längd.
Titta på skissen av triangeln:
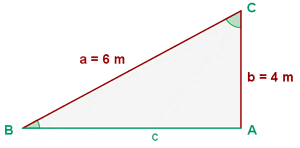
Vi söker kateten  och vinklarna
och vinklarna  och
och  . Enligt Pythagoras sats gäller
. Enligt Pythagoras sats gäller  . Därför är
. Därför är
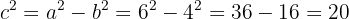
Alltså blir 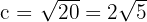 .
.
Vi kan också beräkna vinkeln  :
:
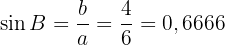
Därmed är 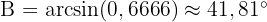 . Eftersom summan av vinklarna i en triangel är
. Eftersom summan av vinklarna i en triangel är  , blir
, blir
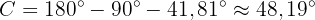
På så sätt har vi beräknat alla saknade mått.
Givet är den rätvinkliga triangeln ABC. Vi vet att 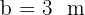 ,
,  och
och 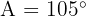 . Bestäm vinklarna och de saknade sidorna.
. Bestäm vinklarna och de saknade sidorna.
Denna gång är triangeln inte rätvinklig. Se triangeln i skissen:
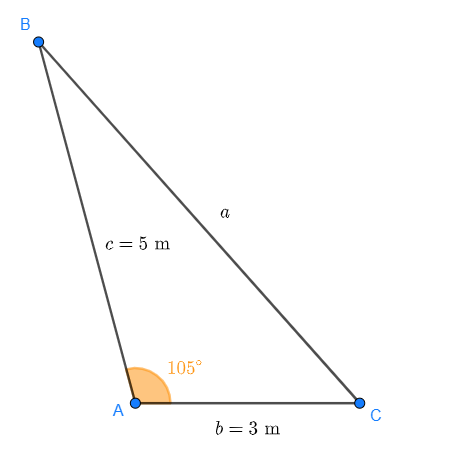
Vi saknar fortfarande vinklarna  ,
,  samt sidan
samt sidan  . Eftersom triangeln inte är rätvinklig kan vi inte använda Pythagoras sats. Däremot kan vi använda cosinussatsen:
. Eftersom triangeln inte är rätvinklig kan vi inte använda Pythagoras sats. Däremot kan vi använda cosinussatsen:
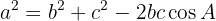
Här har vi alla givna mått:
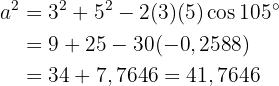
Därmed är 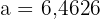 . Med hjälp av sinusatsen kan vi nu beräkna de återstående vinklarna:
. Med hjälp av sinusatsen kan vi nu beräkna de återstående vinklarna:
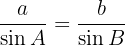
Därmed får vi:
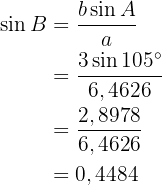
Alltså är 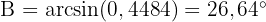 .
.
Slutligen:
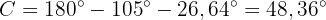
På så sätt har vi bestämt alla mått för triangeln.
Ett 50 meter högt träd kastar en 60 meter lång skugga. Bestäm vinkeln som solen står i just då.
Trädet (sida  ) och skuggan (sida
) och skuggan (sida  ) bildar följande triangel:
) bildar följande triangel:
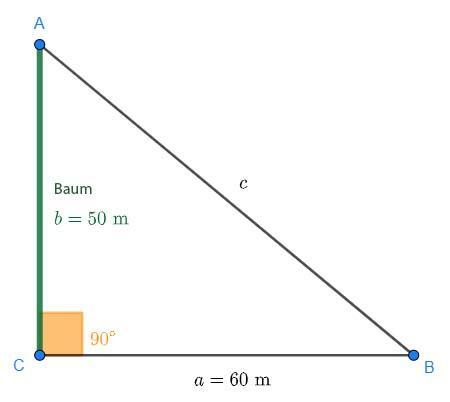
Vi ser att sidan  inte behöver beräknas. Vi söker vinkeln
inte behöver beräknas. Vi söker vinkeln  , vars tangens ges av:
, vars tangens ges av:
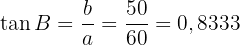
Med hjälp av arctangens får vi:
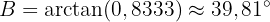
Vi har nu hittat den efterfrågade vinkeln.
En drönare flyger på en höjd av 800 meter. Den filmar en by med en lutningsvinkel (neråt) på 12°. Hur långt måste drönaren flyga i en rak linje, samtidigt som den behåller sin höjd, för att komma precis över byn?
Mellan byn och drönaren bildas följande triangel:
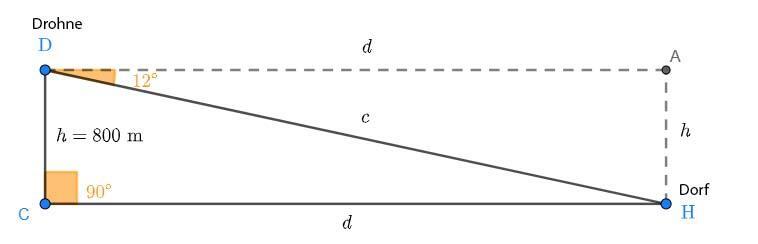
Vi betecknar den okända sträckan med  . Höjden där drönaren flyger betecknas med
. Höjden där drönaren flyger betecknas med  . Lutningsvinkeln motsvarar vinkeln
. Lutningsvinkeln motsvarar vinkeln 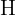 .
.
Tangens för 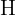 kan beräknas som:
kan beräknas som:
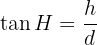
Därmed får vi:
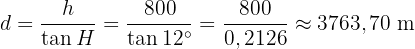
Drönaren måste alltså flyga cirka 3763,70 meter (eller 3,764 km) för att hamna precis över byn.
Bestäm radien på en cirkel med en kordlängd på 24,6 meter och en cirkelbåge på 70°.
Titta på skissen:
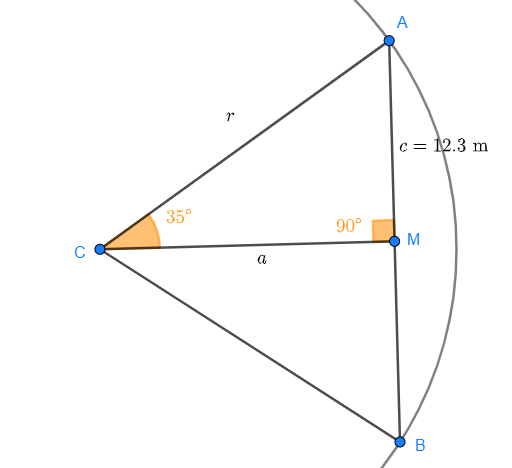
Vi kan se att en rätvinklig triangel bildas med punkterna 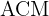 , där
, där  är mittpunkten på cirkelbågen.
är mittpunkten på cirkelbågen.
Radien  är hypotenusan i triangeln. Längden på
är hypotenusan i triangeln. Längden på  är hälften av kordlängden, alltså:
är hälften av kordlängden, alltså:
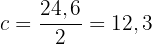
Vinkeln  är hälften av cirkelbågen, alltså
är hälften av cirkelbågen, alltså  . Vi vet att:
. Vi vet att:
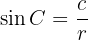
Eftersom  är hypotenusan får vi:
är hypotenusan får vi:
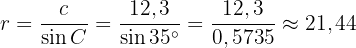
Radien mäter alltså cirka 21,44 meter.
Beräkna arean av en triangel med sidlängderna 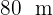 och
och 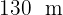 , som bildar en vinkel på 70° mellan dem.
, som bildar en vinkel på 70° mellan dem.
Detta problem kan lösas på flera sätt. Vi kan använda Herons formel för triangelns area eller försöka bestämma höjden. Titta först på skissen av triangeln:
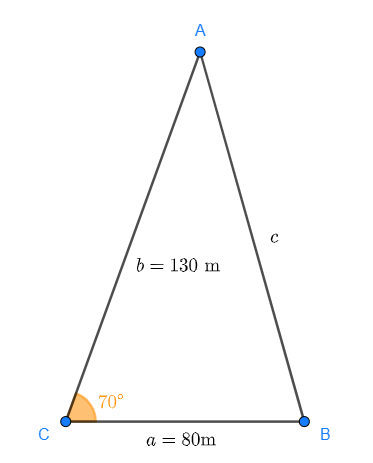
Där är 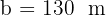 ,
, 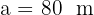 och
och 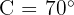 .
.
Om vi ritar höjden vinkelrätt mot  bildas en rätvinklig triangel där
bildas en rätvinklig triangel där  är kateten och
är kateten och  är hypotenusan. Sinus för vinkeln
är hypotenusan. Sinus för vinkeln  är då:
är då:
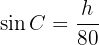
Därmed får vi:
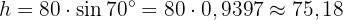
Triangelns area blir alltså:
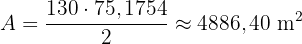
Beräkna höjden på ett träd. Från en punkt i omgivningen kan man se trädets krona under en vinkel på 30° över horisonten. Om man närmar sig trädet  ser man kronan under en vinkel på 60° över horisonten.
ser man kronan under en vinkel på 60° över horisonten.
Titta på skissen till uppgiften:
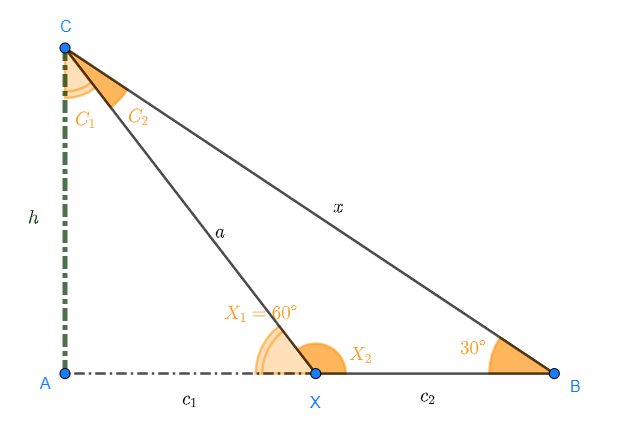
Denna uppgift kan lösas på flera sätt. Ett sätt är att först beräkna sträckan 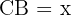 i triangeln
i triangeln  ; därefter använder vi sträckan för att bestämma höjden.
; därefter använder vi sträckan för att bestämma höjden.
För att beräkna triangeln vet vi att vinkeln 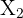 i triangeln
i triangeln  är:
är:
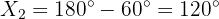
Därefter kan vi använda sinuslagen. Först behöver vi vinkeln 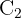 :
:

Med sinuslagen får vi:
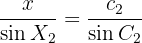
Där:
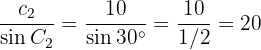
Därmed är:
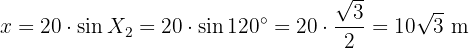
Nu kan vi beräkna höjden. Vi ser att triangeln  är rätvinklig. Därmed gäller:
är rätvinklig. Därmed gäller:
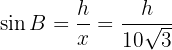
Alltså:
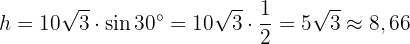
Trädet är alltså cirka 8,66 meter högt.
En regelbunden åttonhörning har en sidlängd på 12 meter. Bestäm radierna för den inskrivna cirkeln och den omskrivna cirkeln.
Titta på åttonhörningen i skissen:
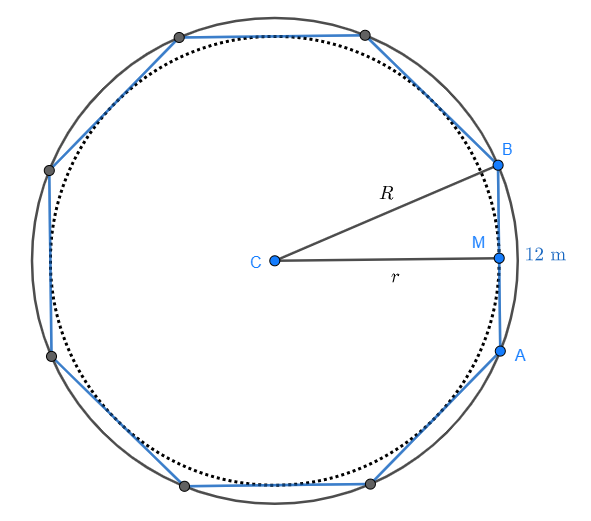
Mellan punkterna  bildas en rätvinklig triangel, där punkten
bildas en rätvinklig triangel, där punkten  är mittpunkten för varje sida av åttonhörningen. Titta på den rätvinkliga triangeln i detalj:
är mittpunkten för varje sida av åttonhörningen. Titta på den rätvinkliga triangeln i detalj:
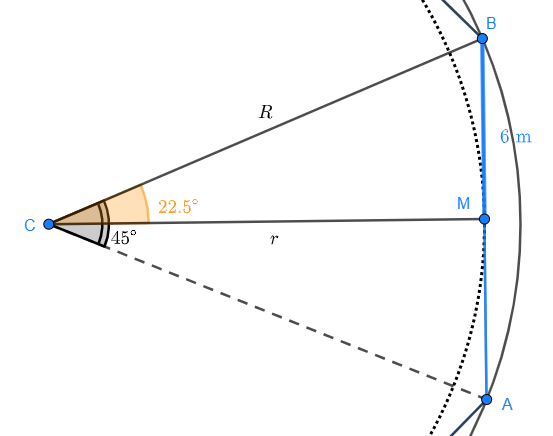
Vi vet att vinkeln 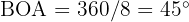 . Vinkeln
. Vinkeln  i den rätvinkliga triangeln är alltså
i den rätvinkliga triangeln är alltså 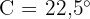 . Dessutom är sidan
. Dessutom är sidan 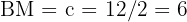 .
.
De två återstående sidorna är lika med radierna för den inskrivna respektive omskrivna cirkeln. För sidan  gäller:
gäller:
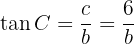
Vi får:
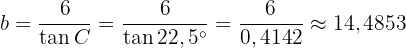
Radien  för den inskrivna cirkeln är alltså cirka 14,49 meter.
för den inskrivna cirkeln är alltså cirka 14,49 meter.
Sidan  uppfyller:
uppfyller:
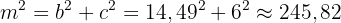
Alltså är 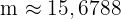 . Radien
. Radien  för den omskrivna cirkeln är alltså cirka 15,68 meter.
för den omskrivna cirkeln är alltså cirka 15,68 meter.
Tre städer 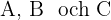 ligger i ett triangelformat mönster och är förbundna med raka vägar. Sträckan från
ligger i ett triangelformat mönster och är förbundna med raka vägar. Sträckan från  till
till  är 12 km, sträckan från
är 12 km, sträckan från  till
till  är 10 km, och vinkeln
är 10 km, och vinkeln 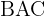 är
är 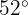 . Bestäm avståndet mellan städerna
. Bestäm avståndet mellan städerna 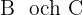 .
.
Titta på triangeln i skissen:
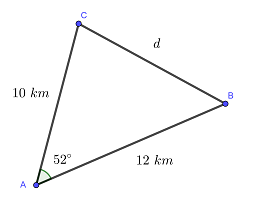
För att beräkna sidan  kan cosinussatsen användas:
kan cosinussatsen användas:
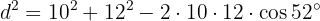
Fortsätt med beräkningen och vi får:
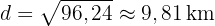
Alltså är avståndet mellan städerna 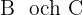 cirka 9,81 km.
cirka 9,81 km.
Peter släpper upp en drake med en 40 m lång lina. Om stigningsvinkeln är 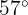 , hur högt flyger draken över marken?
, hur högt flyger draken över marken?
Linan på draken (sida  ) och drakens höjd över marken (sida
) och drakens höjd över marken (sida  ) bildar en rätvinklig triangel:
) bildar en rätvinklig triangel:
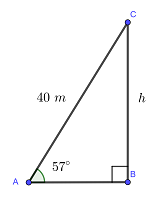
Sinus för vinkeln  kan skrivas som:
kan skrivas som:
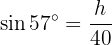
Lös för  :
:
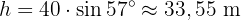
Alltså är drakens höjd över marken cirka 33,55 meter.
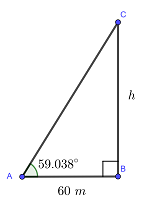
En byggnad kastar en skugga på 60 m när solen står i en vinkel på 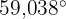 . Hur hög är byggnaden?
. Hur hög är byggnaden?
Byggnaden (sida  ) och skuggan (sida
) och skuggan (sida  ) bildar följande rätvinkliga triangel:
) bildar följande rätvinkliga triangel:
Tangens för vinkeln 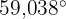 kan skrivas som:
kan skrivas som:
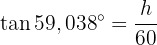
Lös för  :
:
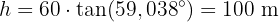
Alltså är byggnadens höjd 100 meter.
Bevisa den trigonometriska likheten för följande ekvationer:
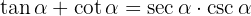 Skriv först
Skriv först 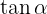 och
och 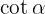 med hjälp av definitionen i sinus och cosinus:
med hjälp av definitionen i sinus och cosinus: 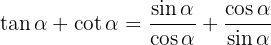
Sätt samman bråken med gemensam nämnare: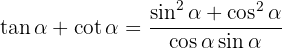
Eftersom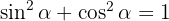 får vi:
får vi: 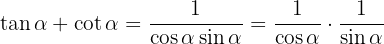
Detta är definitionerna av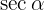 och
och  .
.
Alltså: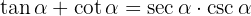
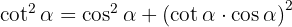
Börja med högra sidan: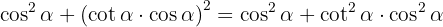
Faktorisera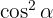 :
: 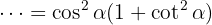
Enligt Pythagoras gäller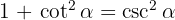 , därför får vi:
, därför får vi: 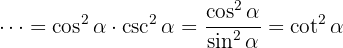
Uppgiften är därmed bevisad.
Börja med högra sidan och faktorisera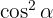 :
: 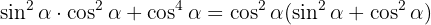
Eftersom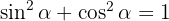 får vi:
får vi: 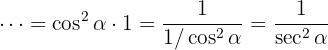
Alltså är uppgiften bevisad.
Bevisa den trigonometriska likheten för följande ekvationer:
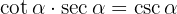
Börja med vänstra sidan och skriv om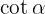 och
och 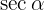 i termer av sinus och cosinus:
i termer av sinus och cosinus: 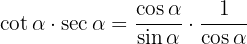
Förenkla bråken: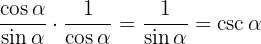
Alltså är ekvationen bevisad.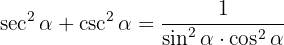
Skriv om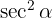 och
och 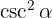 i termer av sinus och cosinus:
i termer av sinus och cosinus: 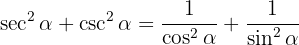
Sätt samman bråken med gemensam nämnare: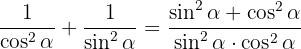
Eftersom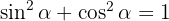 får vi:
får vi: 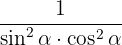
Ekvationen är därmed bevisad.
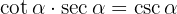 Det enklaste är att börja på vänstra sidan och skriva om i termer av sinus och cosinus:
Det enklaste är att börja på vänstra sidan och skriva om i termer av sinus och cosinus: 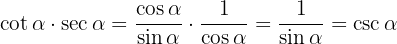
Här tar ut varandra.
ut varandra.
Uppgiften är alltså bevisad i ett steg.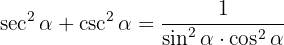
Börja återigen på vänstra sidan och skriv om i termer av sinus och cosinus: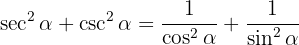
Sätt bråken på gemensam nämnare och summera: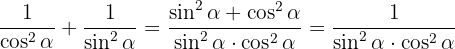
Eftersom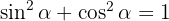 är uppgiften bevisad.
är uppgiften bevisad.
Sammanfatta med AI: