Potenser med rationella exponenter
Beräkna värdena av följande potenser:
1 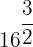
2 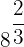
3 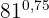
4 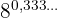
Beräkna värdena av följande potenser:
Lösningar:
En potens med ett bråk som exponent är lika med en rot, vars rotexponent är nämnaren  i bråket och exponenten för radikanden är täljaren
i bråket och exponenten för radikanden är täljaren 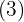 .
.
För att lösa den första uppgiften faktoriserar vi först  , utför de nödvändiga stegen för radikanden och extraherar faktorerna.
, utför de nödvändiga stegen för radikanden och extraherar faktorerna.
1 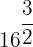
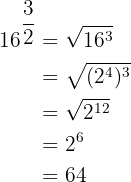
2 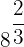
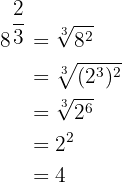
3 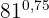
I detta fall omvandlar vi exponenten, som är ett exakt decimaltal, till ett bråk
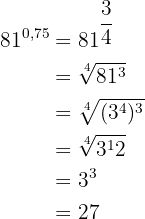
4 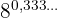
Exponenten, som är ett periodiskt decimaltal, omvandlas till ett bråk
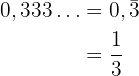
När exponenten är ett bråk kan vi lösa
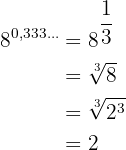
Faktorer under rottecknet
Delvis rotdragning:
1 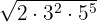
2 
Delvis rotdragning:
Lösningar:
1 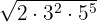
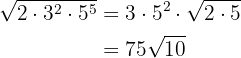
Exponenten för talet två  är mindre än rotexponenten
är mindre än rotexponenten  , därför stannar det kvar under roten.
, därför stannar det kvar under roten.
Exponenten för talet 
 är lika med rotexponenten
är lika med rotexponenten  , därför stannar talet
, därför stannar talet  inte kvar under roten.
inte kvar under roten.
Exponenten för talet 
 är större än rotexponenten
är större än rotexponenten  , därför delas denna exponent med rotexponenten. Kvoten
, därför delas denna exponent med rotexponenten. Kvoten  som vi får blir exponenten för faktorn utanför radikanden, och resten
som vi får blir exponenten för faktorn utanför radikanden, och resten  är exponenten för faktorn innanför radikanden.
är exponenten för faktorn innanför radikanden.
2 
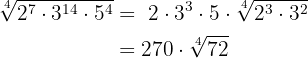
Exponenterna är större än rotexponenten, så dessa exponenter delas med rotexponenten.
Var och en av de erhållna kvoterna är exponenten för motsvarande faktor utanför radikanden, och var och en av de erhållna resterna är exponenten för motsvarande faktor innanför radikanden.
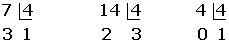
Faktorer utanför radikanden
Vi tittar på faktorerna:
1 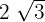
2 
Vi tittar på faktorerna:
Lösningar:
1 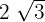
Innan vi börjar med lösningen bör vi påminna oss om några egenskaper hos rötter. Vi vet att roten som tillämpas på en produkt är produkten av rötterna
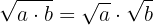
och att rotexponenten för roten, när den omvandlas till exponentiell form, delas med potensen av basen
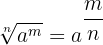
Vi tillämpar alltså dessa två lagar när vi vill förenkla uttryck där rötter förekommer:
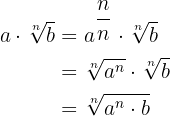
Så kommer vi till resultatet

Detta tillämpar vi nu på vårt problem:
Vi sätter in våra tal och får
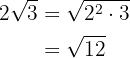
2 
Vi tillämpar vår formel; rotexponenten är här 
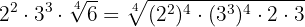
Vi utför de nödvändiga räknestegen
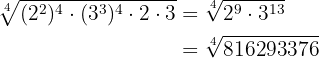
Liknamnade rötter
Vi vill att följande rötter ska vara liknamnade:
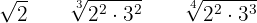
Wurzeln gleichnamig machen:
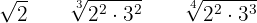
Lösungen:
Wir ermitteln das kleinste gemeinsame Vielfache der Wurzelexponenten, das somit auch der gesuchte Wurzelexponent ist:
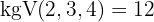
Wir dividieren den gemeinsamen Wurzelexponenten durch jeden der Wurzelexponenten. Die Ergebnisse multiplizieren wir mit den entsprechenenden Exponenten
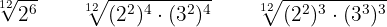
Wir führen die nötigen Rechenschritte durch
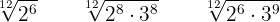
Addition och subtraktion av rötter
Beräkna:
1 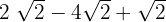
2 
3 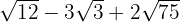
4 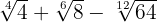
Utför följande beräkningar:
Lösningar:
1 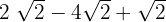
Eftersom rötterna är lika får vi addera och subtrahera koefficienterna för rötterna:
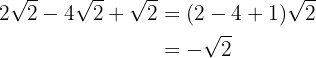
2 
Vi slår samman koefficienterna för rötterna:
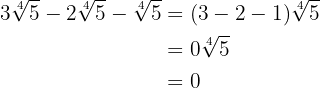
3 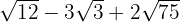
Vi faktoriserar radikanderna, extraherar faktorerna från rötterna (om möjligt) och multiplicerar dem med koefficienten för motsvarande rot
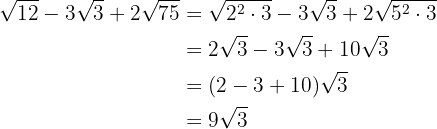
4 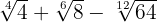
Vi extraherar faktorerna från rötterna och multiplicerar dem med koefficienten för motsvarande rot

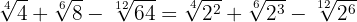
Vi förenklar rötterna. För den första roten dividerar vi rotexponenten och exponenten för radikanden med  , för den andra med
, för den andra med  och för den tredje med
och för den tredje med 
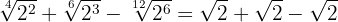
Vi slår samman koefficienterna för rötterna
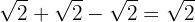
Liknamnade rotexponenter och sammanslagning av rötter
Beräkna:
1 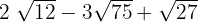
2 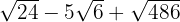
3 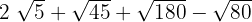
4 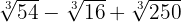
Beräkna:
Lösningar:
Eftersom rötterna inte är lika måste vi följa två steg: Vi faktoriserar rötterna, extraherar faktorer (om möjligt) och multiplicerar dem med koefficienten för motsvarande rot
Vi slår samman koefficienterna för rötterna
1 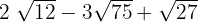
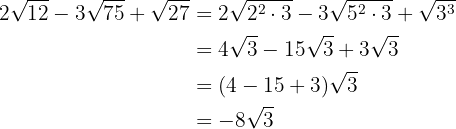
2 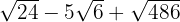
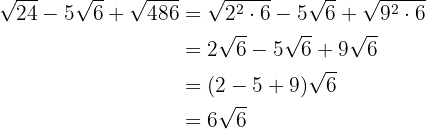
3 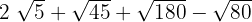
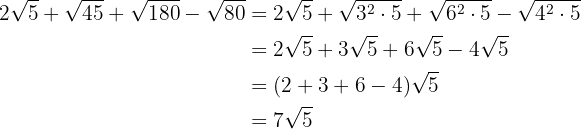
4 
Addition med rötter som står i nämnaren
Beräkna enligt följande:
1 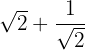
2 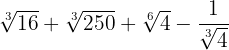
Addera enligt följande:
Lösningar:
1 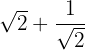
Vi rationaliserar den andra termen genom att multiplicera och dividera med kvadratroten ur 
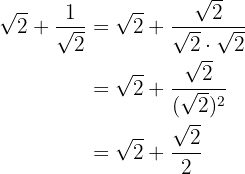
Vi bryter ut den gemensamma faktorn för roten ur  och slår samman
och slår samman
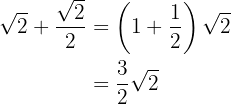
2 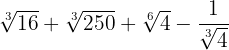
Vi faktoriserar rötterna
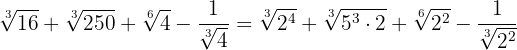
För de första två termerna extraherar vi faktorer, för den tredje förenklar vi roten genom att dividera rotexponenten och exponenten för radikanden med  , och för den sista termen rationaliserar vi genom att multiplicera och dividera med kvadratroten ur
, och för den sista termen rationaliserar vi genom att multiplicera och dividera med kvadratroten ur  .
.
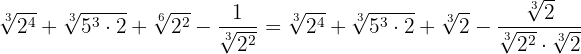
Eftersom alla rötter är lika kan vi slå samman koefficienterna
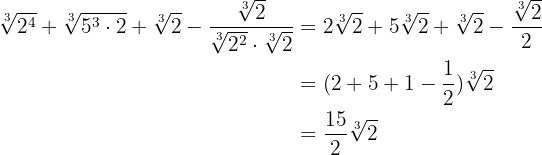
Produkt av rötter
Multiplicera enligt följande:
1 
2 
3 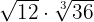
Multiplicera enligt följande:
Lösningar:
1 
Eftersom rötterna har samma rotexponent multiplicerar vi radikanderna och faktoriserar dem för att extrahera faktorerna från roten.
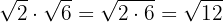
2 
Vi faktoriserar
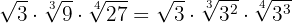
Vi reducerar till en gemensam rotexponent, därför måste vi beräkna den minsta gemensamma multipeln av rotexponenterna, som sedan blir den gemensamma rotexponenten.
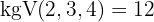
Vi dividerar den gemensamma rotexponenten latex[/latex] med var och en av rotexponenterna  . Det respektive resultatet multiplicerar vi med motsvarande exponenter
. Det respektive resultatet multiplicerar vi med motsvarande exponenter  .
.
Vi bildar produkten av potenser med samma bas i radikanden och extraherar faktorer från radikanden.
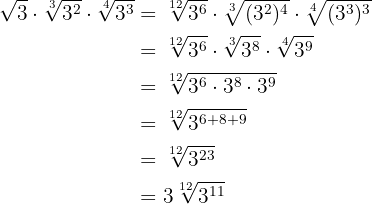
3 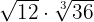
Vi beräknar den minsta gemensamma multipeln av rotexponenterna.
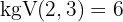
Vi beräknar:
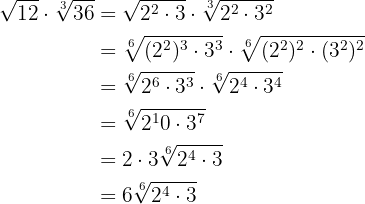
Dividera med rötter
Dividera enligt följande:
1 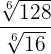
2 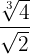
3 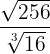
Dividera enligt följande:
Lösningar:
1 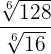
Eftersom rötterna har samma rotexponent dividerar vi radikanderna och förenklar roten genom att dividera rotexponenten och exponenten för roten med 
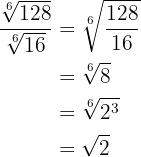
2 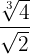
Först reducerar vi till en gemensam rotexponent. Vi måste alltså beräkna den minsta gemensamma multipeln av rotexponenterna, som sedan blir den gemensamma rotexponenten.
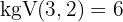 .
.
med var och en av rotexponenterna 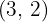 och multiplicerar det respektive resultatet med motsvarande exponenter
och multiplicerar det respektive resultatet med motsvarande exponenter 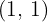 .
.
Vi faktoriserar  så att vi kan utföra divisionen av potenser med samma bas och dividerar:
så att vi kan utföra divisionen av potenser med samma bas och dividerar:
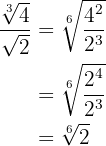
3 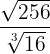
Vi går tillväga på samma sätt som i föregående exempel
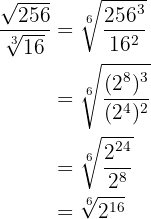
Vi förenklar roten genom att dividera rotexponenten och exponenten för roten med  och extraherar slutligen faktorerna
och extraherar slutligen faktorerna
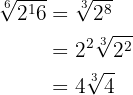
Förenkla följande uttryck
Beräkna:
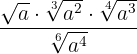
Beräkna:
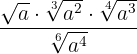
Först beräknar vi den minsta gemensamma multipeln av rotexponenterna, som sedan blir vår gemensamma rotexponent
Vi dividerar den gemensamma rotexponenten latex[/latex] med var och en av rotexponenterna 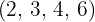 och det respektive resultatet multiplicerar vi med motsvarande exponenter
och det respektive resultatet multiplicerar vi med motsvarande exponenter 
Vi löser upp parenteserna, förenklar bråket och multiplicerar i täljaren potenserna med samma bas
Vi förenklar roten genom att dividera rotexponenten och exponenten för radikanden med 
Slutligen extraherar vi faktorerna
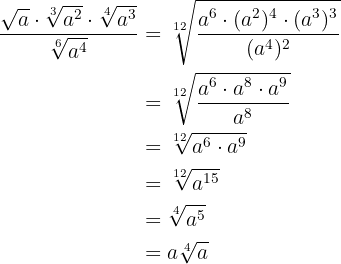
Ordningsföljd vid lösning av rötter
Beräkna:
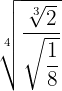
Beräkna:
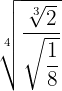
Lösningar:
Först konstaterar vi att 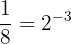 .
.
Vi för rötterna i täljare och nämnare till en gemensam rotexponent.
Vi kvadrerar nämnaren och dividerar potenser med samma bas.
Vi tar nämnaren upphöjt till 3 och utför divisionen av potenser med samma bas.
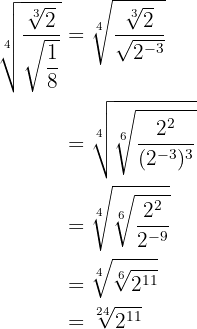
Potenser av en rot
Utför följande räkneoperationer med potenser:
1 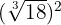
2 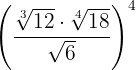
Utför följande räkneoperationer med potenser:
Lösningar:
1 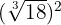
Vi kvadrerar roten, faktoriserar  och kvadrerar den. Till sist extraherar vi faktorerna
och kvadrerar den. Till sist extraherar vi faktorerna
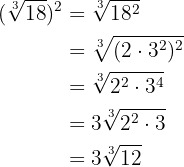
2 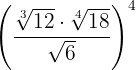
Vi tar radikanderna upphöjt till 4, faktoriserar radikanderna och extraherar talet  ur roten
ur roten
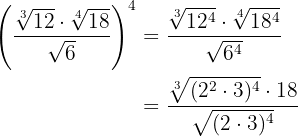
För rötterna utför vi räkneoperationerna med potenser och bestämmer en gemensam rotexponent så att vi kan utföra divisionen
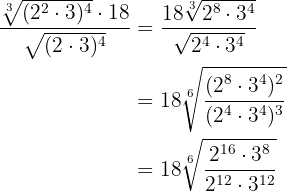
Wir vereinfachen die Wurzel, indem wir den Wurzelexponenten und die Exponenten des Radikanden durch  dividieren, und dividieren Potenzen mit dem gleichen Exponenten
dividieren, und dividieren Potenzen mit dem gleichen Exponenten
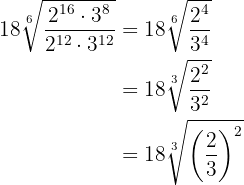
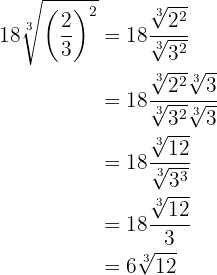
Binom och rötter
Beräkna enligt följande:
1 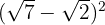
2 
3 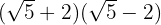
4 
Beräkna enligt följande:
Lösningar:
1 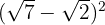
En differens i kvadrat är lika med kvadraten av första termen, minus två gånger första termen gånger andra termen, plus andra termen i kvadrat
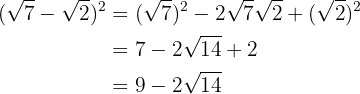
2 
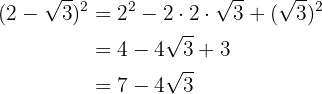
3 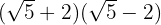
En summa gånger differens är lika med differensen av termerna i kvadrat
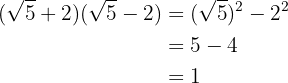
4 
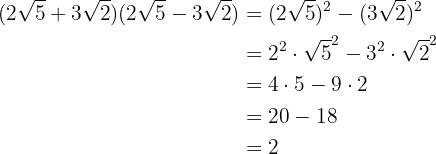
Blandade uppgifter med rötter
Beräkna:
1 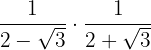
2 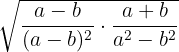
Beräkna:
Lösningar:
1 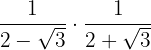
Vi multiplicerar bråken. I nämnaren har vi en summa gånger en differens, vilket är lika med differensen av termerna i kvadrat
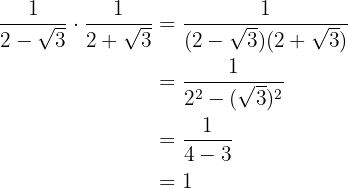
2 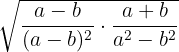
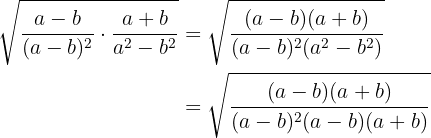
Differensen av termerna i kvadrat i nämnaren bildas som summa gånger differens och bråket förenklas
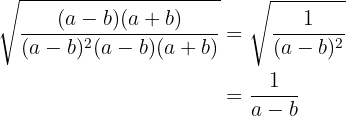
Rötter ur rötter
Beräkna:
1 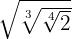
2 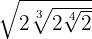
3 
Beräkna:
Lösningar:
1 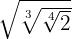
Vi multiplicerar rotexponenterna
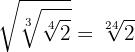
2 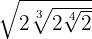
Vi tar den första  med in i kvadratroten. Därför måste vi ta den upphöjt till 3 och multiplicera potenserna med samma bas. Vi fortsätter med detta tillvägagångssätt tills alla värden står under roten och vi kan multiplicera
med in i kvadratroten. Därför måste vi ta den upphöjt till 3 och multiplicera potenserna med samma bas. Vi fortsätter med detta tillvägagångssätt tills alla värden står under roten och vi kan multiplicera  . Slutligen återstår
. Slutligen återstår 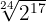 .
.
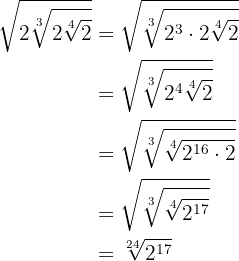
3 
Vi för  under kvadratroten genom att kvadrera. Vi multiplicerar potenserna med samma bas.
under kvadratroten genom att kvadrera. Vi multiplicerar potenserna med samma bas.
Vi multiplicerar rotexponenterna och förenklar genom att dividera rotexponenten och exponenten för radikanden med 3.
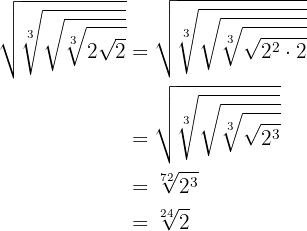
Rationalisera rötter
Rationalisera följande rötter:
1 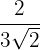
2 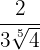
3 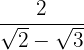
4 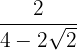
5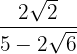
Rationalisera följande rötter:
Lösningar:
1 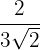
Vi multiplicerar täljare och nämnare med roten ur  , beräknar och förenklar bråket.
, beräknar och förenklar bråket.
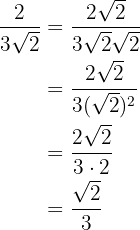
2 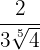
Radikanden  skriver vi som en potens:
skriver vi som en potens:  .
.
Nu måste vi multiplicera täljare och nämnare med den 5:e roten ur  .
.
Vi multiplicerar rötterna i nämnaren, extraherar faktorer och förenklar bråket.
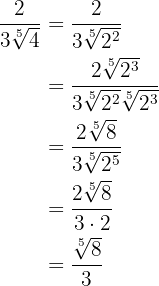
3 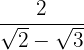
Vi multiplicerar täljare och nämnare med det omvända av nämnaren, löser upp parenteserna i täljaren och adderar med differensen i nämnaren, så att vi får en differens av termerna i kvadrat.
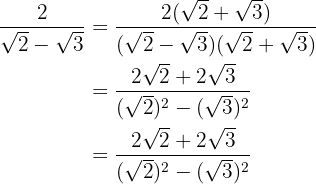
I nämnaren extraherar vi radikanderna och dividerar med  , det vill säga vi ändrar tecknet på täljaren.
, det vill säga vi ändrar tecknet på täljaren.
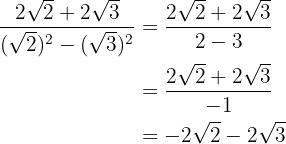
4 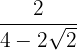
Vi multiplicerar och dividerar bråket med det omvända av nämnaren.
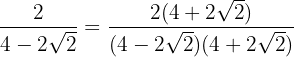
Vi beräknar resultatet av summa gånger differens i nämnaren och får en differens av termerna i kvadrat:
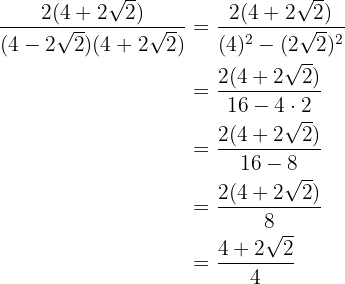
5 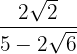
Vi multiplicerar täljare och nämnare med det omvända av nämnaren, löser upp parentesen i täljaren och räknar summa gånger differens. Så får vi en differens av termerna i kvadrat.
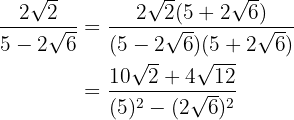
I täljaren faktoriserar vi  och extraherar faktorerna. Därefter utför vi de nödvändiga räknestegen i nämnaren.
och extraherar faktorerna. Därefter utför vi de nödvändiga räknestegen i nämnaren.
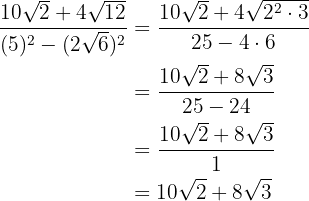
Potenslagar vid räkning med rötter
Rationalisera:
1 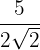
2 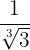
3 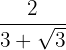
4 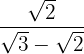
5 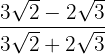
Rationalisera:
Lösningar:
1 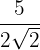
Vi multiplicerar täljare och nämnare med roten ur  och utför de nödvändiga räknestegen
och utför de nödvändiga räknestegen
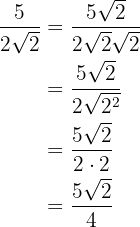
2 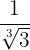
Här måste vi vara uppmärksamma på att vi måste bilda produkten för att kunna lösa upp roten ur 
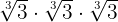
Vi går tillväga enligt följande:
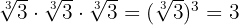
med andra ord, eftersom vi redan har  i nämnaren, behöver vi bara multiplicera med
i nämnaren, behöver vi bara multiplicera med  för att bli av med roten.
för att bli av med roten.
För att inte förändra det numeriska värdet av uttrycket multiplicerar vi både täljare och nämnare med  . Vi får:
. Vi får:
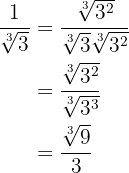
3 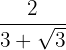
Vi multiplicerar och dividerar bråket med det omvända av nämnaren
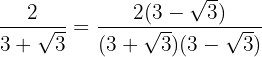
I täljaren löser vi upp parentesen och i nämnaren räknar vi summa gånger differens, så att vi får en differens.
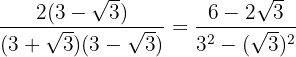
Vi utför de nödvändiga räknestegen och förenklar bråket genom att bryta ut 
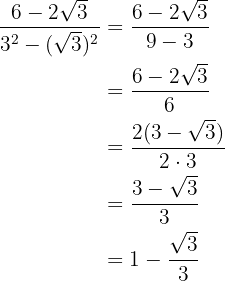
4 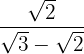
Vi multiplicerar och dividerar bråket med det omvända av nämnaren
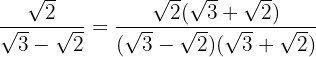
Vi löser upp parentesen i täljaren. I nämnaren räknar vi summa gånger differens och får därför en differens
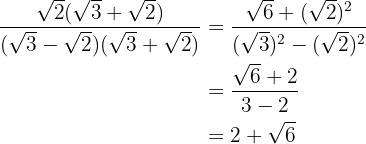
5 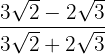
Vi multiplicerar och dividerar bråket med det omvända av nämnaren
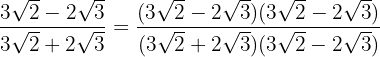
Vi skriver täljaren som en potens
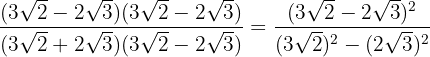
I täljaren har vi en differens i kvadrat, vilket är lika med första termen i kvadrat minus det dubbla av första termen gånger andra termen, plus andra termen i kvadrat. I nämnaren har vi en summa gånger en differens, vilket är lika med differensen av termerna i kvadrat
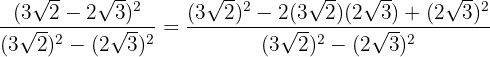
Vi utför de nödvändiga räknestegen och förenklar
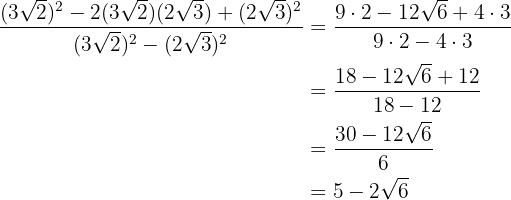
Sammanfatta med AI:


