I denna artikel kommer vi att titta på uppgifter där vi arbetar fram frekvenstabell för ett givet dataset.
Under månaden juli uppmättes följande högsta temperaturer i en stad:
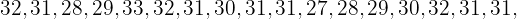
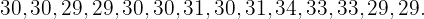
Skapa frekvenstabell till detta. Denna måste innehålla följande: all data, absoluta frekvenser, kumulerade frekvenser, relativa frekvenser och kumulerade relativa frekvenser.
Följande egenskaper finns:
1 I den första kolumnen i tabellen skriver vi variabeln, ordnad i stigande ordning.
2 I den andra kolumnen skriver vi den absoluta frekvensen (hur ofta varje specifikt värde förekommer), nämligen  .
.
3 I den tredje kolumnen skriver vi den kumulerade frekvensen (summan av de absoluta frekvenserna för den aktuella och de föregående variablerna), alltså  .
.
4 Den första raden visar att den absoluta och den kumulerade frekvensen är lika: 
5 För alla rader utom den första raden gäller att den kumulerade frekvensen är lika med den absoluta frekvensen för denna rad plus den kumulerade frekvensen för den föregående raden, alltså
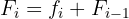
6 Den sista kumulerade frekvensen måste vara lika med  (summan av
(summan av  ), det vill säga
), det vill säga  .
.
7 I den fjärde kolumnen skriver vi de relativa frekvenserna, nämligen  , som fås genom division av de enskilda absoluta frekvenserna med totala antalet data, nämligen
, som fås genom division av de enskilda absoluta frekvenserna med totala antalet data, nämligen  .
.
8 I den femte kolumnen skriver vi den kumulerade relativa frekvensen  .
.
9 Den första raden visar att den kumulerade relativa frekvensen och den relativa frekvensen är lika: 
10 För alla rader utom den första raden gäller att den kumulerade relativa frekvensen är lika med den relativa frekvensen för denna rad plus den kumulerade relativa frekvensen för den föregående raden, alltså
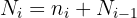
Frekvenstabell ser alltså ut som följer
[table “28” could not be loaded /]
Respektive vikt för  anställda på en fabrik ges av följande tabell
anställda på en fabrik ges av följande tabell
[table “30” could not be loaded /]
Skapa motsvarande frekvenstabell.
Vi observerar att för frekvenstabell måste följande gälla
1 I den första kolumnen i tabellen skriver vi intervallen eller grupperna. Den första kolumnen är alltså komplett.
2 I den andra kolumnen skriver vi den absoluta frekvensen (hur ofta varje specifikt värde förekommer), nämligen  . Denna kolumn är alltså komplett.
. Denna kolumn är alltså komplett.
3 I den tredje kolumnen skriver vi den kumulerade frekvensen (summan av de absoluta frekvenserna för den aktuella och de föregående variablerna), nämligen  .
.
4 Den första raden visar att den absoluta och den kumulerade frekvensen är lika: 
5 För alla rader utom den första raden gäller att den kumulerade frekvensen är lika med den absoluta frekvensen för denna rad plus den kumulerade frekvensen för den föregående raden, alltså
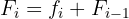
6 Den sista kumulerade frekvensen måste vara lika med  (summan av
(summan av  ), det vill säga
), det vill säga  .
.
7 Den sista kumulerade frekvensen måste vara lika med  (summan av
(summan av  ), det vill säga
), det vill säga  .
.
8 I den femte kolumnen skriver vi den kumulerade relativa frekvensen  .
.
9 För den första raden gäller att den kumulerade relativa frekvensen och den relativa frekvensen är lika: 
10 För alla rader utom den första raden gäller att den kumulerade relativa frekvensen är lika med den relativa frekvensen för denna rad plus den kumulerade relativa frekvensen för den föregående raden, alltså
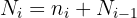
Tabellen ges alltså av
[table “31” could not be loaded /]
En tandläkare observerar hur ofta karies förekommer hos vart och ett av  barn på en viss skola. Den erhållna informationen sammanfattas i nedanstående tabell:
barn på en viss skola. Den erhållna informationen sammanfattas i nedanstående tabell:
[table “32” could not be loaded /]
Komplettera tabellen genom att bestämma värdena för  .
.
Det gäller alltid att summan av alla relativa frekvenser är  . Detta betyder att
. Detta betyder att
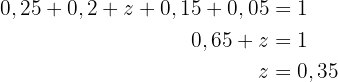
Därför är 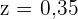 . Därav följer att
. Därav följer att  är den relativa frekvensen för gruppen med
är den relativa frekvensen för gruppen med  gånger karies, medan den absoluta frekvensen är
gånger karies, medan den absoluta frekvensen är  . Vi observerar också att
. Vi observerar också att  är, eftersom det handlar om data från
är, eftersom det handlar om data från  barn. Eftersom alltså den relativa frekvensen är den absoluta frekvensen delat med
barn. Eftersom alltså den relativa frekvensen är den absoluta frekvensen delat med  , utnyttjar vi detta faktum för att bestämma
, utnyttjar vi detta faktum för att bestämma  .
.
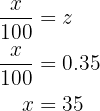
Nu måste vi bara bestämma  , som är den absoluta frekvensen för gruppen med
, som är den absoluta frekvensen för gruppen med  gånger karies. Den relativa frekvensen är
gånger karies. Den relativa frekvensen är 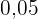 . Eftersom den relativa frekvensen är den absoluta frekvensen delat med
. Eftersom den relativa frekvensen är den absoluta frekvensen delat med  , utnyttjar vi detta faktum för att bestämma
, utnyttjar vi detta faktum för att bestämma  .
.
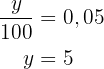
Nu har vi all nödvändig data för att komplettera tabellen
[table “33” could not be loaded /]
Komplettera den statistiska tabellen med den saknade datan:
[table “34” could not be loaded /]
Vi löser steg för steg och bestämmer först värdet för  . Därefter kan vi bestämma de resterande saknade värdena.
. Därefter kan vi bestämma de resterande saknade värdena.
1 Som första steg bestämmer vi värdet för  .
.
För att bestämma värdet för  utnyttjar vi den första raden. Vi minns att den relativa frekvensen är den absoluta frekvensen delat med
utnyttjar vi den första raden. Vi minns att den relativa frekvensen är den absoluta frekvensen delat med  . Eftersom den absoluta frekvensen är
. Eftersom den absoluta frekvensen är  och den relativa frekvensen är
och den relativa frekvensen är 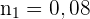 , utnyttjar vi dessa data för att bestämma
, utnyttjar vi dessa data för att bestämma 

2 Den första raden är enkel. Det saknas bara den kumulerade frekvensen  . Eftersom det handlar om den första raden (första klassen), motsvarar denna därför den absoluta frekvensen
. Eftersom det handlar om den första raden (första klassen), motsvarar denna därför den absoluta frekvensen

3 Andra raden. Som första steg bestämmer vi den kumulerade frekvensen och minns att för denna gäller följande

Nu kan vi bestämma den relativa frekvensen, eftersom vi redan har den absoluta frekvensen
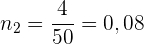
4 Tredje raden. Det saknas bara den absoluta frekvensen. Denna kan vi bestämma med hjälp av den kumulerade eller den relativa frekvensen. Vi utnyttjar den kumulerade frekvensen

5 Fjärde raden. Nu behöver vi bara den kumulerade frekvensen och denna beräknar vi direkt

6 Femte raden. Vi behöver bara den relativa frekvensen och denna beräknar vi direkt
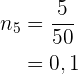
7 Sjätte raden. Det saknas den absoluta och den relativa frekvensen. Den absoluta frekvensen beräknar vi med hjälp av den kumulerade frekvensen.

Nu beräknar vi den relativa frekvensen direkt med hjälp av den absoluta frekvensen
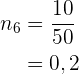
8 Sjunde raden. Det saknas den relativa frekvensen. Vi beräknar direkt
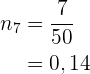
9 Åttonde raden. Här saknas all data. Som första steg bestämmer vi den kumulerade frekvensen. Eftersom det handlar om den sista raden, är den kumulerade frekvensen  . Därför gäller
. Därför gäller  Nu bestämmer vi den absoluta frekvensen med hjälp av den kumulerade frekvensen
Nu bestämmer vi den absoluta frekvensen med hjälp av den kumulerade frekvensen  Slutligen får vi den relativa frekvensen
Slutligen får vi den relativa frekvensen 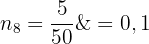
Därmed ges tabellen av
[table “35” could not be loaded /]
Sammanfatta med AI:


