Addera polynom
För att få en summa av två eller flera polynom måste koefficienterna för de termer vars okända är lika adderas. Det betyder att variablerna och exponenterna för de termer som ska adderas måste vara lika.
Metod 1 för addition av polynom
Stag:
1 Ordna polynomen efter avtagande grad.
2 Gruppera monomier av samma grad.
3 Addera likartade monomier.
Exempel 1 på addition av polynom
Addera polynom
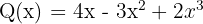
1 Vi ordnar polynomen, om de inte redan är det.
2 Vi grupperar monomierna av samma grad.
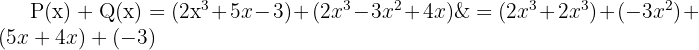
3 Vi adderar likartade monomier.
Metod 2 för addition av polynom
Vi kan också addera polynom genom att helt enkelt skriva dem under varandra. Och det på så sätt att de likartade monomierna befinner sig i kolumner och således kan adderas.
Exempel på metod 2
Addera följande polynom
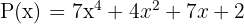
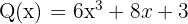
1 Vi skriver termerna i avtagande ordning i kolumner och adderar.
Således
2 
Subtrahera polynom
Vid polynomsubtraktion adderas motsatsen till subtrahenden till minuenden.
Exempel på polynomsubtraktion
Subtrahera följande polynom
1 Vi erhåller motsatsen till subtrahenden 
.
2 Vi grupperar.
3 Resultatet av subtraktionen.
Multiplicera polynom
1. Multiplicera ett tal med ett polynom
Multiplikation av ett tal med ett polynom ger ett annat polynom. Det erhållna polynomet har samma grad som ursprungspolynomet. Koefficienterna för det resulterande polynomet är produkten av koefficienterna för ursprungspolynomet och talet som står framför parentesen. Variablerna förblir desamma.
Exempel:
1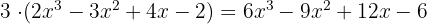 
2 
2. Multiplicera ett monom med ett polynom
Vid multiplikation av ett monom med ett polynom multipliceras monomet med varje enskild monom i polynomet.
Vi kommer ihåg att vi alltid först måste multiplicera tecknen innan vi multiplicerar de tillhörande monomierna. Därtill måste koefficienterna och slutligen den okända multipliceras. Härvid adderas exponenterna vid multiplikation av samma variabler.
Exempel:
3. Multiplicera polynom
Denna räkneoperation kan utföras på olika sätt.
Metod 1 för multiplikation av polynom
Steg:
1 Varje monom i det första polynomet multipliceras med alla element i det andra polynomet.
2 Monomier av samma grad adderas och man erhåller ett annat polynom, vars grad är summan av graderna för de polynom som multipliceras.
Exempel:
Multiplicera följande polynom
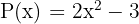
1 Varje monom i det första polynomet multipliceras med alla element i det andra polynomet.
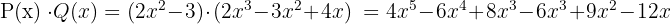
2 Polynom av samma grad adderas.
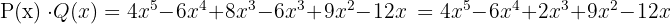
3 Vi erhåller ett annat polynom, vars grad är summan av graderna för de polynom som multipliceras.
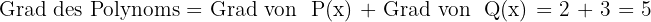
und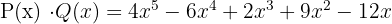
Metod 2 för multiplikation av polynom
Vi kan också multiplicera polynom genom att skriva dem under varandra. I varje rad multipliceras varje monom i det andra polynomet med alla monomier i det första polynomet. Likartade monomier grupperas i samma kolumn och slutligen adderas de likartade monomierna.
Exempel:
Multiplicera följande polynom
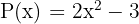
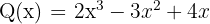
Eftersom kommutativlagen gäller för multiplikation av polynom tar vi som det polynom vi multiplicerar med det enklaste polynomet.
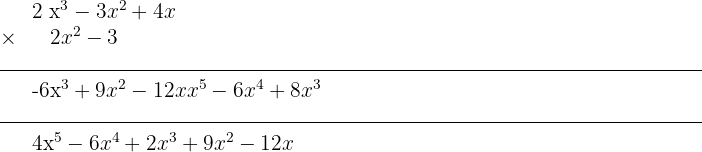
Dividera polynom
Vi börjar förklaringen med ett exempel.
Exempel:
Dividera följande polynom
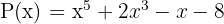
P(x) : Q(x)
1 På vänster sida placerar vi dividenden. Om polynomet inte är komplett lämnar vi en lucka på motsvarande ställen.
2 Divisorn skriver vi till höger i en ruta.
3 Vi dividerar det första monomet i dividenden med det första monomet i divisorn.
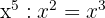
4 Vi multiplicerar varje term i divisorns polynom med det föregående resultatet och subtraherar det från dividendens polynom:
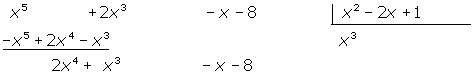
5 Vi dividerar ännu en gång det första monomet i dividenden med det första monomet i divisorn. Resultatet multiplicerar vi med divisorn och subtraherar det från dividenden.
vi erhåller
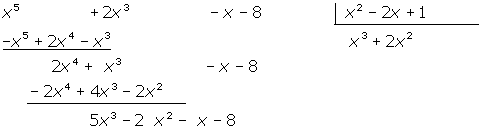
6 Vi går tillväga på samma sätt som tidigare. Och denna gång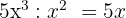 
alltså
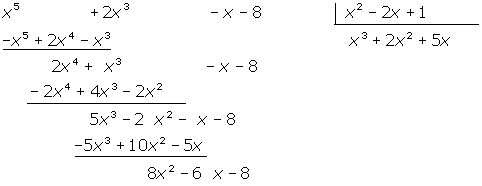
7 Som i de föregående stegen dividerar vi 
med 
och erhåller 
. Vi multiplicerar varje term i divisorn med och erhåller:
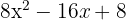
Med resten förfarar vi enligt följande:
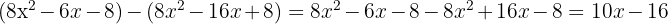
Vi konstaterar att 10x − 16 är resten, eftersom dess grad är lägre än divisorns. Vi kan därför inte dividera vidare. Kvoten är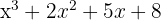 
Behöver du mattehjälp? På Superprof hittar du mattelärare nära dig!
Gillade du den här artikeln? Betysätt den!
Loading...
