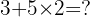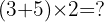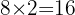Skriftlig räkning är en grundläggande färdighet inom matematiken som eleverna lär sig redan i grundskolan och som är viktig för elever i alla årskurser. Det är en metod som gör det möjligt att lösa matematiska uppgifter skriftligt, oavsett om det gäller addition, subtraktion, multiplikation eller division. Behöver du extra stöd kan mattehjälp göra stor skillnad.
I grund och botten behärskar jag bara dessa fyra grundläggande matematiska operationer: addition, subtraktion, frustration, kapitulation.
Anonym
Skriftlig matematik är mer än bara en teknisk process; den främjar logiskt tänkande och problemlösningsförmåga. Denna artikel kommer inte bara att förklara de olika teknikerna för skriftlig matematik – addition, subtraktion, multiplikation och division – i detalj, utan också ge praktiska tips och tricks som underlättar hanteringen av dessa räknesätt.
Oavsett om det handlar om addition med överföring, subtraktion med komplementmetoden, multiplikation av stora siffror eller division med rest – med den här artikeln lär du dig metoderna för att klara var och en av dessa uppgifter.

Skriftlig addition
Skriftlig addition bör ingå i allmänna kunskaper i matematik. Det är processen där två eller flera tal summeras genom att man skriver dem under varandra och summerar dem från höger till vänster, det vill säga från entalsställningen till de högre siffrorna. Summan skrivs sedan under strecket på samma plats. På så sätt kan man enkelt och steg för steg summera även stora tal.
Skriftlig addition med överföring
Men vad händer om siffran som jag måste skriva under strecket har mer än en siffra? Om summan av siffrorna är större än nio måste en överföring läggas till nästa siffra till vänster. Till exempel vid addition av 467 och 589: Man adderar först entalsiffrorna (7+9=16), skriver 6 under entalsiffrorna och överför 1 till tiotalssiffrorna, där man sedan adderar 6, 8 och den överförda 1 (15) och så vidare.
Skriftlig addition med komma / decimaltal
Vid addition av decimaltal är det viktigt att placera kommatecknen exakt under varandra. Till exempel: 47,5 + 3,75. Rikta in siffrorna så att decimalerna stämmer överens och addera som vanligt, med kommatecknet direkt under kommatecknet i summan.
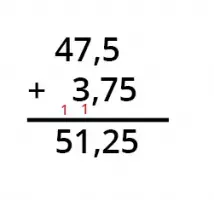
Till exempel: 47,5 + 3,75. Rikta in siffrorna så att decimalerna stämmer överens och lägg ihop som vanligt, med kommatecknet direkt under kommatecknet i summan. Räkna alltså från höger till vänster 0+5=5, 7+5=12 (skriv alltså 2 och överför 1), sedan kommer kommatecknet, 7+3+1=11 (skriv återigen 1 och överför 1) och 4+1=5. Resultatet av 47,5+3,75=51,25.
Med några övningar och textuppgifter kommer du snart att ha lätt för skriftlig addition, oavsett om det är med decimaler, överföringar eller stora siffror.
Skriftlig subtraktion
Skriftlig subtraktion är en grundläggande matematisk färdighet som gör det möjligt att dra ett tal från ett annat genom att skriva dem under varandra och dra dem från varandra på rätt plats. Detta introduceras i grundskolan och är viktigt för att förstå mer avancerade matematiska begrepp.
På samma sätt som vid addition går du här från höger till vänster och drar det nedre talet från det översta. För 1785-562 gör du alltså så här: 5-2=3, 8-6=2, 7-5=2, 1-0=1. 1785-562=1223.
Skriftlig subtraktion med överföring
Subtraktion med överföring uppstår när siffran i det subtraherande talet (subtrahend) vid en punkt är större än motsvarande siffra i det tal som ska subtraheras (minuend). För att lösa denna situation ”lånar” man en tiotal från det närmast högre talet i minuenden. Detta tiotal läggs till minuenden på den lägre platsen och minuenden på den högre platsen minskas med ett.
Addition: Summand+Summand=Summa
Subtraktion: Minuend-Subtrahend=Differens
Multiplikation: Faktor x Faktor=Produkt
Division: Dividend/Divisor=Kvot
Låt oss ta subtraktionen 705 - 387 som exempel. Vi börjar med ental: 5 är mindre än 7. Därför lånar vi en tiotal från tiotalet (0), vilket gör detta tal till -1. För att kompensera för detta lägger vi till 10 till entalen, vilket gör 5 till 15. Nu kan man dra 7 från 15, vilket ger 8.
I tiotalet har man nu -1, vilket innebär att man lånar ytterligare en tiotalsenhet från hundratalet (7). Detta minskar 7 till 6, och tiotalet blir 9. Dra nu 8 från 9, vilket ger 1. På hundratalsidan subtraherar man helt enkelt 3 från 6, vilket ger 3. Slutresultatet blir 318.
Skriftlig subtraktion med decimaler
Vid subtraktion av decimaler, även kallade kommatal, är det precis som vid addition viktigt att placera decimalerna exakt under varandra för att säkerställa korrekt inriktning av decimalerna.
Exempel: 15,75 - 3,2 justeras till 15,75 - 3,20 innan subtraktionen utförs.
Börja subtraktionen från höger till vänster, så att decimaltecknet i lösningen hamnar exakt under de andra decimaltecknen.
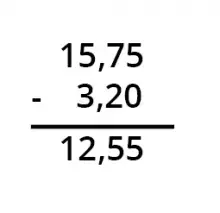
Skriftlig subtraktion: subtraktionsmetoden / kompletteringsmetoden
I den klassiska subtraktionsmetoden subtraheras varje siffra i den nedre siffran från motsvarande siffra i den övre. Om en siffra är mindre än den underliggande krävs en överföring. I kompletteringsmetoden beräknar man däremot vilket värde som måste läggas till den nedre siffran för att nå den övre. Detta kan förenkla uppgiften och är särskilt användbart vid mer komplexa siffror.
Skriftlig division
Skriftlig division är en viktig matematisk färdighet som gör det möjligt att dela ett tal med ett annat för att få fram ett resultat och eventuellt en rest. Denna färdighet används ofta i matematikprov i tillämpade uppgifter. Vid skriftlig division går man tillväga i tre steg.
- Dela det första siffran från vänster i det vänstra talet (dividenden) med det högra talet (delaren).
- Multiplicera delresultatet med delaren och skriv det med ett minustecken under det vänstra talet.
- Skriftlig subtraktion

Om vi till exempel har uppgiften 853:4, börjar vi med steg 1 och räknar 8:4=2. 2 är alltså vårt första delresultat, som vi skriver bakom =. Nu fortsätter vi med steg 2 och beräknar vårt delresultat dividerat med divisorn, alltså 2*4=8. Vi skriver nu 8 med ett minus under det första siffran till vänster om vår dividende och sedan är vi redan vid steg 3, subtraktionen. 8-8=0.
Nu tar vi nästa siffra i vår dividend (dvs. 5) och börjar om från början.
Först skriver vi 5 bredvid resultatet av vår subtraktion, dvs. bredvid 0. Sedan börjar vi om med steg 1: 5 dividerat med 4 är 1, eftersom 4 bara passar in 1 gång i 5.
1 är alltså vårt nästa delningsresultat och skrivs bredvid 2 från förut. 1*4=4 och så skriver vi 4 med ett minus under 5 och fortsätter med subtraktionen. 5-4=1 och vi skriver 1 nedanför och drar ner den sista siffran i vår dividende (3).
Eftersom vi nu har kommit till den sista siffran i dividenden måste vi räkna med allt som står under strecket. Alltså med 13. 13:4=3, så 3 är vårt sista delresultat. 3*4=12, vi skriver 12 med ett minus under 13 och då återstår 1. Det är vår rest. Vi skriver den helt enkelt med ett R framför vårt resultat. Så blir lösningen 853:4=213R1.
Skriftlig division med decimaler
När man dividerar decimaler placerar man decimaltecknet i kvoten direkt över decimaltecknet i dividenden så snart dividenden är helt uppdelad. Om det behövs kan dividenden utökas med nollor för att fullborda divisionen. Exempel: 12,4 dividerat med 2 ger 6,2.
Skriftlig division med stora tal
Division av stora tal följer samma procedur, men kräver fler steg och större noggrannhet. Det är hjälpsamt att dela upp talen i mindre, hanterbara segment och stegvis subtrahera divisorn från den största siffran i dividenden.
Skriftlig multiplikation
Skriftlig multiplikation är en grundläggande metod i matematiken som gör det möjligt för elever att multiplicera stora siffror med varandra genom att beräkna dem stegvis. Denna förmåga är till exempel mycket viktig vid omräkning av måttenheter. För den som vill öva mer kan mattehjälp online vara ett smidigt alternativ.
Skriftlig multiplikation
För att multiplicera skriftligt skriver du först upp beräkningen. Siffran till vänster är multiplikatorn och siffran till höger är multiplikanden. Du börjar med att multiplicera multiplikatorn med den främsta siffran i multiplikanden. Du drar en streck under hela uppgiften och skriver delresultatet under. Fortsätt på samma sätt med de andra siffrorna i multiplikanden. Slutligen lägger du ihop alla delresultat för att få det slutliga resultatet.
Om du nu vill räkna ut 134*12, räknar du först ut 1*134. Det blir 134. Du drar en streck under uppgiften och skriver ner detta delresultat så att den sista siffran (dvs. 4) står precis under den första siffran i multiplikanden. Sedan fortsätter du och räknar ut 134*2=268. Du skriver nu 268 en plats till höger under delresultatet från tidigare (134). Sedan lägger du ihop skriftligt och får 1608. 134*12=1608.
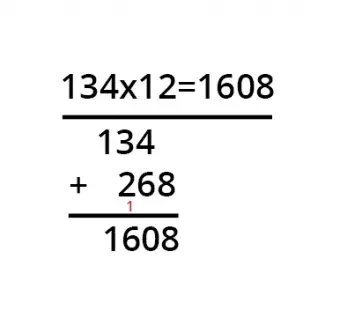
Skriftlig multiplikation med decimaltecken
När du multiplicerar decimaltal måste du först flytta så många siffror åt höger att det inte finns några decimaltecken kvar i siffrorna. När du har utfört multiplikationen enligt beskrivningen ovan placerar du decimaltecknet i resultatet så att antalet decimaler motsvarar summan av decimalerna i de två ursprungliga talen. Till exempel: 12,3 multiplicerat med 3,4 ger 41,82 eftersom båda talen tillsammans har två decimaler.
Sammanfatta med AI:















 .
.