I vår värld, där siffror påverkar alla aspekter av vardagen – från att mäta tid och hantera finansiella medel till att utvärdera vetenskapliga data – är förståelsen för stora siffror oumbärlig för matematisk allmänbildning. Miljoner, miljarder och ännu större siffror är inte bara abstrakta begrepp, utan också grundläggande verktyg för att navigera i det moderna livet.
Inom matematiken kommer vi ständigt i kontakt med sådana storleksordningar, vare sig det gäller inlärning, beräkning eller analys av data. En miljon, till exempel, ett tal med sex nollor, används ofta som språngbräda till ännu större tal som miljard (nio nollor) eller biljon (tolv nollor).
| Namn | Antal | Antal nollor |
|---|---|---|
| 1 Miljard | 1 000 000 000 | 9 |
| 1 biljon | 1 000 000 000 000 | 12 |
| 1 biljard | 1 000 000 000 000 000 | 15 |
| 1 biljon | 1 000 000 000 000 000 000 | 18 |
| 1 kvintillion | 1 000 000 000 000 000 000 000 | 21 |
| 1 kvadrillion | 1 000 000 000 000 000 000 000 000 | 24 |
| 1 kvadrillion | 1 000 000 000 000 000 000 000 000 000 | 27 |
| 1 kvintillion | 1 000 000 000 000 000 000 000 000 000 000 | 30 |
| 1 kvintillion | 1 000 000 000 000 000 000 000 000 000 000 000 | 33 |
| 1 sextillion | 1 000 000 000 000 000 000 000 000 000 000 000 000 | 36 |
| 1 sextillion | 1 000 000 000 000 000 000 000 000 000 000 000 000 000 | 39 |
| 1 septillion | 1 000 000 000 000 000 000 000 000 000 000 000 000 000 000 | 42 |
| 1 septillion | 1 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 | 45 |
| 1 oktillion | 1 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 | 48 |
| 1 oktillion | 1 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 | 51 |
Men vad är egentligen det största talet? Teoretiskt sett är tal oändliga, och matematiker kan alltid hitta ett tal som är en enhet större än det hittills största kända talet. I praktiken används dock ofta begreppet ”googol” – en 1 följd av hundra nollor – för att illustrera storleken på vår föreställningsförmåga. Detta leder oss till en annan intressant fråga: Hur kan vi förstå och korrekt återge sådana enorma storlekar?

Skriva och läsa stora siffror
Att korrekt skriva och läsa stora tal är en grundläggande färdighet i matematik och en förutsättning för att kunna räkna med stora tal. För att behärska stora tal är det viktigt att förstå begreppen ”ställningsvärde” och ”ställningsvärdetabell”. En miljon – som består av en 1 med sex nollor – bör skrivas som ”1 000 000” för att säkerställa tydlighet i framställningen. Miljarder och biljoner följer ett liknande mönster, där en miljard skrivs som ”1 000 000 000” och en biljon som ”1 000 000 000 000”.
Det finns flera sätt att skriva stora siffror som till exempel en miljon för att göra dem lättare att läsa. Nollorna delas upp i grupper om tre:
Med mellanslag: 1 000 000
Med punkter: 1 000 000
I ordform: en miljon
Förkortat med siffra: 1 miljon
När man läser dessa siffror är det viktigt att dela upp siffrorna i grupper. Varje grupp representerar tusental, hundratal eller tiotal, vilket underlättar läsningen. Till exempel läses ”123 456 789” som ”hundratjugotre miljoner fyrahundrafemtiofem tusen sjuhundraåttionio”.
Metriska prefix för stora tal
Metriska prefix underlättar förståelsen och hanteringen av stora tal i matematik och i vardagen.
Från ”kilo” (tusen) över ”mega” (miljon) och ”giga” (miljard) till ”tera” (biljon) gör dessa prefix det möjligt för oss att arbeta med enorma storlekar utan att ständigt behöva skriva eller uttala många nollor.
Till exempel representerar ett kilogram tusen gram, medan en gigabyte motsvarar en miljard byte. Dessa prefix är inte bara allmänt förekommande inom naturvetenskapen, utan också inom teknik och ekonomi, där de används för att beskriva datavolymer, frekvenser och kapaciteter. Inom datavetenskap avser terabyte och petabyte kapaciteten hos hårddiskar eller mängden genererade data när det gäller lagring, hantering och analys av datamängder.
Det är därför nödvändigt att lära sig och använda dessa prefix för att effektivt kunna hantera och använda siffror och potenser i stora tal. De fungerar som praktiska verktyg för att minska komplexiteten i talen och förenkla hanteringen av dem, vilket är avgörande inom många vetenskapliga och tekniska områden.
Förståelse för storleksordningen
Stora tal är ofta svåra att greppa, men att visualisera dem kan hjälpa till att utveckla en bättre förståelse för deras dimensioner och ämnet. En miljon är till exempel ett tal som vi ofta hör – vare sig det gäller folkmängd, antalet stjärnor på himlen eller till och med antalet steg man går under ett år. Att visualisera en miljon kan innebära att man föreställer sig en fotbollsstadion som är fylld tio gånger, eftersom en stor stadion rymmer cirka 100 000 åskådare.

Ännu tydligare blir det med en miljard. För att visualisera en miljard kan man föreställa sig att man varje dag, i cirka 2,7 år, spenderar en miljon euro. Detta tydliggör den enorma skillnaden mellan en miljon och en miljard och visar hur viktigt det är att förstå dessa storleksordningar korrekt.
Ett annat exempel är användningen av ”miljarder” inom vetenskapen, till exempel antalet celler i en människokropp eller avståndet mellan stjärnor i ljusår. Sådana sammanhang hjälper till att lära sig hantera siffror och uppskatta deras värde, vilket är oumbärligt för matematiken.
I vardagen möter vi dessa siffror på många olika sätt, vare sig det är genom antalet byte i datorer (gigabyte, terabyte) eller genom folkmassorna vid stora evenemang. Även i matematikundervisningen kan stora siffror förekomma gång på gång i textuppgifter. För den som vill öva mer eller få stöd finns även mattehjälp. Visualiseringen och det praktiska exemplet gör inte bara platsvärdet begripligt, utan lär oss också att räkna med siffrorna på ett naturligt sätt och förstå dem.
Hur många nollor har en miljon?
En miljon har sex nollor. Denna enkla fakta är en grundläggande del av matematisk förståelse och spelar en central roll i platsvärdestabellen, ett oumbärligt verktyg för att lära sig och jämföra stora tal. Platsvärdestabellen hjälper till att sätta varje siffra i ett stort tal i sitt rätta sammanhang, från entalsställena till höger till miljoner och mer till vänster.
har sex nollor
Till exempel visas siffran 1 000 000 i en positionstabell så att ’1’ står i kolumnen för miljoner och följs av sex nollor som representerar tusentals, hundratals, tiotals och entals. Detta system gör det inte bara möjligt att enkelt förstå stora tal som miljoner, miljarder eller till och med biljoner, utan också att jämföra dem effektivt. Genom att jämföra siffrorna kan man snabbt se att en miljard (1 000 000 000) har tre nollor mer än en miljon.

Det största talet
I matematikens värld stöter vi ofta på otroligt stora tal som utmanar vår föreställningsförmåga. Ett framträdande exempel är googol, ett 1 följt av hundra nollor. Ännu större är googolplex, som definieras som 1 följt av ett googol nollor. Dessa tal är inte bara matematiska kuriositeter, utan har också praktiska tillämpningar inom teorin om stora tal och inom datavetenskap, särskilt inom kryptografi och algoritmteori.
Den vetenskapliga och matematiska betydelsen av dessa enorma tal ligger i deras förmåga att illustrera begrepp som oändlighet och tillväxt av potenser. De erbjuder en plattform där matematiker kan utforska gränserna för det räknbara och talteorin. I matematiken är tal i princip oändliga, vilket innebär att det alltid finns ett tal som är ännu större än alla tidigare definierade tal.
Användning av stora tal i den verkliga världen
Stora tal möter vi inte bara i teorin, utan också praktiskt i många områden av vardagen, vetenskapen och ekonomin. Inom astronomin är stora tal till exempel allestädes närvarande när det gäller avstånd mellan stjärnor och galaxer, som mäts i ljusår. Ett ljusår motsvarar cirka tio biljoner kilometer – ett tal som skulle vara svårt att förstå utan begreppet tiopotenser och utan att omvandla måttenheterna.
Tio potenser är ett praktiskt sätt att uttrycka mycket stora eller mycket små tal. De använder basen 10 och en exponent för att visa hur många gånger 10 multipliceras eller divideras.
Positiva exponenter: En tio potens med en positiv exponent betyder att 10 multipliceras flera gånger med sig själv.
Exempel: betyder 10x10x10=1000.
Negativa exponenter: En tiopotens med en negativ exponent betyder att 10 delas flera gånger.
Exempel: betyder 1/10x10x10=0,001
Tio-potenser gör det enklare att arbeta med mycket stora eller mycket små tal utan att behöva skriva många nollor.
Inom miljöforskningen hjälper stora siffror till att kvantifiera populationer av arter eller mängden molekyler i en viss volym luft, vilket är nödvändigt för att förstå ekosystem och klimatförändringar. Här används ofta siffror i storleksordningen biljoner för att beskriva det enorma antalet naturliga processer.
I nationalekonomin är stora tal också oumbärliga. Beräkningen av ett lands bruttonationalprodukt eller utvärderingen av marknader och deras kapacitet kräver förståelse för och hantering av miljoner, miljarder och biljoner. Dessa tal hjälper ekonomer att analysera och förstå ekonomisk prestanda och trender.

Förmågan att förstå och räkna med stora tal är därför inte bara en akademisk övning, utan en nödvändig färdighet för att hantera komplexa, globala utmaningar inom vetenskap och ekonomi. De hoppar direkt från läroböckerna till verkligheten, där de hjälper oss att mäta, förstå och förvalta vår värld.
Multiplikation med stora tal
När vi arbetar med multiplikation med stora tal är det viktigt att förstå namn på stora tal och hur man hanterar dem. Exempelvis kan vi multiplicera två stora tal som miljarder och biljoner:
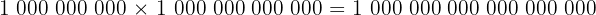
Alltså:

Genom att känna till stora talens namn blir det lättare att läsa och skriva resultat utan att räkna nollor manuellt.
Division med stora tal
Att dividera stora tal kan kännas svårt, men principen är densamma som vid mindre tal. Om vi vill dividera stora tal, exempelvis en biljard med en miljon, kan vi skriva:
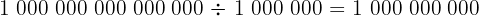
Med andra ord:

Den här typen av övningar besvarar frågan: hur dividerar man stora tal.
De stora talens lag
I sannolikhetsteori talar man om de stora talens lag eller lagen om stora tal. Den säger att om vi upprepar ett slumpmässigt försök många gånger, kommer det genomsnittliga utfallet närma sig det förväntade värdet.
Exempelvis: Om vi kastar en tärning 1 000 000 gånger (ett stort tal!) kommer genomsnittet av alla kast närma sig:
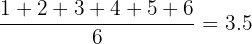
Denna princip är användbar både i statistik och när man arbetar med stora tal i praktiska situationer.
Här kan du läsa mer om skriftlig räknemetod.
Vanliga misstag och missförstånd
När man hanterar stora siffror uppstår ofta misstag och missförstånd som bör undvikas. Ett klassiskt misstag är att förbise betydelsen av decimaler och siffror. Till exempel ignoreras ofta hur betydelsefull en enda siffra kan vara i ett stort tal, särskilt när det handlar om miljarder eller biljoner. Ett annat missförstånd är att blanda ihop metriska prefix, som ”Mio” för miljon och ”Bio” för biljon, vilket kan leda till betydande feltolkningar.
För att undvika sådana misstag är det viktigt att förstå principerna för platsvärdetabellen och tillämpa dem konsekvent. Att grundligt lära sig och regelbundet öva på att förstå stora tal kan hjälpa till att minimera dessa misstag. Om du letar efter stöd lokalt kan du till exempel hitta en lärare matematik stockholm. Dessutom bör elever och studenter tränas i att noggrant kontrollera betydelsen av varje siffra i ett stort tal och att använda metriska prefix korrekt.
Sammanfatta med AI:















