Textuppgifter är en central del av matematikundervisningen och utgör ofta en utmaning för elever i alla årskurser. Aritmetik definition kan beskrivas som läran om tal och de grundläggande räknesätten: addition, subtraktion, multiplikation och division. Att lösa textuppgifter kräver inte bara räknefärdighet, utan också förståelse för vad aritmetik betyder i praktiken – förmågan att extrahera och tillämpa relevant information från texter.
Erfarna aritmetiker utvecklar en systematisk approach och strategiskt tänkande genom övning. I den här artikeln presenterar vi metoder och tips som hjälper dig lösa textuppgifter mer effektivt, från grundläggande strategier för yngre elever till mer avancerade metoder för äldre elever.
Genom att gå igenom exempel och peka på vanliga felkällor vill vi ge eleverna verktyg för att med självförtroende och kompetens kunna lösa matematiska textuppgifter och utöka sin matematiska allmänbildning.
Så här löser du textuppgifter på bästa sätt:
- Läs uppgiften
- Markera nyckelord och viktiga siffror
- Strukturera informationen
- Formulera ekvationen
- (Visualisera problemet)
- Utför beräkningen
- Kontrollera resultatet
Vad är textuppgifter och varför används de?
Textuppgifter, som ofta kallas sakuppgifter i grundskolan, är matematikuppgifter som presenteras i form av texter. De kräver mer än bara tillämpning av räkneoperationer; eleverna måste förstå texten, filtrera ut relevant information och på grundval av detta utveckla en matematisk lösning.
Till skillnad från rena räkneuppgifter, där siffror och ekvationer står i fokus, speglar textuppgifter verkliga problem och kräver tillämpning av matematik i praktiska situationer.
För mig låter matematik alltid så här: ”Två guldfiskar vandrar genom öknen. Den ena är röd, den andra tunn. Hur mycket väger palmen när det regnar?”
Huvudsyftet med textuppgifter är att främja problemlösningsförmågan. De hjälper eleverna att utveckla kritiskt tänkande och analytiska färdigheter genom att lära sig att avkoda komplex information och översätta den till matematiska ekvationer. Textaufgaben tränar förståelsen av matematiska begrepp och förbereder eleverna på att tillämpa dessa kunskaper i vardagliga situationer, till exempel vid beräkning av kostnader, tidsplanering eller inom ramen för vetenskapliga projekt.
Genom att integrera dessa uppgifter i matematikundervisningen uppmuntras eleverna att tänka bortom enkel räkning och se matematik som ett användbart verktyg för olika utmaningar i livet.
Tips för att lösa textuppgifter
Att lösa textuppgifter kan ofta vara svårt för elever. Med en systematisk approach och rätt tekniker kan dock även komplexa textuppgifter hanteras effektivt. Behöver du extra stöd kan du få mattehjälp av en privatlärare.
Steg-för-steg-guide till systematisk lösning:
Läs uppgiften noggrant: Ta dig tid att läsa textuppgiften noggrant. Försök att förstå kärnan i uppgiften och vad som exakt efterfrågas. Detta är det första steget för att säkerställa att du har förstått all nödvändig information.
Markera nyckelord och siffror: Identifiera och markera alla viktiga siffror och nyckelord i texten som indikerar vilka matematiska operationer som krävs. Ord som ”tillsammans”, ”ta bort”, ”mer än” eller ”kvar” kan ge information om du måste additionera, subtrahera, multiplicera eller dividera.
Strukturera informationen: Skriv ner vad som är givet och vad som efterfrågas. Att göra en lista med givna data och den efterfrågade lösningen hjälper dig att strukturera uppgiften.
Formulera ekvationen: Baserat på den insamlade informationen formulerar du en eller flera ekvationer. Detta steg är avgörande, eftersom det översätter dina tankar från texten till matematikens språk.
Visualisera problem: Ibland kan det vara till hjälp att skapa ett diagram, en ritning eller en tabell för att bättre visualisera problemet och förstå relationen mellan uppgifterna.
Utför beräkningen: Lös ekvationerna genom att skriva ut beräkningarna med den markerade informationen. Var noga med att utföra varje beräkningssteg noggrant för att undvika fel.
Kontrollera resultatet: När du har hittat ett svar, läs igenom uppgiften igen och kontrollera att ditt resultat är meningsfullt och korrekt. Se till att du har besvarat alla delar av frågan.
Övning är nyckeln till att bemästra textuppgifter. Använd övningar från din matematikbok eller online-resurser för att vässa dina färdigheter. Regelbunden användning av dessa tekniker kommer att förbättra din förståelse och din förmåga att lösa textuppgifter avsevärt.
Räkneexempel för olika årskurser
Grundskola (årskurs 2):
Addition och subtraktion
Uppgift 1: Tim har 5 euro och hittar ytterligare 3 euro på lekplatsen. Hur mycket pengar har Tim nu?
- Beräkning: 5 euro + 3 euro = 8 euro
- Svar: Tim har nu 8 euro.
Uppgift 2: Anna har 8 godisar. Hon ger sin kompis 3 godisar. Hur många godisar har Anna kvar?
Svar: Anna har nu 5 godisar kvar.
Beräkning: 8 godisar- 3 godisar= 5 godisar
Mellanstadiet (årskurs 5 och 6):
Multiplikation, division, omräkning av enheter och enkla bråk
Uppgift 3: En klass med 24 elever planerar en utflykt. Varje barn får ta med sig 500 ml vatten. Hur många liter vatten blir det totalt?
- Beräkning: 24 barn × 500 ml = 12000 ml = 12 liter
- Svar: Eleverna tar med sig totalt 12 liter vatten.
Uppgift 4: På en bondgård fördelas 56 äpplen jämnt på 8 lådor. Hur många äpplen kommer i varje låda?
- Beräkning: 56 äpplen ÷ 8 lådor = 7 äpplen per låda
- Svar: Det får plats 7 äpplen i varje låda.
Högstadiet (från årskurs 7):
Kombination av olika matematiska operationer, tillämpning av procentberäkning och geometri
Uppgift 5: En rektangulär åker har en längd på 150 meter och en bredd på 80 meter. En staket ska omge hela åkern. Hur många meter staket behövs?
- Beräkning: (150 m + 80 m) × 2 = 460 m
- Svar: Det behövs 460 meter staket.
Uppgift 6: En butik säljer en cykel som ursprungligen kostar 400 euro med 15 % rabatt. Hur mycket kostar cykeln efter rabatten?
- Beräkning: 400 euro × 15 % = 60 euro; 400 euro - 60 euro = 340 euro
- Svar: Cykeln kostar 340 euro efter rabatten.
Klass 8 och 9:
Procentberäkning, treledad regel och indirekt proportionalitet
Uppgift 7: Ett fartyg har tillräckligt med proviant för 40 dagar för en besättning på 15 personer.
Del a: Hur många dagar räcker provianten om det bara finns 8 besättningsmedlemmar ombord?
- Beräkning:
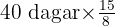personer = 75 dagar - Svar: Förråden räcker i 75 dagar om det bara finns 8 personer ombord.
Del b: Hur många personer räcker förråden till om fartyget ska vara ute i 30 dagar?
- Beräkning:
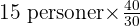Dagar = 20 personer - Svar: Förråden räcker till 20 personer om fartyget är ute i 30 dagar.
Del c: Hur många dagar räcker förråden om 5 män och 1 kvinna går ombord efter 28 dagar, varvid kvinnan förbrukar en tredjedel mindre proviant per dag än en man?
- Beräkning: Total förbrukning per dag efter 28 dagar:
= 
, återstående förråd: 12 dagar x 15 personer = 180 persondagar; ny varaktighet: 
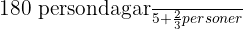= 31,7 dagar. - Svar: Fartyget kan stanna kvar till havs i ytterligare cirka 32 dagar efter de första 28 dagarna.
Uppgift 8: Malte och Nele har samlat 4 kg färska svampar som består av 95 % vatten och 5 % torrsubstans.
Del a: Hur många kilo vatten och torrsubstans innehåller de 4 kg färska svamparna?
- Beräkning: Vatten: 4 kg × 95 % = 3,8 kg; torrsubstans: 4 kg × 5 % =0,2 kg
- Svar: De färska svamparna innehåller 3,8 kg vatten och 0,2 kg torrsubstans.
Del b: Hur många kilo vatten och torrsubstans innehåller dessa svampar efter torkning, om de bara består av 80 % vatten?
- Beräkning: Ny vattenmassa, som motsvarar 80 % av den totala massan efter torkning. Torrmassan förblir 0,2 kg, dvs. total massa x 80 % = = 1 kg, vatten: 1 kg - 0,2 kg = 0,8 kg
- Svar: Efter torkningen innehåller svamparna 0,8 kg vatten och 0,2 kg torrmassa.
Del c: Hur många procent av svampmassan går förlorad vid torkningen?
Beräkning: Massförlust: 4 kg - 1 kg = 3 kg; procentuell förlust: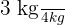 
x 100 % =75 %
Svar: 75 % av svampmassan går förlorad vid torkningen.
Dessa exempel illustrerar hur matematikuppgifter varierar beroende på klassnivå för att främja barnens växande förståelse och förmågor. I grundskolan ligger fokus på grundläggande förståelse för siffror och enkla räknesätt. I mellanstadiet blir uppgifterna mer komplexa med introduktionen av måttenheter, stora siffror och förhållanden, medan man i högstadiet tränar på att använda avancerade räknesätt och lösa problem som kräver flera steg. För elever som bor i huvudstaden kan mattehjälp stockholm vara ett bra komplement till undervisningen.
Vanliga fel och missförstånd
När man löser text- och sakuppgifter i matematik uppstår ofta typiska fel, som oftast beror på missförstånd av texten eller de matematiska metoderna. Ett vanligt fel är att överse viktig information i texten, vilket ofta händer när eleverna inte läser uppgiften noggrant. För att undvika detta är det viktigt att läsa igenom texten flera gånger noggrant och markera nyckelord och siffror som är avgörande för att lösa uppgiften.
Det kan dock också hända att mer information och siffror än nödvändigt medvetet har inkluderats i textuppgiften. Därför bör man alltid fråga sig: ”Vad är det som efterfrågas?” och ”Vad är det som ges?”, för att endast markera den information som är relevant för uppgiften.
Ett annat misstag är felaktig användning av matematiska operationer. Eleverna kan undvika detta genom att kontrollera varje steg i beräkningen och fråga sig om den valda operationen verkligen leder till önskat resultat. Regelbunden övning av matematikuppgifter och deltagande i övningar som fördjupar förståelsen är här oumbärligt.
För att minimera fel bör resultatet granskas kritiskt efter varje löst uppgift. Se till att svaret är logiskt och att det är meningsfullt i uppgiftens sammanhang. Detta steg hjälper inte bara till att upptäcka fel, utan främjar också en djupare förståelse för de matematiska begreppen bakom uppgifterna.
Läs mer om skriftlig aritmetik gjord enkel.
Sammanfatta med AI:
Tycker du om artikeln? Visa det gärna!
Loading...
