De flesta som går grundskolan får en introduktion till det gamla Egyptens fantastiska värld genom roliga lektioner i matematik och historia om Egyptens siffror hieratiska symboler, hieroglyfer och egyptisk konst. Även om vi alla är bekantade med kända ämnen som faraoner och gudomliga symboler - har många av oss glömt hur matematik och vetenskap genom historien har löst problem i många delar av världen.
Visste du till exempel att den beryktade Pythagoras-satsen faktiskt inte upptäcktes av den grekiske matematikern Pythagoras, utan faktiskt redan var etablerad av den så kallade egyptiska triangeln? Om du är intresserad av att lära dig mer om denna stora civilisation så läs vidare - Superprof undersöker allt från antika siffror till Rhindpapyrus!
Här kan du läsa mer om matematikens historia!

De egyptiska tecken, symboler, siffrornas och matematikens historia
Denna ökända civilisation är välkänd för sina fantastiska monument, sin viktiga roll i historien och, kanske framför allt, sin otroliga inverkan på den matematik som vi använder idag. Hur upptäckte vardagliga egyptier så komplexa siffror och formler? Hur uppfanns Egyptens talsystem? Det har en enkel förklaring, de började med att försöka lösa ett problem i sin vardag!
Tänk på de stora pyramiderna i Giza - det är nog inte förvånande nyheter för någon att för att kunna bygga så fantastiska monument som dessa måste denna civilisation ha varit duktiga ingenjörer. Även om de också hade stora färdigheter inom medicin är det upptäckterna inom matematiken som fortfarande används idag.
Komplex matematik och symboler, som det beryktade hieratiska kursivsystemet, kom inte från ingenstans. Det fanns många praktiska problem som behövde lösas för en civilisation av denna storlek. Kan du komma på ett problem som kan ha besvärat hela eller delar av detta forntida land? Här är bara några:
- Översvämningar av Nilen som förstör grödor och landgränser.
- Stora administrativa ansvarsområden på grund av komplexa skattesystem.
- Behovet av att förenhetliga register
- Uppfinningen av ett system för att räkna och registrera transaktioner i ett stort handelssystem.
Även om ett eller flera av dessa problem är något som vi är vana vid att inte behöva hantera varje dag - kom ihåg att detta var ett av de första tillfällen då människor var tvungna att besvara några av dessa svårigheter.
Låt oss ta en titt på hur matematikens historia i Egypten och hur egyptierna vände sina hinder till lösningar som vi fortfarande använder idag! När du får matte hjälp kanske du rent ut av använder dessa metoder och lösningar utan att ens veta det.

Det egyptiska talsystemets symboler
För att förstå hur detta samhälle skapade system för att räkna och utföra operationer bör vi först lära känna vårt eget moderna matematiska system. Skulle du kunna gissa vilken typ av system vi har för att räkna?
Vårt matematiska system kommer faktiskt från babylonierna och kallas för positionssystemet. Det låter komplicerat, men är faktiskt ganska enkelt - vilket är anledningen till att det spreds till många delar av världen och att det fortfarande används idag. De antika Sumererna hade också en väl utvecklad matematik.
Även om vi kanske inte tänker på dem som sådana är våra siffror, som kallas hindu-arabiska siffror, egentligen bara symboler. Vi har sammanlagt 10 av dessa symboler: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. I positionella system skrivs varje symbol beroende på hur de står i förhållande till varandra. För att till exempel skriva talet tio måste vi skriva det i en viss ordning: 10 i stället för 01.
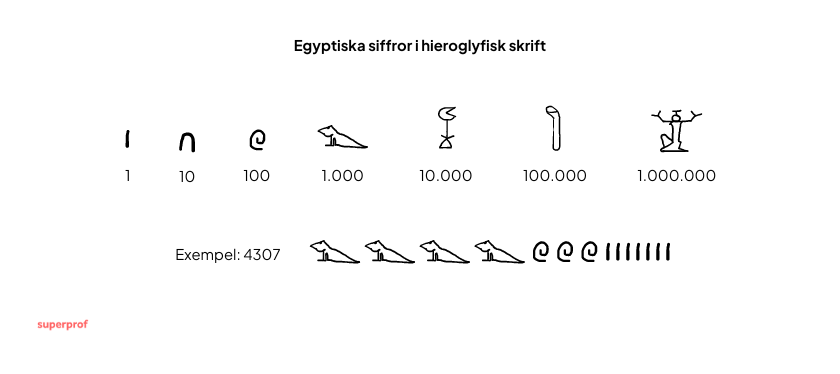
Precis som vi idag använde egyptierna ett decimalsystem. De hade en separat symbol för varje tiopotens från 1 till 1.000.000. Men till skillnad från de siffror vi använder idag hade den egyptiska matematiken inga andra siffror.
För att representera alla andra värden radades flera symboler upp och adderades. Det var alltså inte ett positionssystem, utan ett additivt system. För att skriva talet 328, till exempel, måste symbolen för 100 skrivas tre gånger, symbolen för 10 två gånger och symbolen för 1 åtta gånger.
Medan symbolen för 1 i hieroglyferna är en enkel linje och 10 bara är en nedåtriktad båge, blir symbolerna mer och mer komplexa i takt med att kraften ökar. Värdet 1.000.000 representeras av den ganska komplexa hieroglyfen för Heh, den egyptiska oändlighetens gud. I dagligt bruk är det ganska komplicerat och förvirrande att skriva och läsa ett additivt talsystem. Senast i hundratal kan värdena knappast identifieras med en blick. Det måste räknas om varje gång.
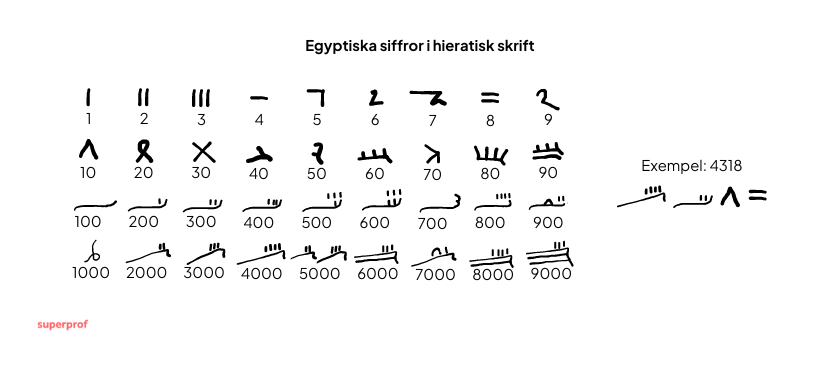
Därför skrevs siffrorna med den enklare hieratiska skriften från omkring det 3:e årtusendet f.Kr. Hieratisk sifferskrift består av totalt 36 tecken, som kan användas för att representera siffrorna från 1 till 9 999 i en förenklad form. De enskilda värdena adderas fortfarande för att få det totala numeriska värdet.
Ett forntida folk som inte använde sig av ett positionssystem var kineserna! Deras system är ett utmärkt exempel på ett gammalt, icke-positionellt siffersystem. Lär dig mer om forntida kinesisk matematik här!

Rhindpapyrus
Även om vi känner till den matematik och de operationer som de antika egyptierna använde sig av, vet vi faktiskt inte mycket om hur de kom fram till alla dessa stora upptäckter. Detta beror på att även om vi har en del bra uppteckningar om vad berömda hieratiska symboler betydde eller betydelsen av det egyptiska ögat, så finns inte många uppteckningar om de delar av matematiken som de stora egyptierna skapade bevarat.
En del av problemet är förstås hur gamla dessa uppteckningar är, men delar av stora samlingar av uppteckningar och matematiska texter tros också ha brunnit under den stora branden i biblioteket i Alexandria.
Ett undantag är det som kallas Rhindpapyrus. Detta dokument, som upptäcktes av den skotska egyptologen Henry Rhind på 1800-talet, är en av de enda matematiska texter vi har från det gamla Egypten. Rhindpapyrus innehåller 84-87 beräkningar som användes för att hjälpa vanliga människor i deras dagliga liv.
Matte är ett komplext ämne att lära sig och ofta har man antingen väldigt lätt för att förstå det, eller så är det en enorm utmaning att se logiken. Kanske matematik undervisning online är precis det du behöver för att lära dig matte?

Dessa problem varierade från komplexa till triviala. Ett exempel på ett enkelt problem var h att dela antalet bröd, n, mellan 10 personer. Problem nummer 1 löste denna ekvation när n var lika med 1 bröd. Problem 2 var när n = 2 bröd, problem 3 för n = 6 bröd osv.
Ta hjälp av läxhjälp matematik Stockholm för att förstå bättre.
Komplexa hieroglyfiska bråk och formler
En annan sak som ingick i Rhind-papyrusen? Bråktalen och en metod för att räkna dem. Med ett undantag använde de forntida egyptierna bara vanliga bråktal, som de strängade ihop för att få ett exakt värde. Vanliga bråktal är bråktal med 1 i täljaren, t.ex. 1/2, 1/5 eller 1/360. 2/3 är det enda bråktal utan 1 i täljaren som har en egen symbol.
För att representera andra bråktal måste de delas upp i rotfraktioner. Bråktalet 3/5 består av 1/2 + 1/10. Uppdelningen är dock inte alltid tydlig. Till exempel kan bråket 7/8 brytas ned till 1/2 + 1/3 + 1/24 men också till 1/2 + 1/3 + 1/30 + 1/120. Intressant nog skulle egyptierna förmodligen ha valt den andra notationen, eftersom nämnaren om möjligt bör vara en divisor av 60, 360 eller 3600.
Bråken skrevs med siffrorna från den hieroglyfiska skrift som presenterades ovan i nämnaren samt en oval ovanför (hieroglyf för mun). För bråket 2/3 lades två vertikala linjer till längst ner på ovalen.
Har du förresten koll på Mayafolkets talsystem?
Den egyptiska triangeln
En sak som du kanske inte visste om denna civilisation är att de faktiskt uppfann något som du kanske känner till. Låt oss spela ett spel! Kan du gissa vad dessa människor uppfann? Här är några ledtrådar:
- Den är formad som en triangel.
- Du kan använda den här formeln för att hitta avstånden mellan vinklarna.
- Många människor tror att grekerna är ansvariga för denna uppfinning.
Har du en gissning? Egyptierna har faktiskt gjort en approximation av det som du känner till som Pythagoras sats! Pythagoras sats uppfanns omkring 500 f.Kr. och man vet faktiskt inte mycket om huruvida denna sats var välkänd vid den tiden.
För att kunna bygga alla de otroliga pyramider och strukturer som egyptierna gjorde är det dock välkänt att de använde det som kallas 3:4:5-triangeln dagligen och i praktiken. Med andra ord var dessa människor otroligt begåvade ingenjörer.
Triangeln 3:4:5 är en rätvinklig triangel. Tricket med denna triangel är att oavsett vilka enheter du mäter i - meter, kilometer osv. - ska du alltid göra triangeln med förhållandet 3:4:5.
Här är de motsvarande sidorna till detta förhållande. Du kanske redan vet detta om du är bekant med Pythagoras sats. Kämpar du med att förstå Pythagoras sats kan du boka lektioner i matte online och be en privatlärare förklara mer ingående.
Det fina med denna "magiska" form är att varje sida var ett helt tal. Detta var bra eftersom det, som vi har sett, ofta fanns många problem med att räkna och utföra beräkningar med egyptiska siffror.
Här hittar du en genomgående guide till romerska tal och siffror.

Det fina med denna triangel är att det är en rätvinklig triangel. Högertrianglar är mycket speciella inom matematiken eftersom de har riktigt bra egenskaper. En sådan egenskap är att varje annan vinkel än 90-gradersvinkeln är en komplementär vinkel. Om du har en rätvinklig triangel kan du alltid räkna ut de andra två vinklarnas vinklar så länge du har 1 vinkelstorlek och två sidlängder av triangeln.
Det är välkänt att egyptierna faktiskt använde rep för att mäta trianglarnas vinklar. De gjorde det genom att skapa 12 knutar i ett rep.
Nu har vi tittat närmre på Egyptens siffror, hieratiska symboler, hieroglyfer och egyptisk konst och framförallt deras tidiga matematik. Även om vi alla är bekantade med kända ämnen som faraoner och gudomliga symboler sedan tidigare - är det lätt att glömma hur matematik och vetenskap genom historien har löst problem i många delar av världen. Vi är och har varit beroende av matematiken för att komma fram till nya upptäckter.
Nu vet du också att den beryktade Pythagoras-satsen faktiskt inte upptäcktes av den grekiske matematikern Pythagoras, utan faktiskt redan var etablerad av den så kallade egyptiska triangeln. Ett annat antikt folk som var tidiga med uträkningen som vi döpt efter Pythagoras är Sumererna, vilket har hittats nedskrivet på två babyloniska tavlor som visar en lista över Pythagoras sats.
Sammanfatta med AI:















