Vad är sexagesimalt och vad exakt är kilskrift? Även om det finns många ikoniska bilder och historiska ögonblick som vi känner till från en annan gammal matematisk jätte, egyptierna, har många människor svårt att komma ihåg vad babylonierna gick för.
Om du någonsin har tagit en matematikkurs eller fått matte hjälp där läraren talat om Mesopotamien, så har du lärt dig om babylonierna. Babylon, som ligger i dagens Iran och Irak, brukar många tänka på som en av de första stora städerna. Även om detta kan diskuteras kan vi inte förneka den inverkan som den babyloniska civilisationen har haft på dagens politik, historia och matematik.
Du kan använda dina kunskaper om babyloniska siffror för att förstå vår matematik i dagens värld. Att lära sig om sexagesimal- och kilskriftsnotationen kan hjälpa dig att besvara frågor som du inte ens visste att du hade om vårt eget räknesystem. Till exempel, varför är nollan i mitten av alla tal?
Är du nyfiken på Mayafolkets talsystem så kan du läsa om det här. Men för nu, låt oss dyka in i denna forntida civilisations matematiska historia och lära oss om babyloniernas talsystem!

Den babyloniska civilisationens historia
Mesopotamien var en region i antikens historia som omfattade delar av dagens Turkiet, Syrien, Iran, Irak och Kuwait - och som sträcker sig längs med flodsystemen Tigris och Eufrat. Du kanske också har hört talas om denna region som kallas den bördiga halvmånen.
Även om deras matematiska system verkar helt annorlunda än våra egna, ledde Mesopotamiens och Egyptens talsystem till födelsen av den matematik som vi känner till i dag. Går du en historiekurs kan du lära dig att den mesopotamiska civilisationen började omkring 3100 f.Kr. och slutade med Babylons fall 539 f.Kr.
De människor som bebodde regionen kallas ofta för babylonier, även om de i verkligheten kallas sumerer och akkadier. Mycket av det som dessa forntida människor upptäckte skrevs ner på lertavlor. De lertavlorna ger oss idag en hel del insikt i den typ av problem som de var tvungna att lösa dagligen.
I likhet med annan forntida matematik, till exempel kinesisk matematik, är mycket av det som upptäcktes i Mesopotamien sådant som vi i dag betraktar som ganska grundläggande matematik. På dessa babyloniska tavlor hittar du idéer som kvadratiska och kubiska ekvationer och Pythagoras sats! Låt oss ta en närmare titt på deras matematiska notationer och siffror.

Det babyloniska talsystemet - ett positionellt talsystem
För att förstå det babyloniska talsystem som dessa människor använder, måste vi först förstå vårt eget talsystem. I modern tid använder vi ett positionellt talsystem. Även om detta kanske redan låter som en komplicerad matematisk term är det egentligen ganska enkelt.
Positionella tal är helt enkelt siffrorna noll till nio. Även om vi bara har dessa 10 symboler (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) är vi inte bara begränsade till att göra nummer 9 och lägre. Vi kan använda dessa symboler i kombinationer för att skapa miljontals andra olika tal.
Dessa siffror skrivs och läses också från vänster till höger i en kolumn. Beroende på var siffran är placerad motsvarar den ett visst belopp. Låt oss ta en titt på vad detta betyder!
Som du kan se är det mycket viktigt var vi placerar 2:an eftersom den kan innebära att vi antingen har 20 eller 200. Vi kan inte placera 2:an i mitten, som 020, och läsa det som 200. Detta är vad ett positionellt talsystem innebär.
Det första babyloniska talsystemet var däremot inte det positionella systemet. Om vi går tillbaka till omkring 3500 f.Kr. ser vi att sumerierna använde ett matematiskt system där notationen för tal var olika symboler.
Sumererna hade endast symboler för siffrorna 1, 10, 100 och 1000. Detta innebär att de bara kunde skriva upp till siffran 9999.
Liksom många andra forntida civilisationer, inklusive det romerska talsystemet, hade de ingen symbol för nollan. Symbolen för 1 var en ficklampa, symbolen för 10 var en pil osv. Det spelade egentligen ingen roll i vilken ordning man skrev dessa symboler, eftersom varje tal hade sin symbol. Detta innebär att det var icke-positionellt.
Detta system hade många brister. Så vid en tidpunkt i deras historia gjorde de flera reformer av sitt numeriska system. Först antog de det positionella system som vi använder i dag. Men i stället för att ha en bas på 10 som vi gör idag använde dessa människor faktiskt ett matematiskt system med en bas på 60.
Ett specialord för talsystem med en bas på 60 är ett sexagesimalt talsystem. Från deras sexagesimalsystem med basen 60 kommer faktiskt vår moderna användning av olika saker som 60 sekunder i en minut, 360 grader i en cirkel och mycket mer!
Detta innebär att de hade symboler för varje tal mellan 1 och 59. Eftersom det var positionellt betyder det att om du hade en symbol för 1 och 40 på samma sätt skulle du få:
1*60 + 40*60 = 2460
Talet 60 var ett bra tal att välja som bas eftersom det gjorde bråkbildningar superlätt eftersom 60 har många faktorer eller tal som det kan delas med. Det är bara att jämföra faktorerna för dessa två olika baser.
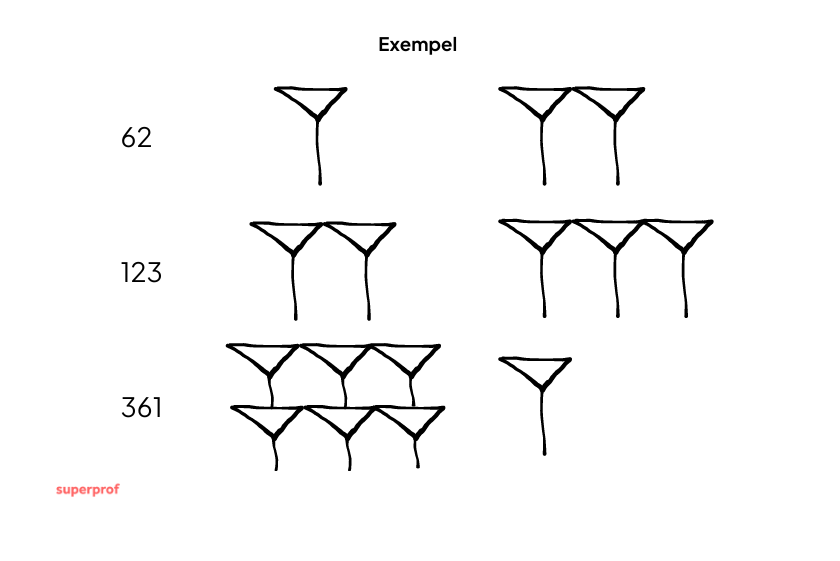

Matematik på antika lertavlor
Till skillnad från den egyptiska matematiken, där vi har mycket få uppgifter kvar om deras matematiska processer, har vi massor av information om sumerisk matematik. Medan egyptierna skrev sina numeriska processer och system på papyrus skrev den sumeriska civilisationen ner sina uppgifter på lertavlor.
Dessa forntida folks olika bråk och notationer skrevs på leran när leran fortfarande var våt. Dessa tavlor bakades sedan antingen i en ugn eller lämnades helt enkelt att torka i solens värme. Lyckligtvis har forskare kunnat återfinna omkring 400 av dessa tavlor. De flesta av dessa kommer från den så kallade gammalbabyloniska perioden, som sträckte sig från 1830 till 1531 f.Kr.
Dessa människor skrev på leran i en typ av skrift som kallas kilskrift. Kilskrift brukar beskrivas som kilformad och är - tillsammans med egyptiska hieroglyfer - ett av de tidigaste skriftsystemen i världen.
Du kanske märker att kilskrift skiljer sig mycket från de egyptiska hieroglyferna. Den kilformiga skriften uppstod faktiskt på grund av att dessa tidiga människor inte kunde skapa böjda linjer inuti leran på ett enkelt sätt.
Vi har hittat många principer för matematik skrivna på dessa tavlor. Dessa matematiska nerteckningar inkluderar teman som: bråk, kvadratiska och kubiska uttryck och till och med Pythagoras sats!
Matte kan vara klurigt att lära sig, inte minst när vi dessutom talar om komplicerade modeller och principer. Som tur är finns det mattehjälp online som skapar en individanpassad studieupplevelse! Kanske det är något för dig?

Babylonisk tabell över kvadrater
Även om du kanske är van vid att räkna ut kvadrater lätt, eftersom du kanske har varit tvungen att memorera dem i skolan, hade dessa forntida människor det inte lika lätt som vi har det i modern tid. Eftersom sumererna hade lite mer komplexa symboler och regler för sitt talsystem var de tvungna att hitta en bättre lösning.
Eftersom det babyloniska talsystemet hade en bas 60 kunde det vara svårt att beräkna vissa av de tal som vi anser vara superenkla i dag. Dessutom fanns det inga decimaler i deras system - bara heltal (även kallade hela tal). Kvadrattabellen var ett sätt att skriva ner riktlinjerna för några av de operationer som skulle ha varit lite knepiga att bara memorera.
Matematikens värld är enorm, och du kommer aldrig få slut på saker att lära dig och utvecklas inom. Ta mattehjälp för att navigera de formler och problem just du behöver.
Mayafolkets talsystem var marginellt enklare, med en bas på 20.
År 1877 analyserades två tavlor av tysken Richard Lepsius. Dessa två tavlor, beskrev han, var faktiskt listor, eller tabeller, av kvadrater. Denna analys och slutsats bekräftades också av George Rawlinson och George Smith. Denna tabell med kvadrater gav många insikter om hur sumererna utförde matematik.
Pythagoras tripplar
Det var inte bara det gamla Grekland och Egypten som kom fram till något som ligger nära det vi känner till som Pythagoras sats, utan även de gamla babylonierna upptäckte denna något magiska triangel. Två babyloniska tavlor har upptäckts som visar en lista över Pythagoras triplar.
Dessa tavlor är daterade till cirka 1 000 år innan Pythagoras faktiskt levde, vilket tyder på att den beryktade satsen faktiskt inte först upptäcktes av den grekiske matematikern och filosofen.
De upptäckta tavlorna, varav en är viktigare för denna triangelsats, kallas Si.427. Den visar hur man använder pythagoriska triplar för att skapa räta vinklar. Du kanske undrar varför detta är så viktigt?
Rätta trianglar inom ingenjörsyrket, särskilt förr i tiden - och vi pratar långt tillbaka - var oerhört viktiga för att bygga stora strukturer, kartlägga landområden och ännu mer. Pythagoras tripplar kunde därför användas för att rita bättre kartor.
Om du tar en titt på själva tavlan kanske den inte ser ut som mycket. Men vad du kommer att se är kilskrift tillsammans med många vinkelräta linjer. Detta var för att exakt kunna beräkna den rätta vinkeln.
Som du säkert förstått så har sumerisk matematik och det babyloniska talsystemet spelat stor roll både för dem men även för oss idag. Vår moderna matematik har anrika grunder som kommer från forntida folk, inte bara grekerna, vilket det kan vara lätt att tro när vi kallar det för "Pythagoras sats" till exempel. Vill du veta mer om matematikens historia vill jag tipsa om denna artikel.
Kul att du intresserar dig för matematik!
Sammanfatta med AI:















