Matteregler är de grundläggande regler och principer som styr hur matematiska operationer och koncept fungerar. Dessa regler används för att utföra beräkningar, lösa problem och bevisa teorem inom matematiken.
Matteregler utgör grunden för matematisk förståelse och tillämpning och är oumbärliga verktyg för att arbeta med olika typer av matematiska problem. De kan omfatta allt från enkla räkneregler till mer avancerade koncept inom algebra, geometri, sannolikhet och statistik.
I den här artikeln ska vi främst fokusera på de matematik regler som högskoleprovet kommer att ha med.
Matteregler inför högskoleprovet
Att ha en god förståelse för några grundläggande matteregler är avgörande för att lyckas på högskoleprovet i matematik. Några kommer du säkert känna igen, Pythagoras sats och multiplikationstabellen till exempel.
Här är några av de viktigaste mattereglerna som är bra att kunna inför provet:
- Algebraiska regler
- Geometriska regler
- Procentregler
- Sannolikhetsregler
- Statistikregler
- Logaritmer
- Exponentialregler
Att behärska dessa matteregler och kunna tillämpa dem på olika problem är avgörande för att lösa matematikdelen av högskoleprovet på ett effektivt sätt. Oro dig inte, vi ska gå igenom dem i detalj var för sig.
Algebraiska regler
Algebraiska regler är centrala inom algebra och används för att manipulera och förenkla algebraiska uttryck, ekvationer och olikheter.
- Distributiv egenskap: Distributiviteten är en av de grundläggande algebraiska reglerna och säger att multiplikationen distribueras över additionen.
- Exempel:
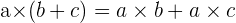
- Detta innebär att om du multiplicerar ett tal eller en variabel med en summa av två termer, multipliceras det med varje term separat och sedan adderas resultaten.
- Exempel:
- Associativ egenskap: Den associativa egenskapen gäller för både addition och multiplikation och säger att ordningen i vilken operationer utförs inte påverkar det slutliga resultatet.
- Exempel:
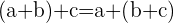
- Detta betyder att du kan gruppera tal eller variabler på olika sätt när du adderar dem och fortfarande få samma resultat.
- Exempel:
- Kommutativ egenskap: Kommutativiteten gäller för både addition och multiplikation och säger att ordningen av termerna inte påverkar det slutliga resultatet.
- Exempel:
- Detta betyder att du kan ändra ordningen på termerna när du adderar dem och fortfarande få samma resultat.
- Exempel:
Vill du skapa bättre förutsättningar för dig själv inför provet? Undersök då möjligheterna som kommer med matematik undervisning online.
- Kvadreringsregeln: Kvadreringsregeln används för att utveckla kvadrerade uttryck.
- Exempel:
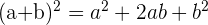
- Detta är en användbar formel för att utveckla kvadratiska uttryck och kan användas för att förenkla och lösa olika typer av algebraiska problem.
- Exempel:
- Kvadratrotregeln: Kvadratrotregeln säger att kvadratroten av ett kvadrerat uttryck är lika med absolutvärdet av det ursprungliga uttrycket.
- Exempel:
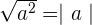
- Detta betyder att när du tar kvadratroten av ett kvadrerat uttryck, måste du beakta både det positiva och det negativa värdet, eftersom kvadratroten av ett negativt tal är komplex.
- Exempel:
Här kan du läsa mer om den matematik som kommer att komma på högskoleprovet.
Geometriska regler
Geometriska regler är grundläggande principer och egenskaper som styr geometriska figurer och deras förhållanden. Dessa regler används för att beräkna längder, områden, volymer och andra egenskaper hos geometriska objekt. Här är några av de viktigaste geometriska reglerna och egenskaperna:
- Pythagoras sats:
- Pythagoras sats är en grundläggande relation i geometrin som gäller för rätvinkliga trianglar. Den säger att summan av kvadraterna på kateterna i en rätvinklig triangel är lika med kvadraten på hypotenusan.
- Formel:
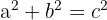, där och är längderna på kateterna och är längden på hypotenusan.
- Areaformler:
- Areaformler används för att beräkna ytan av olika geometriska figurer, såsom kvadrater, rektanglar, trianglar och cirklar.
- Exempel: Area av en kvadrat =
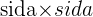, Area av en triangel = 
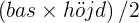, Area av en cirkel = 
- Volymformler:
- Volymformler används för att beräkna volymen av olika tredimensionella geometriska figurer, såsom kuber, rätblock, pyramid, kon, cylinder och sfär.
- Exempel: Volym av en kub =
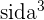, Volym av en cylinder = 
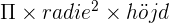, Volym av en kon =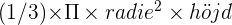 
- Egenskaper hos cirklar:
- En cirkel är en geometrisk figur där alla punkter på omkretsen ligger lika långt från centrum.
- Omkrets: Omkretsen av en cirkel beräknas med formeln
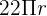, där 
är radien. - Area: Arean av en cirkel beräknas med formeln
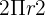, där är radien.
- Egenskaper hos rätvinkliga trianglar:
- Vinkelsumma: I en rätvinklig triangel är summan av de tre vinklarna 180 grader.
- Trigonomiska förhållanden: Förhållandet mellan sidorna och vinklarna i en rätvinklig triangel, såsom sinus, cosinus och tangens.
Det finns matte hjälp att få för den som är i behov av extra stöd och vägledning under studierna. Ge det en chans och upptäck alla fördelarna!
Procentregler
Procentregler är grundläggande regler för att hantera procentuella förändringar och beräkningar inom matematiken. Att förstå och kunna tillämpa dessa regler är viktigt i många sammanhang, inklusive ekonomi, handel, statistik och vardagliga situationer. Här är några av de vanligaste procentreglerna och hur de används:
- Beräkning av procentuellt värde: För att beräkna ett procentuellt värde av en given mängd använder vi formeln:
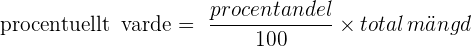
Till exempel, om vi vill räkna ut 25% av 80 kronor, använder vi formeln: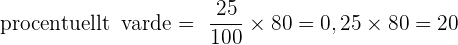
- Procentuella förändringar: För att beräkna procentuell ökning eller minskning använder vi följande formel:
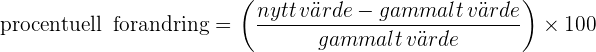
Om ett pris går från 100 kronor till 120 kronor, är procentuell ökning: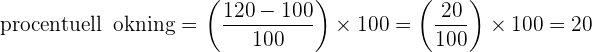
- Att öka eller minska ett värde med en given procent: För att öka eller minska ett värde med en viss procent, använder vi följande formel:
- Öka:
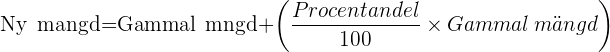
- Minska: Till exempel, om vi ökar 80 kronor med 25%, blir den nya mängden:
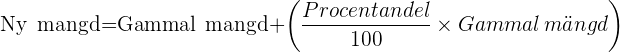
Till exempel, om vi ökar 80 kronor med 25%, blir den nya mängden: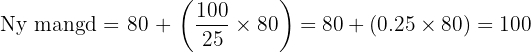
- Öka:
Sannolikhetsregler
Sannolikhetsregler är regler som används för att analysera och beräkna sannolikheter för olika händelser och utfall inom sannolikhetslära. Dessa regler är centrala för att förstå och hantera sannolikhetsproblem, både i vardagen och inom matematiska och statistiska sammanhang.
Vi tipsar om vad du behöver öva på inför högskoleprovet i matematik.
Här är några av de viktigaste sannolikhetsreglerna:
Additionsstatsen
Additionssatsen används för att beräkna sannolikheten för att minst en av två händelser inträffar. Om A och B är två händelser är sannolikheten för att antingen händelse A eller händelse B inträffar 
given av: 
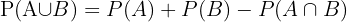där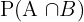 
är sannolikheten för att båda händelserna inträffar samtidigt.
Multiplikationssatsen
Multiplikationssatsen används för att beräkna sannolikheten för att både händelse 
och händelse 
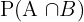inträffar. Om och är oberoende händelser är sannolikheten för att både och inträffar given av: 
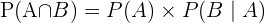där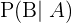 
är sannolikheten för att händelse inträffar givet att händelse redan har inträffat.
Komplementregeln
Komplementregeln används för att beräkna sannolikheten för en händelse och dess komplement (det som inte är händelsen). Om är en händelse är sannolikheten för att händelse inte inträffar 
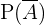given av: 
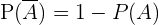där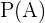 
är sannolikheten för att händelse inträffar.
Total sannolikhetsregel
Total sannolikhetsregel används för att beräkna sannolikheten för en händelse genom att använda villkorsbetingade sannolikheter och partitionerade händelser. Om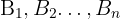 
är en partition av utfallsrummet och är en händelse är sannolikheten för händelse given av: 
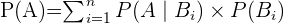där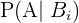 
är sannolikheten för händelse givet att händelse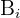 
inträffar, och 
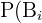är sannolikheten för händelse .
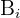Oavsett om matematik är något du har generellt lätt för att förstå, eller om det är något som hängt över dig under alla skolår. Det finns matte hjälp att få där din handledare möter dig på din nivå och hjälper dig öka förståelse för matematiska begrepp, stärka ditt självförtroende och lägga upp en plan för dina studier.
Statistikregler
Statistikregler är de regler och principer som används för att analysera och tolka data inom statistik. Dessa regler hjälper till att förstå och beskriva egenskaper hos datamängder och att dra slutsatser från dem. Här är några av de viktigaste statistikreglerna:
- Medelvärde (genomsnitt):
- Medelvärdet av en datamängd är summan av alla värden dividerat med antalet värden.
- Exempel: Medelvärdet av 5, 10 och 15 är
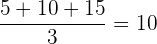
- Median:
- Medianen är det mittersta värdet i en ordnad datamängd. Om antalet värden är jämnt, är medianen det genomsnittliga värdet av de två mittersta värdena.
- Exempel: Medianen av 3, 7, 10, 12, 15 är 10.
- Typvärde (modus):
- Typvärdet är det värde som förekommer mest frekvent i en datamängd.
- Exempel: Typvärdet av 2, 3, 3, 5, 7, 7, 7 är 7.
- Standardavvikelse:
- Standardavvikelsen är ett mått på spridningen av värdena i en datamängd runt medelvärdet. Ju större standardavvikelse, desto mer spridda är värdena från medelvärdet.
- Exempel: Om standardavvikelsen är låg, indikerar det att värdena ligger nära medelvärdet och att datamängden är mindre spridd.
- Kvartiler:
- Kvartilerna delar datamängden i fyra lika stora delar. Kvartil 1 (Q1) är den lägsta 25% av värdena, kvartil 2 (Q2) är medianen och kvartil 3 (Q3) är den högsta 25% av värdena.
- Exempel: Kvartilerna för 10, 15, 20, 25, 30 är Q1 = 15, Q2 = 20, Q3 = 25.
- Histogram:
- Ett histogram är en grafisk representation av frekvensen eller fördelningen av värden i en datamängd. Det visar hur många gånger varje värde eller värdeintervall förekommer.
- Exempel: Ett histogram kan användas för att visa fördelningen av poäng på ett prov.
Detta quiz har vi gjort för att hjälp dig testa vilken nivå du har i matematiken.
Logaritmer
Logaritmer är matematiska funktioner som är inversa till exponentiation. De används för att förenkla och hantera exponentiella uttryck och kan vara användbara för att lösa olika typer av problem inom matematik, naturvetenskap och ingenjörsvetenskap. Här är en mer ingående beskrivning av några vanliga logaritmer regler:
- Logaritmregel för produkter:
- Om vi har två tal och och multiplicerar dem tillsammans, kan vi skriva detta som en summa av deras logaritmer:
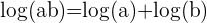
- Detta innebär att logaritmen av en produkt är summan av logaritmen av de enskilda faktorerna.
- Om vi har två tal och och multiplicerar dem tillsammans, kan vi skriva detta som en summa av deras logaritmer:
- Logaritmregel för kvoter:
- Om vi har två tal a och b och dividerar dem, kan vi skriva detta som differensen mellan deras logaritmer:
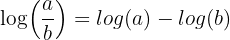
- Detta innebär att logaritmen av en kvot är differensen mellan logaritmen av täljaren och logaritmen av nämnaren.
- Om vi har två tal a och b och dividerar dem, kan vi skriva detta som differensen mellan deras logaritmer:
- Logaritmregel för potenser:
- Om vi har en potens av ett tal a upphöjt till en exponent n, kan vi skriva detta som produkten av exponenten och logaritmen av basen:
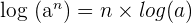
- Detta innebär att logaritmen av ett tal upphöjt till en exponent är exponenten multiplicerad med logaritmen av basen.
- Om vi har en potens av ett tal a upphöjt till en exponent n, kan vi skriva detta som produkten av exponenten och logaritmen av basen:
- Logaritmregel för kvadratroten:
- Om vi har kvadratroten ur ett tal a, kan vi skriva detta som hälften av logaritmen av talet:
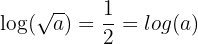
- Detta innebär att logaritmen av kvadratroten ur ett tal är hälften av logaritmen av talet.
- Om vi har kvadratroten ur ett tal a, kan vi skriva detta som hälften av logaritmen av talet:
Exponentialregler
Exponentialregler är regler som styr hur man hanterar exponentiella uttryck och potenser. Dessa regler är användbara för att förenkla och manipulera matematiska uttryck som innehåller exponenter. Här är några av de viktigaste exponentialreglerna:
- Multiplikationsregeln för exponenter: Om man multiplicerar två tal med samma bas, adderas exponenterna.
- Exempel:
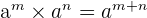
- Detta innebär att om man multiplicerar två tal med samma bas, lägger man helt enkelt ihop exponenterna.
- Exempel:
- Division av exponenter: Om man delar två tal med samma bas, subtraheras exponenterna.
- Exempel:
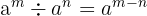
- Detta innebär att om man dividerar två tal med samma bas, subtraherar man exponenterna från varandra.
- Exempel:
- Potensregeln för potenser: Om man har en potens upphöjd till en annan potens, multipliceras exponenterna.
- Exempel:
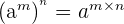
- Detta innebär att om en potens är upphöjd till en annan potens, multipliceras exponenterna med varandra.
- Exempel:
- Negativa exponenter: En negativ exponent betyder att man tar den reciprokta (1/den ursprungliga) av basen upphöjd till den positiva exponenten.
- Exempel:
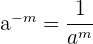
- Detta innebär att om en exponent är negativ, tar man den reciprokta av basen upphöjd till den positiva exponenten.
- Exempel:
- Nollexponenten: En exponent på noll resulterar alltid i 1, så länge basen inte är 0.
- Exempel:
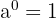(för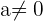 
) - Detta innebär att oavsett vilket värde basen har, kommer en exponent på noll alltid att resultera i 1, så länge basen inte är 0.
- Exempel:
Det finns såklart en hel del mer du behöver lära dig innan du ska skriva högskoleprovet i matematik, men om du lär dig dessa matematikregler är du en god bit på vägen.
Du kan testa hur bar koll du har på matematik med vårat mattetest här.
Tycker du om artikeln? Visa det gärna!
Loading...
