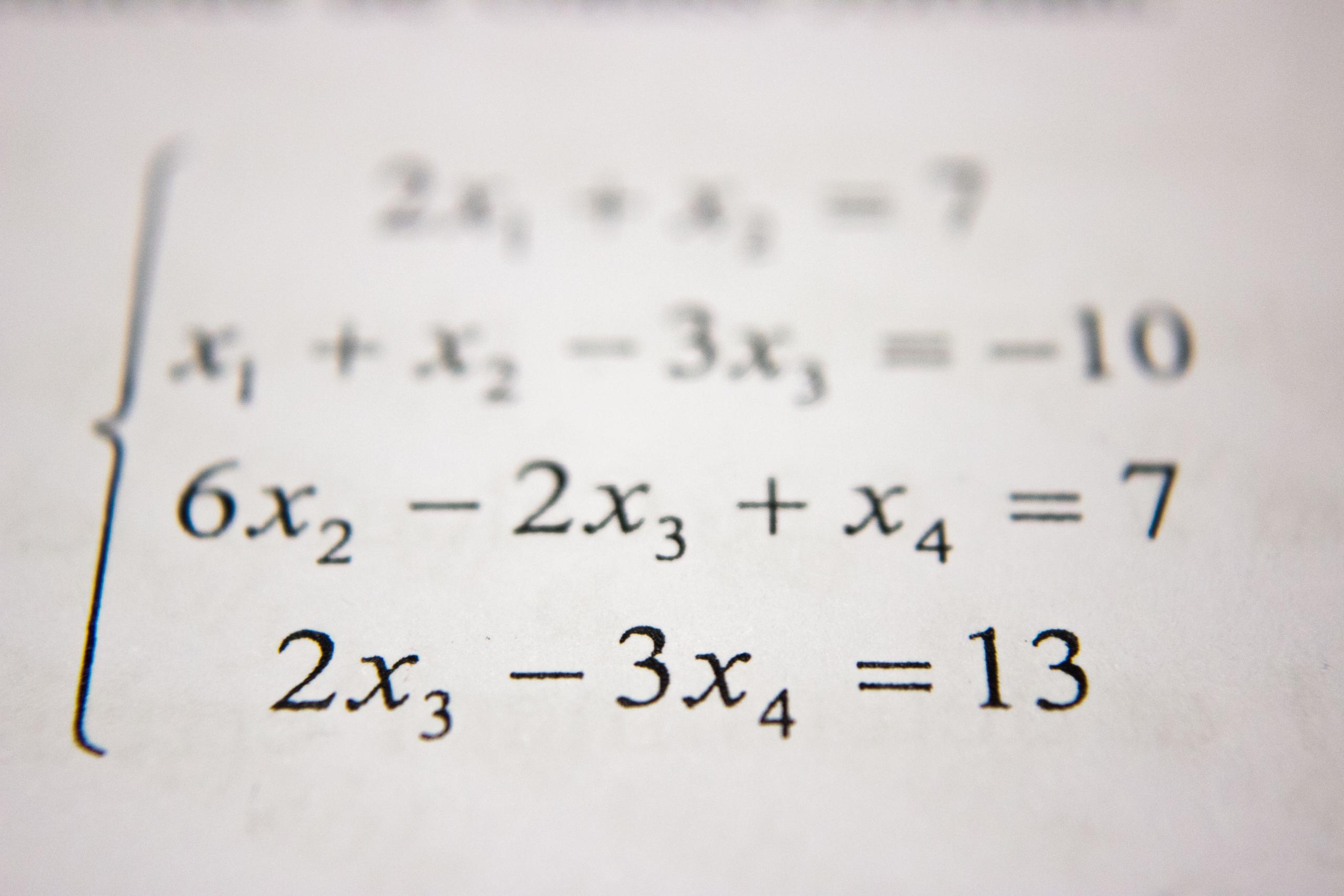Människor har delade åsikter om algebra och dess grunder. Hälften av befolkningen hävdar att algebra är hjälpsamt, medan resten av befolkningen inte kunde bry sig mindre. De individer som älskar algebra uppskattar dess logik och praktiska funktioner, medan andra kritiserar att det sällan kan användas i vardagen.
Finns det någon korrekt åsikt? Hur kan man tänka när det gäller grunderna i algebra?
Även om algebra inte är något för alla så är det en kritisk aspekt av matematiken. Den förtjänar faktiskt att få särskild uppmärksamhet. Genom att lösa olika algebraiska problem kan man förbättra sina förmågor vad gäller problemlösning och kritiskt tänkande, vilket är otroligt värdefullt i vardagen.
De som bekantar sig med algebra öppnar dessutom upp för en hel rad nya karriärmöjligheter! Det beror på att goda algebrakunskaper uppskattas och efterfrågas inom många olika arbetsområden.
I denna artikel ska vi ta en närmare titt på algebrans grunder. Vi berättar även hur du kan gå tillväga för att lära dig algebra. Om du vill titta närmare på olika algebraiska exempel kan du spana in våra andra artiklar om algebra.
Vem vet...kanske får du snart upp ögonen för detta spännande matematiska område.

Vem uppfann algebra?
Algebra är ett viktigt matematiskt koncept som har funnits i många århundraden. Många erfarna matematiker hävdar att den moderna vetenskapens banbrytande upptäckter skulle ha varit omöjliga utan algebrans utveckling.
Så vem är det geni som uppfann de begrepp, regler och ekvationer som är förknippade med algebra?
Algebra härstammar från ordet al-jabr. Detta ord hittades ursprungligen i Muhammad ibn Musa al-Khwarizmis manuskript från 800-talet vars titel kan översättas till "Kompendium om beräkning genom komplettering och balansering".
Al-Khwarizmis bok var ett mästerverk som gav praktiska svar och läsningar när det kom till fördelning av mark, regler för arv och jämn lönefördelning. Termen "al-jabr" kan översättas till "att komplettera" eller "återställa". Termen refererar helt enkelt till den matematiska metod då man tar bort ett negativt tal från den ena sidan och lägger till ett positivt tal på den andra.
Faktum är att Al-Khwarizmi - algebrans fader - var en av sin tids bästa matematiker och astronomer. Även om Al-Khwarizmi tillskrivs de tidigaste teorierna om algebra så var de de europeiska matematikerna som introducerade den symboliska algebra vi använder idag.
Det skedde dock inte förrän under renässansen. Intressant nog utvecklade Al-Khwarizmi också begreppet "algoritm" inom matematiken och ses därför som en tidig pionjär inom datavetenskapen.
Skaffar du matte hjälp kommer du att få lära dig allt du behöver veta om algebra!

Vad är algebra?
Bävar du inför din nästa matematiklektion? Verkar de algebraiska problemen helt omöjliga att lösa? Ifrågasätter du om det finns någon poäng med att lära sig grunderna i algebra?
Om du svarade ja på någon av dessa frågor så ska du veta att du inte är ensam, men också att du inte behöver oroa dig: Superprof är här!
En orsak till att elever ogillar algebra så mycket är att de inte riktigt vet vad det innebär. Dessutom är de osäkra på vad de ska göra. Även om ett av de bästa sätten att lära sig algebra på är genom att ta hjälp av en skicklig handledare så kan en ordentlig definition också hjälpa till att öka förståelsen för detta matematiska koncept.
En enkel definition av algebra är att det är en del av matematiken där bokstäver och symboler används för att representera antal samt mängd inom formler och ekvationer. Låter det inte särskilt spännande?
Låt oss berätta mer: Precis som meningar kan beskriva relationerna mellan olika ord så kan algebraiska ekvationer beskriva relationerna mellan olika variabler. Algebra kan ses och förstås som en dialekt inom det matematiska språket.
Algebra uppfanns ursprungligen för att göra livet lite enklare för alla som sysslar med matematik, vilket strider mot den allmänna uppfattningen att den skapades för att plåga elever! Det är också värt att nämna att forskare och matematiker har arbetat outtröttligt genom åren för att förenkla användningen av algebra.
Idag är det alltså lättare att lära sig grunderna i algebra än tidigare! Algebran är väldigt logisk och dessutom avgörande för att kunna få en ökad förståelse för mer komplex matematik.


Vad är linjär algebra?
För att bättre förstå definitionen av linjär algebra är det viktigt att analysera den gren av matematiken som handlar om linjära ekvationer. Så vad är linjära ekvationer?
En linjär ekvation är en ekvation som kan ställas upp i form av variabler och koefficienter som ofta är reella tal. En linjär ekvation ger dessutom en rak linje när den ritas in i en graf.
Så vad är därför linjär algebra? Linjär algebra handlar kort sagt om linjära kombinationer. Linjär algebra är studiet av linjer, vektorrum och matriser som behövs för linjära transformationer det finns mycket mattehjälp att få i Algebra.
Linjär algebra är viktig att förstå eftersom den är relevant inom många matematiska områden. Den är till exempel nödvändig inom geometrin; exempelvis för att definiera objekt som linjer och rotationer. Det är också viktigt att vara medveten om att linjär algebra används inom de flesta naturvetenskapliga samt tekniska områden.
Många erfarna matematiker anser exempelvis att det är omöjligt att utveckla en djupare förståelse för maskininlärning utan att känna till grunderna i linjär algebra. Linjär algebra är känd av många som datamatematik med matriser och vektorer som dataspråk.
Linjär algebra har också haft ett inflytande på statistiken. Linjär algebra ligger exempelvis till grund för matematiska verktyg så som Fourierserier och datorgrafik. Detta kanske låter riktigt klurigt, men snart kommer pusselbitarna att falla på plats.
Hur man förenklar algebra
Vad är egentligen svårast: att försöka läsa sanskrit eller att förstå en algebraisk ekvation? Även om båda är komplicerade uppgifter så skulle de som föraktar matematik välja att försöka sig på allt annat än att lära sig grunderna i algebra, det finns mattehjälp på nätet man kan få inom Algebra.
Men skulle du tro mig om jag säger att det finns knep för att göra algebra lite enklare? Eftersom algebra har funnits väldigt länge har det som sagt skett många förbättringar och justeringar för att förenkla den.
Matematiker vill att algebran ska vara så enkel och effektiv som möjligt att använda. För att lösa algebra på det "enklaste sättet" måste den alltså skrivas på ett så kompakt och effektivt sätt som möjligt, utan att uttryckets värde ändras på vägen. Den mest grundläggande regeln för att förenkla algebraiska uttryck är att veta att man kan addera lika termer.
Vad är lika termer?
Lika termer är termer som innehåller samma variabler: deras enda skillnad kan vara att koefficienterna ändras. För att effektivt förenkla algebraiska uttryck kan du testa att följa dessa steg:
- Att kombinera lika termer kan vara till stor hjälp.
- Ta bort parenteserna.
- Ta bort tecken så som minustecken.
För att förenkla algebraiska uttryck på ett korrekt sätt är det viktigt att utföra de olika stegen i rätt ordning. Detta är den ordning som gäller:
- Parenteser
- Potenser
- Multiplikation och division (från vänster)
- Addition och subtraktion (från vänster)
Om du är osäker på vissa regler vad gäller grunderna i algebra kan du överväga att ta hjälp av olika online-resurser för algebraövningar, eller av en handledare i matematik.
Faktorisering av algebra
Matematik är en komplett akademisk disciplin som bygger på en hel rad olika apsekter, koncept och begrepp. Faktorisering är en av alla viktiga matematiska aspekter. Det kan beskrivas som en handling för att hitta uttryck som sedan ska multipliceras för att skapa ett tal eller en ekvation.
Faktorisering är en viktig färdighet för den som vill lära sig grunderna i algebra och kunna lösa algebraiska problem på ett effektivt sätt. Genom att faktorisera kan man upptäcka eller eliminera möjliga svar mycket snabbare.
När du faktoriserar tal eller grundläggande algebraiska uttryck måste du ha koll på de följande tre stegen:
- Förstå hur faktorisering fungerar när det tillämpas på enstaka siffror.
- Kom ihåg att variabeldeklarationer också kan faktoriseras.
- Tillämpa multiplikationens distributiva egenskap.
Kom dock ihåg att det finns andra specifika steg att följa om matteuppgifterna istället skulle beröra faktorisering av kvadratiska ekvationer.

Vikten av att lära sig algebra
Om du vill lära dig mer om algebra kan du spana in vår guide om algebra för nybörjare. Om du fortfarande inte är övertygad om hur viktigt och användbar algebra är så kan du även kika närmare på de följande punkterna.
Här kommer ytterligare en del intressant fakta om fördelarna med att lära sig grunderna i algebra:
- Effektivare: Många elever som kämpar med matematik inser inte att deras förståelse för matematiken kommer att förbättras genom att lära sig algebra. Algebra gör det enklare att beräkna variabler än andra metoder. Det öppnar dessutom upp helt nya områden för att lösa olika vardagsproblem. Att lära sig algebra är ett sätt att få bättre och mer effektiva studieresultat.
- Logiskt tänkande förbättras: Att lära sig algebra är förstås inte det enda sättet att lära sig logik på, men det är en viktig fördel eftersom logik och algebra går hand i hand. Genom att lära dig algebra kommer du alltså att utveckla ditt logiska tänkande vilket är användbart i alla situationer.
Sammanfatta med AI: